Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 35

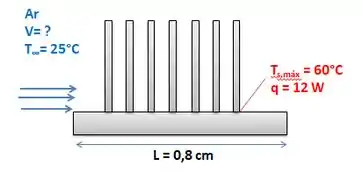
Um transformador de 10 cm de comprimento, 6,2 cm de largura e 5 cm de altura deve ser resfriado por meio de um dissipador de alumínio polido (emissividade = 0,03) de 10 cm x 6,2 cm de largura fixado na superfície superior. O dissipador tem sete aletas de 5 mm de altura e, 2 mm de espessura e 10 cm de comprimento. Um ventilador sopra ar a 25°C, paralelo às passagens entre as aletas.O dissipador deve dissipar 12 W de calor, e a temperatura da base do dissipador não deve exceder 60°C. Pressupondo que as aletas e a base sejam sejam quase isotérmicas e que a transferência de calor por radiação seja desprezível, determine a velocidade mínima de escoamento livre que o ventilador necessita fornecer para evitar superaquecimento.

Passo 1

Esse problema só parece assustar, mas basicamente o que ele tá pedindo é pra gente fazer o raciocínio contrário do que estamos acostumados! Se liga só...

Ele pede a velocidade, certo? E dentro dos problemas de convecção, em qual variável a gente consegue ver a velocidade do fluido? Reynold

Agora vamos lá, Reynold está sempre relacionado com outro número adimensional que é Nusselt que por sua vez está relacionado com h.

Ok! Mas o que então a gente tem que fazer? Vou te passar um fluxograma rapidinho de como fica a ideia desse problema.

E n c o n t r a r   h → c a l c u l a r   N u → C a l c u l a r   R e → E n c o n t r a r   V

Mas antes, vamos pegar as propriedades do fluido em Tf = 42, 5°C

K = 0,027   W / m . K

v = 1,7   x   10 - 5   m ² / s

P r = 0,72 5

Passo 2

Se ligou que ele deu um problema com aletas, certo? Então você deve estar já desesperado achando que vamos ter que fazer todas aquelas contas do inferno, mas trago pra você boas novas de salvação... NÃO, não vamos precisar kkkkk

A única equação que vamos precisar usar aqui é essa:

q = ɳ h A s T s - T ∞

h = q A s ɳ T s - T ∞

Mas aí vai dois pulos do gato, você tem que lembrar que esse As é área TOTAL de troca térmica, ou seja, devemos calcular a área de base não aletada e a área superficial das aletas, e que quando ele diz que as aletas podem ser consideradas isotérmicas, ele está dizendo que é uma aleta ideal e portanto sua eficiência ɳ é igual a 1, show?

A s = A s u p e r f .   l a t e r a l   d a   a l e t a + A b a s e   n ã o   a l e t a d a

A s u p e r f .     l a t e r a l   d s   a l e t a = 2 L a l e t a x   H a l e t a   x   N a l e t a

A s u p e r f .   l a t e r a l   d a     a l e t a = 2   x   0,005   x   0,1   x   7 = 0,007   m ²

OBS: A gente despreza á área relacionada a Haleta x taleta, onde taleta = espessura, porque essa área vai ser muito menor quando comparada a área da superfície lateral

A b a s e   n ã o   a l e t a d a = A b a s e - N a l e t a A b a s e   d a   a l e t a

A b a s e   n ã o   a l e t a d a = 0,1   x   0,062 - 7   x   0,002   x   0,1 = 0,0048   m ²

Logo, A s = A s u p e r f .   l a t e r a l   d a   a l e t a + A b a s e   n ã o   a l e t a d a = 0,007 + 0,0048 = 0,0118   m ²

Agora é só substituir os valores das variáveis:

h = q A s ɳ T s - T ∞ = 12 0,0118   x   1   x   60 - 25 = 29 ,   1 W m 2 ° C

Passo 3

Próximo passo é calcular Nusselt, se liga!

N u = h L K = 29,1   x   0,1 0,027 = 108,2

Passo 4

Agora vamos assumir que seja um escoamento laminar e usar a correlação para esse regime e considerando uma placa plana.

N u = 0,664   R e L 0,5 P r 1 3

R e L = N u 0,664   P r 1 3 2

Vamos abrir Reynold e isolar V

V L v = N u 0,664   P r 1 3 2 → V = v L N u 0,664   P r 1 3 2

V = 1 , 7   x   10 - 5 0,1 x   108,2 0,664   x   0,725 1 3 2 = 5,64   m / s

Resposta

V = 5,64   m / s  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita o problema 7-35 considerando que o dissipador foi pintado de preto e , portanto, tenha emissivdade efetiva de 0,9. Note que nos cálculos de radiação, está sendo utilizada a superfície da base (
92 - Uma placa de circuito com 0,5c m de espessura, 12c m de altura e 18c m de comprimento abriga 80 chips lógicos espaçados de um lado, cada um dissipando 0,06W . A placa é impregnada com recheios de
102 - Quatro transistores de potência, cada um com 10W de dissipação, são montados em uma fina placa vertical de alumínio k=237 W m ⋅ K com 22c m×22c m de tamanho.O calor gerado pelos transistores dev
76 -Em escoamentos através de bancos de tubos, por que o número de Reynolds é baseado na velocidade máxima em vez de na velocidade uniforme de aproximação?
75 – Em escoamentos através de bancos de tubos, como o coeficiente de transferência de calor varia de acordo com o número da fileira na direção do escoamento? Como varia na direção transversal para de