Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 91

A vazão da água através de um tubo com diâmetro de 10 cm deve ser determinada medindo a velocidade da água em diversos locais ao longo de uma seção transversal. Para o conjunto de medidas dadas na tabela, determine a vazão.

Passo 1

Antes de mais nada, a gente consegue perceber que a velocidade é uma função do raio, certo? Ou seja, temos V(r).

E quando temos isso, pra calcularmos a vazão, a gente pode fazer uma integral desse perfil na área transversal, correto?

MASSSSSS, aqui nesse caso não foi dado o perfil de velocidade, somente seus valores!

BUUUUUTTTTTTT, se você se lembrar bem de cálculo 1, qual é significado de integral? Nada mais é do que um SOMATÓRIO!

Q = ∫ V d A c ≅ ∑ V π ( r o u t 2 - r i n 2 )

Passo 2

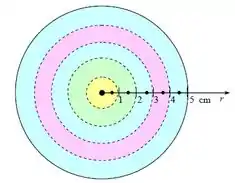
Ou seja, pra resolvermos esse problema a gente só precisa ficar somando o valor de velocidade em cada seção transversal, que seria a diferença de um raio maior e um raio menor.

Note que os pontos de medição são suficientemente próximos quepodemos dizer que a variação da velocidade entre um ponto e o seguinte, pode ser considerado linear.

Q = ∑ V π r o u t 2 - r i n 2 = π 6,4 + 6,1 2 0,01 2 - 0 + π 6,1 + 5,2 2 0,02 2 - 0,01 2 + π 5,2 + 4,4 2 0,03 2 - 0,02 2 + π 4,4 + 2 2 0,04 2 - 0,02 2 + π 2 + 0 2 0,05 2 - 0,04 2

= 0,0297   m ³ / s

Resposta

Q = 0,0297 m³/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que os três tubos de ferro fundido do problema a seguir sejam conectados de modo que se encontrem suavemente no ponto B, como mostrado abaixo. As pressões de entrada 1, 2 e 3 são 200 kPa, 160
Uma seção de teste de um túnel de vento tem seção quadrada de 91 cm de lado com as seguintes propriedades de escoamento: V = 45,7m / s , pressão absoluta p = 103,4k P a e T = 20 ° C . O bloqueio da ca
Na figura a seguir todos os quatro tubos são de ferro fundido de 45 m de comprimento e de 8 cm de diâmetro e se encontram na junção a, fornecendo água a 20°C. As pressões são conhecidas nos quatro pon
Para o problema 6.133, considere que, por questões de espaço, estejamos limitados a um comprimento total do difusor de 9,1 m. Qual seria o ângulo e a altura do difusor e a pressão na saída para a máxi
As perdas localizadas em uma válvula, conexões, curvas, contrações e dispositivos assemelhados são normalmente modeladas como proporcionais aAltura total Altura estáticaAltura de velocidadeQueda de pr