5.23. Calcule a resultante de um par de velocidades, uma de 100 km/h para o norte, outra de 75 km/h para o sul. Calcule a resultante se ambas as velocidades forem para o norte. Resultante de dois vetores em ângulo reto um com o outro:
Passo 1
Beleza, vamos começar com o caso que uma delas aponta para o norte e a outra para o sul:
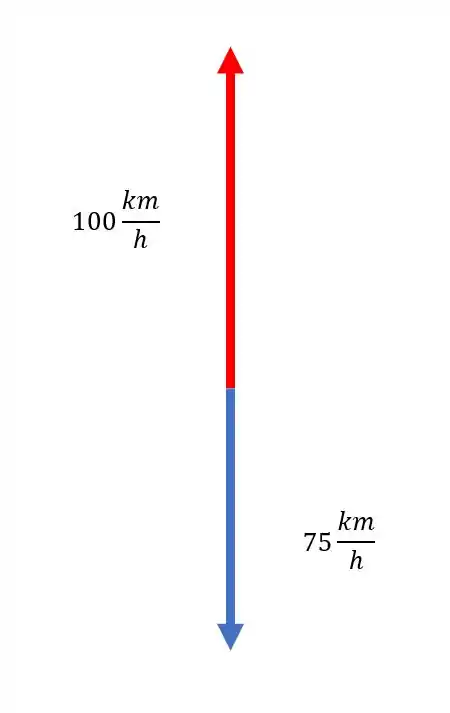
Temos dois vetores que estão na mesma direção, então a gente pode soma-los de forma simples, sem decompor nem nada, ambos estão no mesmo eixo.
Podemos assumir que o sentido norte é o sentido positivo. Então fica assim:
Como é positivo, aponta para o norte.
Passo 2
Agora os vetores continuam na mesma direção, então podemos continuar usando soma simples, mas agora um deles mudou de sentido, porque os dois apontam para o norte:
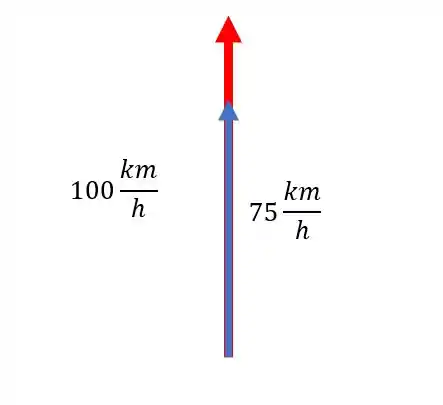
Então a resultante vai ser um vetor bem grande para o norte:
Apontando para o norte.
Passo 3
Finalmente vamos ver o que acontece se os vetores formarem um ângulo reto entre eles. Um ângulo reto é um ângulo de .
Bom, o enunciado já ajuda a gente bastante, porque aqui nós não podemos usar a soma simples, tem que ser uma soma vetorial, mas a gente já tem a formula:
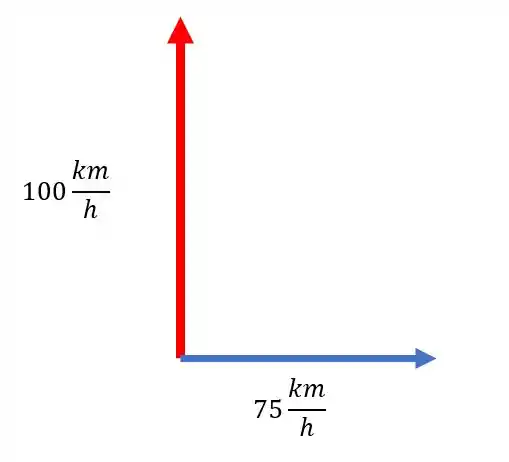
Então temos:
Até aqui tudo bem, mas para onde esse vetor aponta? Para descobrir isso podemos usar a regra do paralelogramo:
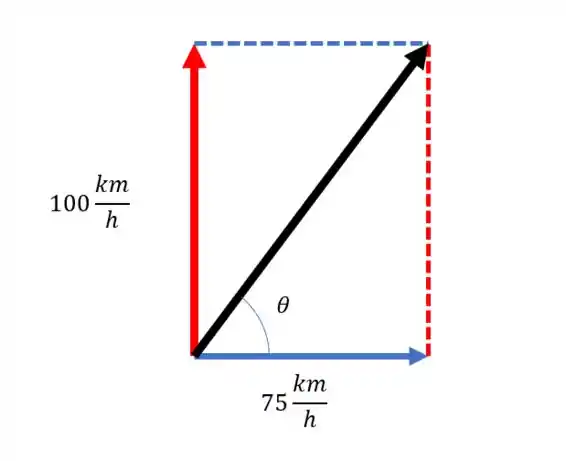
Aquele ângulo pode ser calculado com um pouquinho de trigonometria. A gente tem um triângulo, e seus catetos são e . Então:
Então
Podemos dizer que o vetor aponta a 52,77° acima do eixo oeste-leste.
Resposta
Para o norte.
Para o norte.
52,77° acima do eixo oeste-leste.