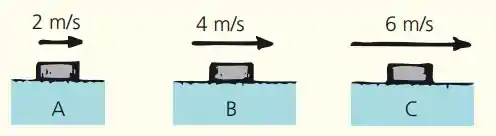
5.33. Três discos de hóquei idênticos, A, B e C, deslizam no gelo com determinadas velocidades. A força de arraste do ar e a de atrito com o gelo são desprezíveis.
a. Ordene os discos de acordo com a força necessária para mantê-los em movimento, em ordem decrescente de valor.
b. Ordene os discos de acordo com a força necessária para pará-los, em ordem decrescente de valor.
Passo 1
Vamos começar pelo item (a).
Nesse item a gente pode usar a primeira lei de Newton, o disco em movimento tende a manter seu estado de movimento se não houver forças para pará-lo, então, tudo que a gente precisa fazer para manter o disco em movimento é: NADA.
Essa aqui foi rápida, nenhum disco necessita de força para se manter em movimento, então a reposta é:
Passo 2
Agora vamos para o item (b), essa vai ser um pouco mais complexa.
Para parar o disco precisamos desacelerar.
Bom, a gente sabe que todos os discos tem massa igual, e a gente sabe também a velocidade deles. Olha só, com a velocidade a gente pode calcular o valor da aceleração para que ele pare:
Aqui, a gente vai supor que o tempo é igual para os três casos, para simplificar tudo a gente pode assumir que . E como queremos que ele pare . Então, para cada caso temos:
(A):
(B):
(C):
Passo 3
Agora que a gente calculou uma aceleração, e sabemos que todas as massas são iguais, podemos comparar as forças:
Olha só, a gente pode pegar só o módulo da força, não precisa se preocupar com o sinal, já que todas as forças estão no mesmo sentido:
Como todas as massas são iguais, só depende da aceleração, ou seja, só depende da velocidade. Quanto mais rápido o disco está, mais força para pará-lo, então a ordem fica a seguinte: