5.32. Cada uma das caixas é puxada pela mesma força F orientada para a esquerda. Todas as caixas possuem a mesma massa e deslizam sobre uma superfície sem atrito. Ordene em ordem decrescente em valor as seguintes grandezas:
a. As acelerações das caixas
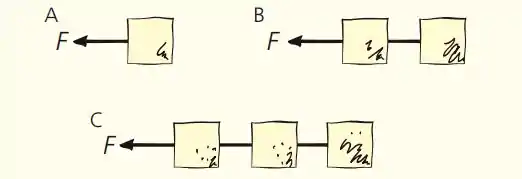
b. As tensões nas cordas presas a uma única caixa nas figuras B e C
Passo 1
Beleza, vamos começar pelo item (a).
A gente sabe que a força é sempre , e cada caixa tem massa .
Conseguimos calcular a aceleração pela segunda lei de Newton:
O caso (A) vai ser o seguinte:
Agora, no caso (B), temos duas caixas, então fica o seguinte:
É interessante aqui notar que as caixas vão ter sempre a mesma aceleração. Olha só, a força puxa a primeira caixa, e a primeira caixa puxa a segunda com a mesma intensidade, então, não é possível que uma caixa acelera mais que a outra.
Finalmente o caso (C):
Passo 2
Agora que a gente sabe a aceleração de cada caso, podemos ordenar. Olha só, quanto mais caixas tem o sistema, maior fica o denominador da fração que calcula a aceleração, isso significa que quanto mais caixas, maior a massa e por tanto menor a aceleração, então a resposta do item (a) fica:
Passo 3
Vamos para o item (b), calcular as tensões.
Aqui a gente vai usar a terceira lei de Newton, olha só, a caso (B) fica mais ou menos assim:
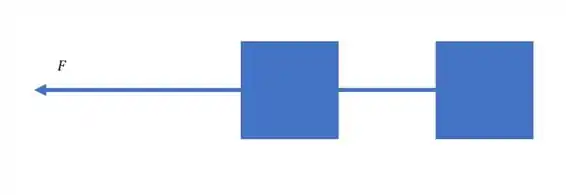
A caixa da frente vai exercer uma tensão na corda que puxa a caixa de trás. Mas a caixa de trás vai responder com uma força igual e oposta na corda, e vai exercer uma tensão na corda que vai puxar a caixa da frente:
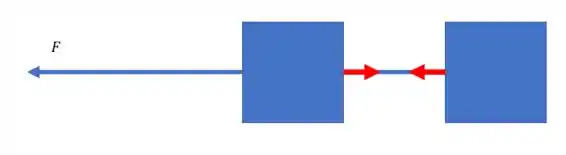
Então, a força resultante no sistema todo é só a força .
Já no caso (C) temos mais uma caixa:
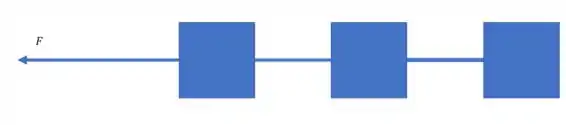
A gente pode seguir o mesmo raciocínio para encontrar a tensão na corda que prende as duas primeiras caixas:
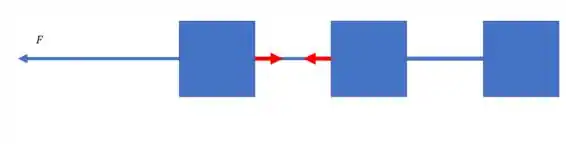
Agora as duas últimas caixas não vão mudar muito, olha só, a caixa do meio sobrou com a força resultante igual a , então, vai puxar a corda com a mesma força, e consequentemente puxa a última caixa. Por sua vez, a última caixa vai exercer uma força de reação na corda, e puxa-la com a mesma intensidade, e ficamos assim:
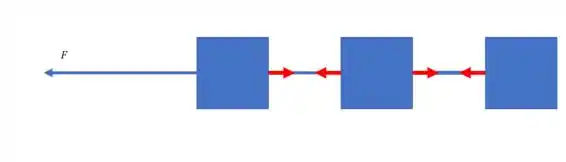
Então podemos dizer que os casos (B) e (C) são iguais nesse quesito, logo a resposta do item (b) fica: