Caixotes de massas variadas encontram-se sobre uma mesa nivelada e desprovida de atrito. Ordene-as em ordem decrescente quando aos módulos:
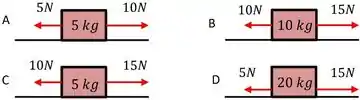
- das forças resultantes sobre os caixotes.
- das acelerações dos caixotes.
Passo 1
Opaaa tudo certo?
Bora lá pra mais uma seção! Agora vamos analisar casos diferentes e ordená-los de acordo com o que o autor pede.
Passo 2
- Podemos calcular as forças resultantes para cada módulo, onde a força positiva é considerada para a direita:
Então as forças resultantes sobre os caixotes, em ordem decrescente quanto aos módulos é
Passo 3
Então acelerações dos caixotes, em ordem decrescente quanto aos módulos é