O comprimento de onda da radiação emitida por um íon de hélio é praticamente igual ao da linha (a primeira linha da série de Balmer).
a) Entre quais estados (valores de ) ocorre a transição no íon de hélio?
b) O comprimento de onda é maior ou menor do que o da linha ?
c) Calcule a diferença entre os comprimentos de onda.
Passo 1
Fala galerinha, beleza?
A seguir reproduzimos todos os decaimentos envolvendo os quatro primeiros níveis de energia do átomo de hidrogênio:
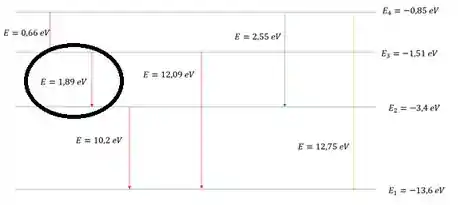
A transição destacada corresponde a linha : a transição de menor energia na série de Balmer (que termina em ).
Já para o átomo de hélio ionizado (), os níveis de energia são dados por
A “dedução” dessa expressão é explicada no problema 26 desse capítulo.
Desta forma, o fóton emitido em uma transição do átomo de hélio ionizado tem energia dada por
Queremos achar e tais que
Assim,
Vou deixar você brincar um pouco...
Brincou? Bora para a resposta: e satisfaz muito bem a relação!
Passo 2
Vamos calcular a energia exata dessa transição no hélio ionizado:
É quase igual a linha ! Observe que a energia é um pouquinho menor, isso faz com que o comprimento de onda seja um pouquinho maior!
A diferença entre os comprimentos de onda é dada por
Usando :