Um tubo de descarga de gases contém íons e átomos de , , , , e (o índice superior dá a massa atômica), com os quatro últimos ionizados de modo forma que tenham apenas um elétron.
a) Quando o potencial ao longo do tubo é aumentado a partir do zero, quais seriam as primeiras linhas espectrais que apareceriam?
b) Dê, em ordem crescente de frequências, a origem das linhas correspondentes à primeira linha da série de Lyman do .
Passo 1
Fala galerinha, beleza?
Como foi discutido no problema anterior (problema 32), o espectro de energia é dado por
é o número atômico, é a massa reduzida e é a massa do elétron. Com isso, as linhas espectrais têm energia dada por
A massa reduzida é dada por
onde é o número de massa e é a massa do próton. Desta forma,
Ou ainda,
Na última passagem usei a aproximação , se . Desta forma, podemos escrever
Vamos olhar apenas para o fator :
Ele vai terminar quais são serão as primeiras linhas espectrais!
Passo 2
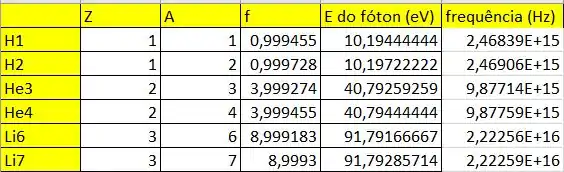
Na tabela a seguir apresentamos o valor de para cada átomo:
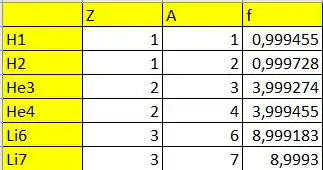
Vemos que o é predominante sobre o na determinação da escala de energia. Esperamos, em ordem crescente, que a linhas apareçam na seguinte ordem:
Passo 3
A primeira linha da série de Lyman ocorre com e , de modo que
Multiplicando pelos fatores de correção:
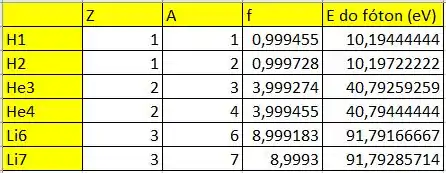
Para achar as frequências, basta lembrar que , de modo que
Usando , obtemos: