Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 15.Problemas - Ex. 59

Uma corda esticada está sobre o eixo O x . A corda é deslocada nos sentidos y e z , de modo que o deslocamento transversal da corda seja dado por

y x , t = A cos ⁡ ( k x - ω t ) z x , t = A sen ⁡ ( k x - ω t )

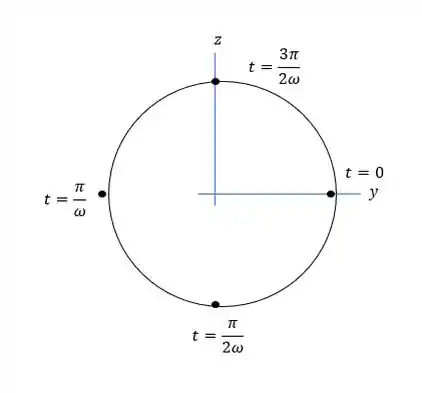
a)Faça o gráfico de z em função de y para uma partícula da corda em x = 0 .   Esse gráfico mostra a trajetória da partícula como vista por um observador sobre o eixo O x   olhando para x = 0 . Indique a posição da partícula em t = 0 , t = π \ 2 ω , t = π / ω e t = 3 π / 2 ω . b)Encontre o vetor velocidade de uma partícula em uma posição arbritária x sobre a corda. Mostre que esse vetor representa a velocidade tangencial de uma partícula que se desloca em um circulo de raio A com velocidade angular ω , e mostre que a velocidade da partícula constante (isto é, a partícula está em movimento circular uniforme). (Veja o Problema 3.75.) c) Encontre o vetor aceleração da partícula no item (b) . Mostre que a aceleração é sempre voltada para o centro do circulo e que o seu módulo é a = ω 2 A . Explique esses resultados em termos do movimento circular uniforme. Agora suponha que o deslocamento da corda fosse dado por

y x , t = A cos ⁡ ( k x - ω t ) z x , t = - A sen ⁡ ( k x - ω t )

Descreva como o movimento de uma partícula em x seria diferente do movimento descrito no item (a).

Passo 1

Bom galera,

y 2 x , y + z 2 x , y = A 2 .

A trajetória é um círculo de raio A.

Vamos recordar algumas derivações parciais:

v y = ∂ y ∂ t ,

v z = ∂ z ∂ t .

a y = ∂ v y ∂ t ,

a z = ∂ v z ∂ t .

Passo 2

  1. Em t = 0 : y 0,0 = A z 0,0 = 0 .

    2. Em t = π 2 ω : y 0 , π 2 ω = 0 z 0 , π 2 ω = - A .

    Em t = π ω : y 0 , π ω = - A z 0 , π ω = 0 .

    Em t = 3 π 2 ω : y 0,3 π 2 ω = 0 z 0 , 3 π 2 ω = A .

    A trajetória e esses pontos são esboçados na Figura a seguir:

    Passo 3

  2. Assim, para encontrarmos o vetor velocidade fazemos:

    3. v y = ∂ y ∂ t = + A ω s e n   ( k x - ω t )

    v z = ∂ z ∂ t = - A ω cos ⁡ k x - ω t .

    v → = v y j ^ + v z k ^ = A ω [ s e n   k x - ω j ^ - cos ⁡ ( k x - ω t ) k ^

    v = v y 2 + v z 2 = A ω

    então a velocidade é constante.

    r → = y j ^ + z k ^

    r → ⋅ v → = y v y + z v z = A 2 ω s e n k x - ω t cos ⁡ k x - ω t - A 2 ω cos ⁡ k x - ω t = 0 .

    r → ⋅ v → = 0 ,

    Então v → é tangente ao caminho circular.

    Passo 4

  3. E

a y = ∂ v y ∂ t = - A ω 2 cos ⁡ k x - ω t ,

a z = ∂ v z ∂ t = - A ω 2   s e n   ( k x - ω t )

r → ⋅ a → = y a y + z a z = - A 2 ω 2 [ cos 2 ⁡ k x - ω t + s e n 2   ( k x - ω t ) ] = - A 2 ω 2

Como r = A ,

r → ⋅ a → = - r a .

r → ⋅ a → = r a cos ⁡ ϕ

Então

ϕ = 180 °

E a → é o oposto na direção de r → ;

a → é radialmente para dentro.

Para esses y   ( x ,   t ) e z   ( x ,   t ) , y 2 + z 2 = A 2 , então o caminho é novamente circular, mas a partícula gira no sentido oposto comparado à parte (a).

Passo 3

A onda se propaga na direção +   x . O deslocamento é transversal, então v → e a → estão no plano y z .

Resposta

  2. v → é tangente ao caminho circular
  3. a → é radialmente para dentro
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seu primo Tobias está outra vez brincando com o varal do Exemplo 15.2 (Seção 15.3). Uma extremidade da corda do varal está presa a um poste vertical. Tobias segura a outra extremidade frouxamente na m
Um fio metálico com densidade ρ e Y , módulo de Young, é esticado entre dois suportes rígidos. Para uma temperatura T , a velocidade de uma onda transversal é igual a v 1 . Quando a temperatura aument
Uma corda de 50,0 cm de comprimento vibrando está sob uma tensão de 1,0 N. Os resultados de cinco fotografias estroboscopias sucessivas são mostradas na Figura 15.39. A taxa do estroboscópio é fixada
Uma onda senoidal transversal desloca-se em uma corda. A corda tem 8,0 m de comprimento e massa de 6,0 g. A velocidade da onda é 30,0 m/s e o comprimento de onda é 0,2 m.a) Se a onda deve ter uma pote
Uma corda de guitarra está vibrando em seu modo fundamental, com nós em ambas as extremidades. O comprometimento do segmento da corda que está livre para vibrar é 0,386 m. A aceleração transversal máx