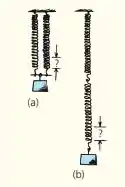
Uma determinada mola distende-se 4 cm quando uma carga de 10 N é pendurada nela. Quanto se distenderá a mola se uma outra mola idêntica sustentar essa carga junto com a primeira mola, para as situações mostradas em a e b? (Despreze os pesos das próprias molas.)
Passo 1
Fala galerinha. Tudo tranquilo? Espero que sim.
Nessa questão temos três situações. Primeiro, temos uma mola que se alonga quando tem uma força de sendo feita nela. Depois, temos que essa mesma força de é feita em duas molas, mas em uma situação (a) temos as molas em paralelo e em uma situação (b) elas estão em paralelo. Primeiro vamos achar a constante dessa mola e depois entender como fica essa associação de molas.
Passo 2
Pro primeiro caso, temos uma mola que sustenta uma carga que faz uma força de . Então vamos ter
Encontramos a constante da mola que vai ser usada. Agora vamos entender como fica quando fazemos a associação delas.
Passo 3
Quando as molas estão em paralelo, podemos ver que o deslocamento que uma tiver, a outra também vai ter. Assim, se o deslocamento da mola 1 for e o da mola 2 for vamos ter que
Esse é só um nome que colocamos pra ficar mais fácil já que esses deslocamentos são iguais.
Agora pensando na força resultante , vamos ter que
Como a equação da força é
Vamos ter que a força resultante vai ficar
Mas como vimos, o deslocamento de todos é igual. Então vamos ter
Dividindo todos por temos finalmente
Quando as molas estão em série.
Agora vamos resolver pro caso das molas em paralelo. Como foi usado molas iguais, vamos ter
Substituindo na equação que encontramos da constante da mola resultante, temos
Agora calculando quanto vai distender ou se alongar com a carga que faz a força de Só substituir na equação da força e fazer a conta.
A mola vai se distender ou alongar com as molas em paralelo.
Passo 4
Agora vamos ver como fica o caso em que as molas estão em série, ou seja, uma ligada na outra, que é o caso (b).
Primeiro, nesse caso, vamos ter que o que é igual nesse caso é a força. Então vamos ter
E temos também que o deslocamento das molas vai ser
Como a equação da força é
Então vamos ter
Mas como todas as forças são iguais, podemos colocar
E simplificando o vamos ter
Sendo essa a equação pra constante da mola no caso das molas em série.
Como novamente temos que as molas são iguais, vamos ter . Agora calculando o vamos ter
Invertendo os dois lados da equação vamos ter
Calculando o deslocamento, distensão ou alongamento da mola, temos
Então a mola vai se distender ou se alongar
Resposta
No caso das molas em paralelo, a mola vai se distender e no caso das molas em série, vai se distender .
Mais uma feita. Bora mais uma?