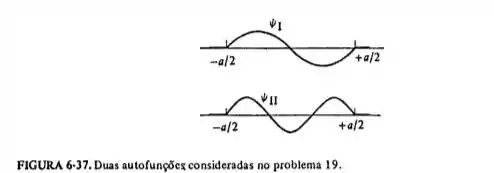
Duas autofunções possíveis de uma partícula se movendo livremente em uma região de comprimento , mas estritamente limitada a esta região, estão mostradas na figura 6-37. Quando a partícula estiver no estado correspondente à autofunção , sua energia total é . (a) Qual é sua energia total no estado correspondendo a ? (b) Qual é a menor energia total possível que a partícula neste sistema pode ter?
Passo 1
Fala galerinha, beleza?
O truque para resolver o problema é sacar que se trata de um poço infinito, cuja energia é dada por
Assim, tomando a razão entre as energias de dois níveis e :
Além disso, a autofunção correspondente a tem nós (pontos em que ela se anula). Assim, é fácil identificar para e para . Portanto,
Passo 2
O estado de mais baixa energia é tal que :