Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 120
Uma linha reta é traçada na superfície de um prato giratório de 16 cm de raio, do centro até a borda. Um besouro percorre esta linha a partir do centro, enquanto o prato gira no sentido anti-horário à taxa constante de 45 rpm. A rapidez do besouro em relação ao prato é constante, de 3,5 cm/s. Faça a orientação inicial do besouro coincidir com a orientação . Quando o besouro atingir a borda do prato (ainda viajando a 3,5 cm/s, radialmente, em relação ao prato giratório), quais são as componentes de e da velocidade do besouro?
Passo 1
Oi pessoal, vamos lá resolver esse problema? Primeiro nos foi dito que o besouro está em movimento e o prato também. Então trata-se de um problema de movimento relativo.
O problema que a velocidade do besouro depois de percorrer a linha feita no prato giratório. Então:
Onde:
Então o que ele quer é a velocidade do besouro em relação ao chão . Para acha-la, vamos precisar somar vetorialmente e .
Vamos começar encontrado o módulo velocidade da borda do prato em relação ao chão , porque já temos o módulo de . A gente quer a da borda porque é onde o besouro no instante onde queremos sua velocidade.
Sabemos que o prato gira à uma frequência de 45 rpm (rotações por minuto). Com a frequência podemos saber o período, pois a frequência é o inverso do período:
Para passar de minutos para segundos é só multiplicar por 60.
Aí para achar o módulo da velocidade do prato, a gente pode usar a fórmula da velocidade média:
Sendo que é o comprimento da borda do prato, então vai ser , sendo o raio do prato. E é o tempo decorrido em uma volta completa do prato, então é o período. Assim ficamos com:
ou
Passo 2
Agora temos que achar a forma vetorial das nossas velocidades. A velocidade da borda do prato é sempre tangente a essa borda, então a gente pode posiciona-la em qualquer ponto da borda. Inicialmente, temos algo assim:
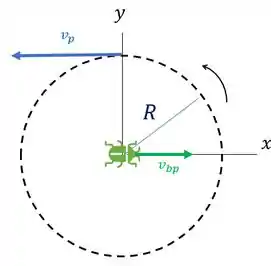
Só que isso é inicialmente. Precisamos saber como é a inclinação da direção do besouro quando ele está na borda do prato. Para montar nossos vetores em relação aos eixos coordenados.
Sabemos que ele andou na velocidade de . E andou até a borda do prato. Então ele andou a . Quanto tempo ele andou? Vamos usar a expressão da velocidade média novamente:
Agora a gente precisa saber quantas voltas nosso prato deu dentro desse tempo. A gente sabe que o prato dá uma volta em . Então, a gente pode dividir um tempo pelo outro:
Ele deu 3 voltas completas, e depois deu de uma volta no sentido anti-horário. Que ângulo é esse em relação a ?
Se uma volta completa é , podemos descobrir o ângulo que a gente quer pelo produto:
Então, quando o besouro está na borda, nossa situação está assim:
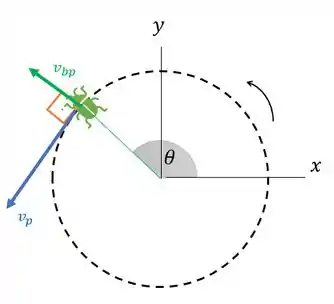
Passo 3
Como sabemos o ângulo podemos agora escrever nossas velocidades na forma vetorial. Vamos escrever a forma vetorial da velocidade do besouro em relação ao prato. Esse vetor verde
Obs: Pode ser que você ache valores um pouco diferentes mas isso ocorre por conta das aproximações. O princípio de resolução é o que vale.
Para a velocidade vetorial do prato (vetor azul) temos que:
Essa defasagem de se dá porque a velocidade que achamos para o prato era tangencial ao círculo. Assim a orientação dessa velocidade é mais , pois ela é normal a velocidade do vetor verde. Temos então que:
Passo 4
Finalmente podemos fazer a soma vetorial das velocidades que escrevemos no passo 1: