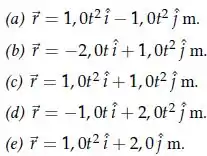Exercícios de Equações do Movimento em Notação Vetorial - Lista de Exercícios Resolvida

Um elétron de massa e velocidade horizontal incide em uma região entre duas placas paralelas eletricamente carregadas, conforme mostra a figura abaixo. Ao percorrer essa região o elétron é submetido a uma forca vertical , constante, para cima (sabe-se que ). Sabendo-se que o comprimento das placas é igual a e desprezando o efeito da aceleração da gravidade, determine:

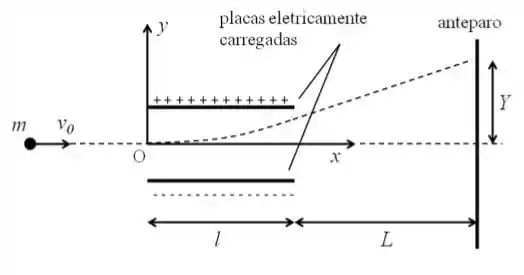
O vetor posição do elétron em função do tempo, quando este se encontra entre as placas paralelas eletricamente carregadas. Considere que a origem do sistema de coordenadas é do lado esquerdo das placas e que o elétron passa pela origem do sistema de coordenadas no instante , conforme mostra a figura. Expresse o resultado em termos de , , , e .

O valor de , quando o elétron atinge um anteparo situado a uma distancia das placas paralelas. Expresse o resultado em termos de , , , , .

Na figura abaixo, a partícula se move ao longo da reta com uma velocidade constante paralela ao eixo . No instante de tempo em que a partícula passa pelo eixo , a partícula deixa a origem com velocidade inicial zero e aceleração constante de módulo , o ângulo entre e o semi-eixo positivo é .

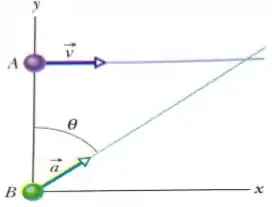
Escreva uma expressão para a velocidade da partícula .

Escreva uma expressão para a posição da partícula em função do tempo.

Escreva uma expressão para a posição da partícula em função do tempo.

Que valor de velocidade deve ter a particula para que aconteça a colisão?

Uma partícula deixa a origem com uma velocidade inicial e uma aceleração constante . Quando ela atinge o máximo valor de sua coordenada , quais são a sua velocidade e o seu vetor posição?

No tempo zero, uma partícula está em e e tem a velocidade . A aceleração da partícula é constante e dada por . Encontre a velocidade em Expresse o vetor posição em em termos de e . Além disso, dê a magnitude e a orientação do vetor posição neste tempo.

Um canhão dispara uma bala, desde o terraço de um edifício, na posição (unidades SI):

com velocidade inicial (unidades SI):

em que o eixo dos z aponta na direção vertical, para cima, e com origem no chão. Admitindo que a resistência do ar pode ser desprezada, calcule a altura máxima atingida pela bala e a posição em que a bala bate no chão.

Obs: Pega a calculadora que cê pode precisar ;)

As “lentes” de um microscópio eletrônico consistem em campos elétricos e magnéticos que controlam um feixe de elétrons. Como um exemplo da manipulação do feixe de elétrons, considere um elétron afastando-se da origem ao longo do eixo no plano com velocidade inicial . Sua aceleração pode ser decomposta em uma componente na mesma direção que a velocidade inicial, de módulo e outra no sentido perpendicular, com módulo .

Determine:

A expressão para a posição do elétron em função do tempo e a posição deste quando .

A expressão para a velocidade do elétron em função do tempo e a velocidade quando .

A velocidade escalar do elétron quando .

(d) A direção da trajetória do elétron.

Uma partícula, cuja velocidadeem t=0, sofre uma aceleração constante de módulo , que faz um ângulo com o eixo-x positivo. Qual é, aproximadamente, a velocidade em ?

Obs: Pega a calculadora que vai te ajudar :D

Um corpo encontra-se inicialmente (em unidades do SI) com velocidade . Em qualquer instante, a aceleração é dada pela expressão . Encontre a expressão para a velocidade em função do tempo.

As “lentes” de um microscópio eletrônico consistem em campos elétricos e magnéticos que controlam um feixe de elétrons. Como um exemplo da manipulação do feixe de elétrons, considere um elétron afastando-se da origem ao longo do eixo no plano com velocidade inicial . Sua aceleração pode ser decomposta em uma componente na mesma direção que a velocidade inicial, de módulo e outra no sentido perpendicular, com módulo .

Determine:

a) A expressão para a posição do elétron em função do tempo e a posição deste quando .

b) A expressão para a velocidade do elétron em função do tempo e a velocidade quando .

c) A velocidade escalar do elétron quando .

d) A direção da trajetória do elétron.

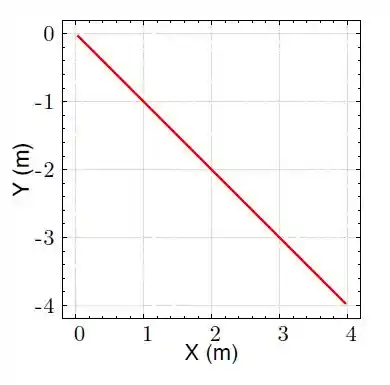
Uma partícula descreve uma trajetória dada por . Qual a expressão que descreve corretamente sua trajetória?

a)

b)

c)

d)

e)

(Cap 3 – Ex 52) Uma partícula tem uma aceleração constante No tempo t=0, a velocidade é zero e o vetor posição é . (a) Encontre os vetores velocidade e posição em função do tempo t. (b) Encontre a equação da trajetória da partícula no plano xy e esboce a trajetória.

(Cap 3 – Ex 110) Uma partícula se move no plano xy com aceleração constante.Em , a partícula está em , com a velocidade . Em , a partícula está em e com a velocidade . (a) Encontre . (b) Qual a aceleração da partícula? (c) Qual é a velocidade da partícula como função do tempo? (d) Qual é o vetor posição da partícula como função do tempo?

O vetor aceleração de uma partícula é dado por , onde e são constantes positivas. Sabendo-se que a velocidade da partícula em é igual a , com , determine

a) o vetor velocidade em função do tempo;

b) o instante de tempo em que os vetores velocidades e aceleração da partícula são ortogonais entre si.

Num laboratório, são lançados simultaneamente dois projéteis de dimensões desprezíveis.

No instante de lançamento, os projéteis ocupam as posições e , com e , de onde partem com velocidades e respectivamente. O sistema de eixos foi escolhido tal que .

(a) Os projéteis colidem em pleno voo? Se sim, em qual instante?

(b) Supondo que seja a altura inicial do primeiro projétil a partir do solo, quanto tempo ele leva para atingi-lo?

O vetor posição de um corpo em função do tempo, , é , onde (posição inicial), (velocidade inicial) e (aceleração) são vetores constantes. Afirma-se que: se e tem a mesma direção o movimento é retilíneo. a trajetória é um arco de parábola para qualquer . esta equação descreve um movimento circular uniforme. se o movimento é retilíneo e uniforme. A resposta correta é:

1. I e II estão corretas
2. I e III estão corretas
3. II e III estão corretas
4. I e IV estão corretas
5. Nenhuma delas esta correta

Considere o lançamento de projéteis num plano , onde o vetor aceleração pode ser escrito assim: Sobre o movimento do projétil, marque a alternativa incorreta:

(a) A velocidade do projétil ao longo da direção é constante;

(b) A aceleração do projétil ao longo da direção é zero;

(c) A velocidade do projétil ao longo da direção é constante;

(d) A aceleração do projétil ao longo da direção é ;

(e) A trajetória do projétil será uma parábola do tipo , onde , e são constantes.

O vetor velocidade (em ) de uma partícula é , onde e são os vetores unitários ao longo dos eixos e , respectivamente. Em que instante a partícula inverte o sentido do seu movimento?

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

O vetor posição de um corpo em função do tempo, , é dado por , onde os vetores (posição inicial), (velocidade inicial) e (aceleração) são constantes. Considerando a trajetória do corpo, qual a única incorreta das afirmativas a seguir?

(a) Se e tem a mesma direção o movimento é retilíneo.

(b) Se o movimento é retilíneo e uniforme.

(c) Se e o movimento é retilíneo uniformemente variado

(d) A trajetória descrita pelo corpo é uma parábola para qualquer valores de e .

Uma partícula move-se no plano , começando da origem em com uma velocidade inicial . Há uma aceleração dada por . O vetor velocidade num instante qualquer é:

a.

b.

c.

d.

e.

Duas partículas, e , se movem no plano com acelerações constantes iguais a e , respectivamente. A partícula inicia seu movimento na posição , com velocidade inicial de . A partícula começa o movimento na origem, partindo do repouso. Em que posição e em que instante de tempo as partículas de encontram?

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

O trem sai de uma estação a partir do repouso, rumo ao oeste, com aceleração constante de . Já o trem se move do norte para o sul com velocidade constante de , e passa por essa mesma estação segundos após a partida do trem . Considere o versos apontando para leste e o versor para o norte. Considere também a estação na origem do sistema de coordenadas, e considere o tempo inicial no instante em que o trem sai da estação.

Escreva uma equação cuja solução dê o instante de tempo em que a distância entre os trens é mínima (não precisa resolver). Essa distância mínima ocorre antes da passagem do trem pela estação? Justifique.

Sabendo-se que a posição de uma partícula, em relação à origem do plano , é determinada pelo vetor:

Com em metros () e em segundos (), determine:

O vetor velocidade instantânea e o vetor aceleração instantânea em função do tempo.

O vetor velocidade instantânea no ponto e o vetor aceleração instantânea no ponto , ambos os pontos estão indicados no gráfico abaixo. Neste gráfico, a curva contínua representa a trajetória da partícula, descrita através do vetor posição

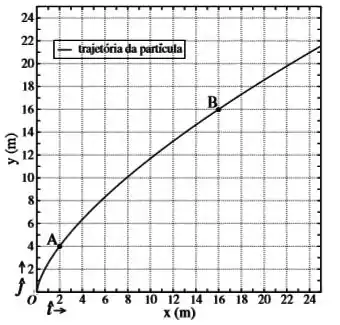
O vetor velocidade média e o vetor aceleração média , ambos entre os pontos e .

A posição de uma partícula em metros é descrita pelo vetor posição

O instante em que a partícula inverte o sentido do seu movimento é:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

A posição de uma partícula em metros é descrita pelo vetor posição

Seja o ângulo em radianos que o vetor velocidade da partícula faz com o eixo no instante . Pode-se afirmar que é igual a:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

O vetor velocidade de uma partícula é . Qual é o valor da aceleração no tempo ²

Na figura abaixo, a partícula se move ao longo da reta com uma velocidade constante paralela ao eixo . No instante de tempo em que a partícula passa pelo eixo , a partícula deixa a origem com velocidade inicial zero e aceleração constante de módulo , o ângulo entre e o semi-eixo positivo é .

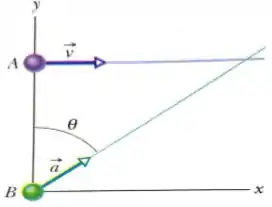
a) Escreva uma expressão para a velocidade da partícula .

b) Escreva uma expressão para a posição da partícula em função do tempo.

c) Escreva uma expressão para a posição da partícula em função do tempo.

d) Que valor de velocidade deve ter a particula para que aconteça a colisão?