Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.7 - Ex. 30
Ouvindo o ruído de uma serpente, você faz dois deslocamentos rápidos com módulos de 1,8 m e 2,4 m. Usando diagramas (aproximadamente em escala), mostre como esses deslocamentos deveriam ser efetuados para que a resultante tivesse módulo igual a:
a) 4,2 m
b) 0,6 m
c) 3,0 m
Passo 1
E aí, galerinha! 😊
Nesse problema temos que fazer a soma entre dois vetores de módulo e de modo que o vetor resultante tenha módulo a) , b) e c) .
Tem ideia de como fazemos isso? 😉
Bom, galera, vamos, primeiramente, relembrar algumas coisinhas para dar o “start” na nossa questão.
Os deslocamentos devem ser adicionados como vetores;
A magnitude da soma depende da orientação dos dois deslocamentos;
A soma de MAIOR magnitude acontece quando os dois deslocamentos são paralelos;
A soma de MENOR magnitude acontece quando os dois deslocamento são antiparalelos – ou seja, de direção oposta.
Para essa questão leve em consideração que só serão aceitos dois movimentos.
Veja só! 😎
Passo 2
- Aqui vamos ter os dois deslocamentos na mesma direção, ou seja, paralelos, basta soma-los para ter o resultado desejado.
- Já aqui temos dois deslocamentos em direções opostas, ou seja, antiparalelos, assim, calculamos a sua diferença.
- Agora, vamos seguir o mesmo raciocínio:
Ele afirma que o resultante é 4,2 m.
A somatória dos módulos dos vetores dados é
Logo, para somar vetores, eles devem ter a mesma direção e sentido.
No diagrama:
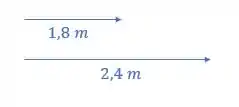
Logo,
Tranquilo até aqui? 😁
Passo 3
Ele afirma que o resultante é 0,6 m.
A diferença dos módulos dos vetores dados é
Logo, para subtrair vetores, eles devem ter a mesma direção mas sentidos opostos.
No diagrama:
Legal, né? 😉
Passo 4
Ele afirma que o resultante é 3,0 m.
Para fazer a escolha das orientações dos dois deslocamentos de tal forma que sua soma dê , essas tem que variar entre e . Logo, supondo que os movimentos sejam ortogonais:
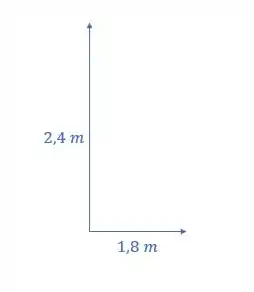
Basta fazermos a resultante da hipotenusa do triangulo retângulo:
E aí! entendeu tudo? Responde Aí! 😁