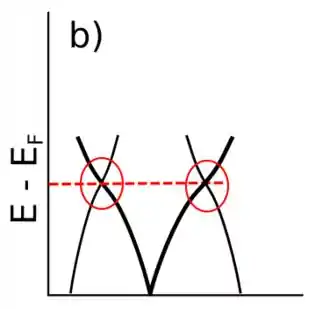
Parte do diagrama de 𝜀 em função de k para elétrons num supercondutor aparece mostrado na figura 14-14.
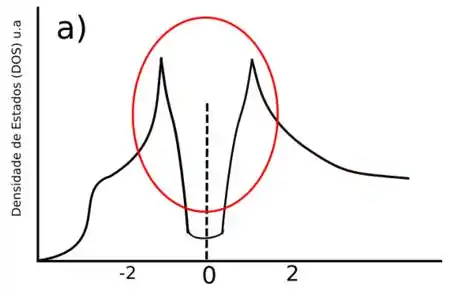
(a) Desenhe a curva da densidade de elétrons em função de 𝜀 para um supercondutor à T=0K.
(b) Desenhe um gráfico da energia necessária para criar buracos no estado de supercondutor e elétrons no estado normal. Este é um gráfico de () em função de se encontra no meio da banda proibida para semicondutor.
Passo 1
A densidade de estados para um supercondutor tem uma característica única. Uma vez que a dispersão eletrônica é “quebrada” a secção cruza a energia de Fermi em um arco (demarcada no círculo vermelho) no ponto zero, como veremos na figura que representará o item (a). Vale ressaltar que tanto o item (a) quanto o item (b) são gerados por meio de simulação em física computacional para nano estruturas.
Passo 2
O gráfico do item (b), acredito que seja uma relação do gap para energia de bandas desse estado (). Este gap é encontrado quando se resolve uma equação de onda para muitos elétrons, onde cada estado de energia degenerada gera bandas de valência e de condução. Um caso interessante é que, em supercondutores essas bandas apresentam uma característica chamada de Cone de Dirac. Esse efeito é bastante importante para a física computacional, o qual podemos observar características de material supercondutore na estrutura que estiver fazendo simulação.
Resposta