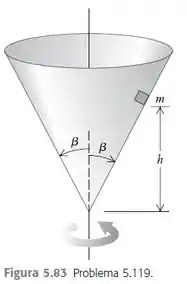
Um pequeno bloco de massa é colocado no interior de um cone invertido que gira em torno do eixo vertical de modo que o tempo para uma revolução é igual a (Figura ). As paredes do cone fazem um ângulo com a vertical. O coeficiente de atrito estático entre o bloco e o cone é . Para que o bloco permaneça a uma altura acima do vértice do cone, qual deve ser o valor máximo e o valor mínimo de ?
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que um pequeno bloco de massa é colocado no interior de um cone invertido que gira em torno do eixo vertical de modo que o tempo para uma revolução é igual a , conforme mostra a figura:
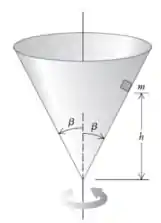
O coeficiente de atrito estático entre o bloco e o cone é .
Queremos calcular o valor máximo e o valor mínimo de para que o bloco permaneça a uma altura acima do vértice do cone.
Então... A ideia aqui é resgatar o resultado da velocidade máxima e mínima para uma bolinha de massa permanecer a uma certa altura que nem o exercício dessa mesma seção.
Passo 2
Se você passou reto por esse exercício, a gente chegou nesse resultado:
Para aceleração máxima temos que,
Para aceleração mínima,
Lembrando que a velocidade poderá ser calculada por,
Onde é a aceleração, é a aceleração da gravidade e é o raio.
Com esse resultado em mãos e lembrando que a velocidade é inversamente proporcional ao período, a gente pode encontrar as expressões para os períodos máximo e mínimo.
Mas calma, vamos por partes =)
Passo 3
Para resolver essa questão vamos relembrar da relação entre velocidade linear e período :
Tranquilo?
Agora vou fazer mais uma coisinha: vou relacionar a altura com o raio associado a essa altura, saca só no desenho:
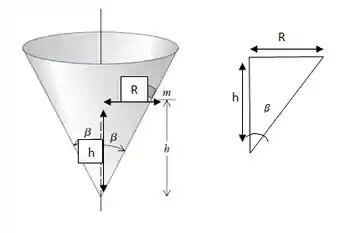
No nosso caso o raio pode ser relacionado com a tangente de e a altura :
E o período fica:
Passo 4
Agora relembrando do exercício onde foram encontrados os valores de máximo e mínimo das velocidades:
Passo 5
Sendo assim podemos relacionar o valor mínimo do período com o valor máximo da velocidade (já que eles são inversamente proporcionais):
Para o valor mínimo temos o máximo da velocidade:
Passo 6
E da mesma forma associar o valor máximo do período com o valor mínimo da velocidade:
Beleza?
Espero ter ajudado!
Vamos pra próxima?