Exercícios de Força Centrípeta - Lista de Exercícios Resolvida
Questão 1
Um carro pequeno de massa viaja em uma pista horizontal. Como ilustrado pela figura abaixo, em certa posição a pista possui um loop, uma circunferência vertical de raio :

Qual é a aceleração mínima, para que o carro, no topo do loop não perca o contato das suas rodas com a pista?
a) , com o sentido do vetor aceleração para baixo.
b) , com o sentido do vetor aceleração para cima.
c) , com o sentido do vetor aceleração para cima.
d) , com o sentido do vetor aceleração para baixo.
e) , com o sentido do vetor aceleração para cima.
Ver solução completaQuestão 2
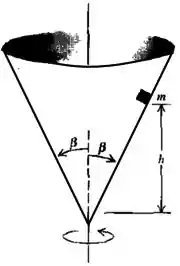
Um pequeno bloco de massa é colocado no interior de um cone invertido que gira em torno do eixo vertical. As paredes do cone fazem um ângulo com a vertical. O coeficiente de atrito estático entre o bloco e o cone é . Para que o bloco permaneça a uma altura acima do vértice do cone, qual deve ser o valor mínimo de ?
Questão 3
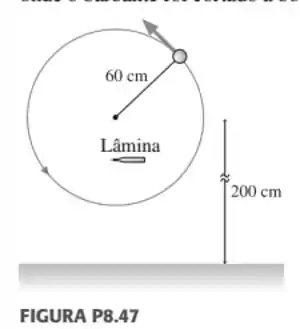
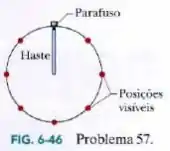
Um parafuso está enroscado em uma das extremidades de uma haste fina horizontal que gira em torno de outra extremidade. Um engenheiro monitora o movimento iluminando o parafuso e a haste com uma lâmpada estroboscópica, ajustando a frequência dos lampejos até o parafuso parecer estar nas mesmas oito posições a cada rotação completa da haste (Fig. 6-46). A frequência dos lampejos é por segundo, a massa do parafuso é e a haste tem de comprimento. Qual é o módulo da força exercida pela haste sobre o parafuso?
Questão 4
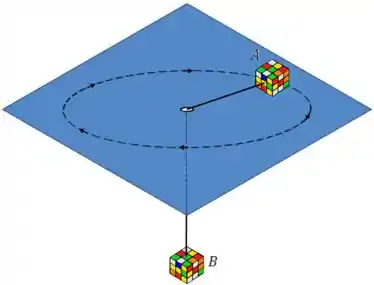
Um aluno, meio nerd, decide fazer uma experiência em uma mesa de ar. Ele solta um cubo de Rubik nessa mesa, preso por um fio que passar por um furo no centro da mesa, e na outra ponta do fio está outro cubo de Rubik, como mostrado na figura. Esse cubo sobre a mesa está realizando um movimento circular, de velocidade angular . Determine o raio do movimento considerando que o cubo pendurado está em repouso, e a massa de ambos os cubos é .
Questão 5
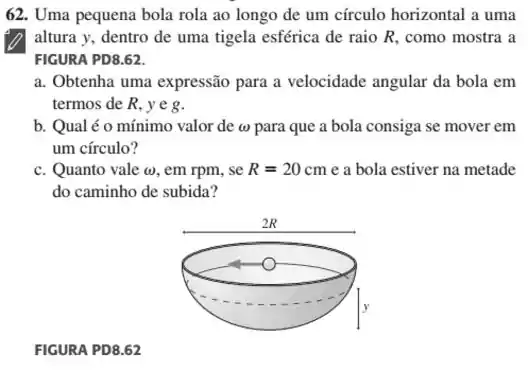
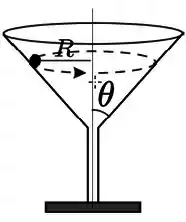
Uma partícula de massa está dentro de um funil de vidro e percorre a sua superfície inferior com um movimento circular uniforme horizontal. Não há atrito entre a parede do funil e a partícula. O ângulo que a parede do funil faz com o seu eixo de simetria é igual a , como mostra a figura. Desprezando a presença do ar, o módulo da força da superfície sobre a partícula e o módulo da aceleração centrípeta da partícula são, respectivamente,
- e
- e
- e
- e
- e
Questão 6
Os pneus de um carro de massa têm coeficiente de atrito estático com a pista horizontal de uma rodovia em uma curva circular de raio . A velocidade máxima com que o corpo pode fazer essa curva sem derrapar é . Supondo que o carro faça a curva com velocidade de módulo constante , podemos dizer que, nesse caso, a força de atrito estático entre os pneus e a pista tem módulo igual a
Questão 7
Dois corpos com massa e estão a uma distância e de um eixo. O corpo com massa está conectado por uma mola com constante elástica ao eixo e o corpo de massa está conectado ao corpo de massa por uma mola de constante elástica . Os corpos estão girando em torno do eixo com uma frequência angular , constante. Despreze as massas das molas e o efeito da aceleração gravitacional.
O que ocorre com o aumento gradual de ?
a) A mola entre os corpos sempre se rompe primeiro.
b) A mola entre o corpo e o eixo sempre se rompe primeiro.
c) A mola entre os corpos se rompe primeiro, se .
d) A mola entre os corpos se rompe primeiro, se .
e) Ambas, as molas, se rompem ao mesmo tempo.
Ver solução completaQuestão 8
Uma ambulância, de massa , está em uma estrada com velocidade constante, quando ele entra em uma curva de raio . Nesse momento ele percebe que o carro está na iminência de derrapar, porém mantém a velocidade constante na curva. Qual o valor do coeficiente de atrito da roda da ambulância com a estrada para ela conseguir fazer a curva?
Questão 9
Um bonde antigo, trafegando a , faz uma curva (plana) à direita com de raio. Neste bonde, existem alças de mão fixas ao teto, com liberdade para inclinar-se em qualquer direção.
c) Vistas por algum passageiro no fundo do bonde, em que direção as alças de mão se inclinam quando o bonde faz a curva? Justifique.
d) Qual é o ângulo que as alças de mão fazem com a vertical?
Ver solução completaQuestão 10
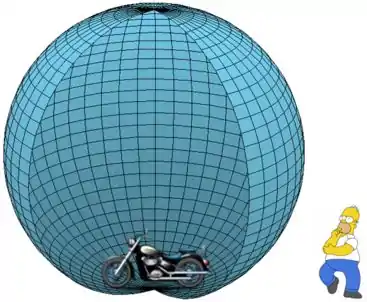
Homer, que possui massa , decide se aventurar no Globo da morte. Para isso ele deseja calcular a velocidade que ele pretende ficar para conseguir fazer o movimento. Como ele é “limitado” ele precisa da sua ajuda. Considerando que ele manterá uma velocidade constante , e o raio do Globo da morte é , e que o atrito neste caso é desprezível. Considere também que o módulo da aceleração da gravidade é . Determine
a) a força normal quando a moto passa na parte mais baixa do Globo.
b) a força normal quando a moto passa na parte mais alta do Globo.
c) a velocidade mínima para ele conseguir fazer a volta no Globo.
Questão 11
Em um dia gelado de inverno, o coeficiente de atrito entre os pneus de um carro e a estrada é reduzido a um quarto do seu valor em dia seco. Como resultado, a rapidez máxim na qual o carro pode percorrer com segurança a mesma curva de raio é igual a
reduzida de uma quantidade desconhecida que depende da massa do carro.
Ver solução completaQuestão 12
Você está dirigindo um carro em uma pista circular de raio , que é inclinada de um ângulo com a horizontal, como indicado na Figura. A velocidade do carro é , constante em módulo.
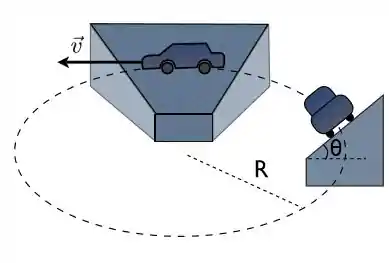
(a) Faça um diagrama de forças considerando que não existe nenhum tipo de atrito entre os pneus do carro e a pista.
(b) Calcule a velocidade na ausência de atrito em função de , e .
(c) Considerando que mesmo com o carro andando há uma força de atrito do tipo estático (de coeficiente ) entre os pneus do carro e a pista, que evita que o carro deslize para baixo ou para cima. Faça o diagrama de forças nestes dois casos.
(d) Com o atrito descrito no item (c) entre o pneu do carro e a pista, determine a velocidade mínima e máxima que o carro pode ter para que este não deslize.
Ver solução completaQuestão 13
Uma partícula de massa é suspensa por uma mola ideal de constante elástica presa no teto. A particula gira em movimento circular uniforme horizontal, de raio e centrado na vertical que passa pelo ponto de suspensão da mola no teto, como indica a figura. A mola mantém-se reta e distendida de um comprimento (a ser determinado). A reta que passa pelo ponto de suspensão da mola e a particual mantém um ângulo constante com a vertical, descrevendo uma superfície cônica no espaço. Considere como dados , , , e o módulo da aceleração da gravidade.
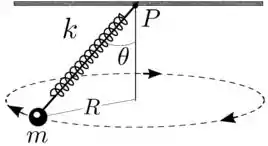
- Represente em um diagrama as forças que agem sobre a partícula em um instante arbitrário.
- Calcule a distensão da mola.
- Determine o módulo da velocidade da partícula.
Questão 14
Um corpo de massa é abandonado do alto de um plano inclinado (1), que possui altura em relação ao solo, e percorre seu comprimento livre de forças de atrito até entrar em um movimento de “loop” (2), conforme mostra a figura. Use para a aceleração da gravidade.
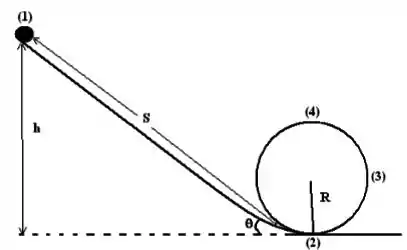
a) Utilizando um eixo de coordenadas com a direção paralela ao plano inclinado, represente o diagrama de corpo livre para a situação na qual o corpo se encontra na posição (1) e descreva, a partir da segunda lei de Newton, as componentes das forças que atuam no corpo para cada eixo.
b) Escreva a expressão para a velocidade em função da altura de lanamento com que o corpo chega à posição (2) indicada na figura.
c) Escreva a segunda lei de Newton por componentes para a situação na qual o corpo se encontra na posição (4) com velocidade e obtenha uma expressão para a altura mínima , em função do raio , de onde o corpo deve ser lançado para que consiga completar a volta no loop.
d) Considerando que o corpo abandonado de uma altura e o loop tem um raio , sua velocidade no ponto (3) é . Calcule os módulos e direções da força normal e da força resultante que atuam no corpo ao passar naquele ponto. Use .
Ver solução completaQuestão 15
Um pêndulo cônico é constituído por uma partícula presa a um fio ideal que faz um ângulo com a vertical, de modo que a partícula esteja em movimento circular uniforme em um plano horizontal com o centro da trajetória no ponto da vertical, como indica a figura. Em um dado instante, em que a partícula está em um ponto , sua aceleração é um vetor de
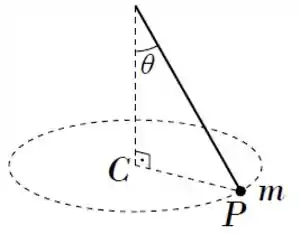
(a) módulo , vertical apontando pra baixo
(b) módulo , apontando de pra
(c) módulo , apontando de pra
(d) módulo , apontando de pra
(e) módulo , apontando de pra
Ver solução completaQuestão 16
Qual é o menor raio de uma curva sem compensação (plana) que permite que um ciclista a faça a curva sem derrapar se o coeficiente de atrito estático entre os pneus e a pista é de ?
Ver solução completaQuestão 17
A Fig. 6-18 mostra a trajetória de um carrinho de parque de diversões que passa, com velocidade escalar constante, por cinco arcos circulares de raios , e . Ordene os arcos de acordo com o módulo da força centrípeta que age sobre o carrinho ao passar pelos arcos, começando pelo maior.
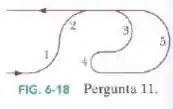
Questão 18
Numa estrada horizontal o módulo da velocidade máxima com que um carro pode fazer uma certa curva circular sem derrapar é igual a . Se num dia de inverno, em razão da presença de gelo na pista, o coeficiente de atrito estático entre os pneus do carro e a estrada fica reduzido à metade, o módulo da velocidade máxima com que o carro pode fazer a mesma curva sem derrapar é igual a
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 19
Uma partícula de massa está dentro de um funil de vidro e percorre a sua superfície inferior com um movimento circular uniforme horizontal. Não há atrito entre a parede do funil e a partícula. O ângulo que a parede do funil faz com o seu eixo de simetria é igual a , como mostra a figura. Desprezando a presença do ar, o módulo da força da superfície sobre a partícula e o módulo da aceleração centrípeta da partícula são, respectivamente,
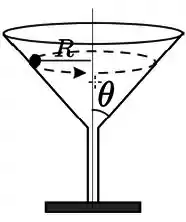
- e
- e
- e
- e
- e
Questão 20
Um carro realiza uma curva de raio em um plano inclinado sem atrito, de forma que o ângulo de inclinação do plano é suficiente para que o carro faça a curva sem subir ou descer no plano. Assinale a alternativa que corretamente relaciona o ângulo de inclinação com a velocidade do carro e o raio da curva:
a)
b)
c)
d)
e)
Ver solução completaQuestão 21
Suponha que o coeficiente de atrito estático entre os pneus de um carro de massa e a estrada onde ele trafega é
- Considerando que a pista é completamente plana, qual é a maior velocidade escalar com a qual o carro pode fazer uma curva de raio R sem derrapar (deslizar)?
Questão 22
Um disco horizontal, com um raio de roda em torno de um eixo vertical que passa pelo seu centro. O disco parte do repouso em e tem uma aceleração angular constante de . Em que instante de tempo as componentes radial e tangencial da aceleração linear de um ponto sobre a borda do disco serão iguais em magnitude?
a)
b)
c)
d)
e)
Ver solução completaQuestão 23
A posição de um helicóptero de treino de peso sob teste é dada por . Ache a força resultante que atua no helicóptero em .
Ver solução completaQuestão 26
Em um circo, um carro que faz acrobacias se aproxima de um loop de raio . Considerando que a partir do momento que entra no loop carro não acelera nem freia e que não há atrito durante este percurso, qual deve ser a velocidade mínima que o carro deve entrar no loop para conseguir realizá-lo por completo?
Questão 27
Em algum ponto da trajetória de determinada partícula, os vetores velocidade e aceleração são dados pelo diagrama abaixo.
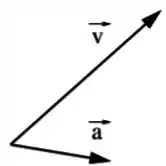
Dada a trajetória abaixo, determine que ponto da trajetória é compatível com este diagrama.
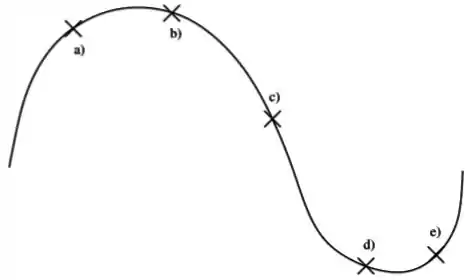
Questão 29
Um carro faz uma curva de raio numa pista plana (isto é, na figura) com atrito.
- Faça o diagrama das forças para o carro. Desconsidere a força de resistência do ar e as forças de atrito que retardam o movimento do carro.
- Encontre o coeficiente de atrito estático mínimo entre os pneus do carro e a pista, , para que o carro faça a curva com velocidade de módulo igual a .
- Considere agora que o carro faz uma curva de raio numa pista sem atrito e inclinada de um ângulo (vide figura). Faça o diagrama de forças e encontre o módulo da velocidade do carro, , neste caso.
- Se na situação do item o motorista aumentar o módulo da velocidade do carro para , o que acontece com o raio de curvatura da trajetória? Se houvesse atrito entre os pneus e a pista, para que lado apontaria a força de atrito neste caso? Repita o diagrama de forças incluindo a força de atrito.

Questão 30
Um disco de metal de massa está ligado a um cubo de massa através de um fio que passa por um furo no centro de uma mesa, conforme mostrado na figura.
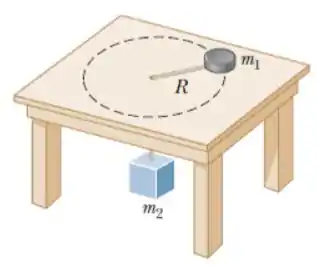
A superfície da mesa é perfeitamente lisa. O fio não tem massa e é inextensível. Considere . Você pode dar o resultado aproximado com uma casa decimal.
LEMBRETE: Todos os seus passos devem ser explicitados de forma clara.
- Suponha inicialmente que o movimento do disco é apenas radial, ou seja, na direção do fio. Qual será a aceleração do cubo? Você deve dar o módulo, a direção e o sentido do vetor aceleração.
- Ainda na situação de movimento apenas radial, determine a tração na extremidade do fio presa ao cubo?
- Suponha agora que o disco esteja descrevendo um movimento circular sobre a mesa ao longo de uma circunferência de raio . Qual deverá ser a velocidade do disco para que o cubo permaneça em repouso?
Questão 31
Duas pedras de massas idênticas são amarradas a cordas sem massa e postas a girar segundo trajetórias circulares horizontais com a mesma rapidez. O comprimento de uma das cordas é igual ao dobro do da outra. Qual é o valor da tração na corda mais curta em função da tração na corda mais longa?
(A) = /4
(B) = /2
(C) =
(D) = 2
(E) = 4
Ver solução completaQuestão 32
Você está dirigindo um carro em uma pista circular de raio , que é inclinada de um ângulo com a horizontal, como indicado na Figura. A velocidade do carro é , constante em módulo.
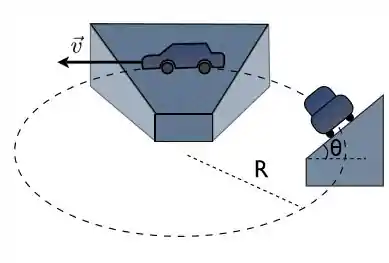
(a) Faça um diagrama de forças considerando que não existe nenhum tipo de atrito entre os pneus do carro e a pista.
(b) Calcule a velocidade na ausência de atrito em função de , e .
(c) Considerando que mesmo com o carro andando há uma força de atrito do tipo estático (de coeficiente ) entre os pneus do carro e a pista, que evita que o carro deslize para baixo ou para cima. Faça o diagrama de forças nestes dois casos.
(d) Com o atrito descrito no item (c) entre o pneu do carro e a pista, determine a velocidade mínima e máxima que o carro pode ter para que este não deslize.
Ver solução completaQuestão 33
Os satélites geoestacionários são aqueles que se encontram “parados” em relação a um ponto fixo na superfície terrestre (em geral, sobre a linha do equador terrestre). Por isso são usados como satélites de comunicação. Considere um satélite geoestacionário de massa com órbita circular de raio concêntrica com o globo terrestre. Adotando um sistema de referencial polar com centro no planeta Terra, determinar:
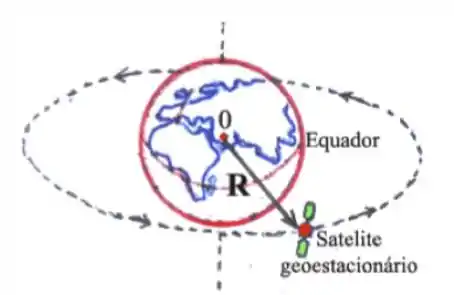
O período do movimento circular do satélite em segundos.
O raio da órbita circular em função do período do MCU (movimento circular uniforme), da massa da Terra, e da constante da gravitação universal, .
A velocidade escalar (ou módulo do vetor velocidade) em termos dos mesmos parâmetros da parte .
Ver solução completaQuestão 34
Um pequeno bloco com massa de está ligado a um fio que passa através de um buraco em uma superfície horizontal sem atrito (figura abaixo). Inicialmente, o bloco gira a uma distância de do buraco com uma velocidade de . A seguir, o fio é puxado para baixo, fazendo o raio do círculo encurtar para . Nesta nova distância verifica-se que sua velocidade passa para .
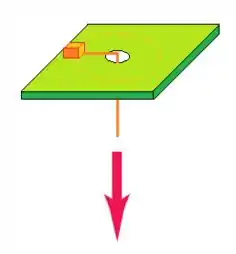
a) Qual era a tensão no fio quando o bloco possuía velocidade final ?
Ver solução completaQuestão 35
Um pequeno bloco com massa de está ligado a um fio que passa através de um buraco em uma superfície horizontal sem atrito (figura abaixo). Inicialmente, o bloco gira a uma distância de do buraco com uma velocidade de . A seguir, o fio é puxado para baixo, fazendo o raio do círculo encurtar para . Nesta nova distância verifica-se que sua velocidade passa para .
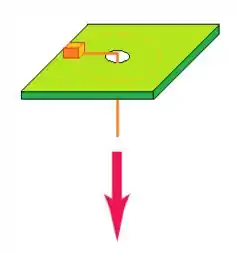
b) Qual era a tensão no fio quando o bloco possuía velocidade final ?
Ver solução completaQuestão 36
Uma vasilha de massa muito grande permanece sempre em repouso sobre uma mesa horizontal (a mesa não é mostrada na figura). A forma da vasilha é a de um tronco de cone circular reto com base de raio igual a e superfície lateral que faz um ângulo com a mesa. Deslizando por sua superfície interna sem atrito, um pequeno bloco de massa descreve um movimento circular uniforme de velocidade no sentido indicado pela flecha e sempre à mesma altura . No sistema de coordenadas mostrado, o plano - é horizontal e a gravidade é dada pelo vetor .
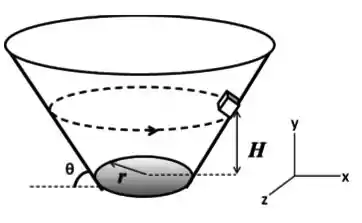
a) Num dado instante, a velocidade do bloco é dada pelo vetor . Represente o diagrama de corpo livre para o bloco nesse instante e desenvolva a segunda lei de Newton para cada um dos três eixos, , , . Encontre também o raio de curvatura da trajetória do bloco, em função de , e .
b) Considere , , , . Para uma trajetória do bloco com raio de curvatura , encontre o módulo da velocidade e o vetor que representa a força normal de contato exercida pela vasilha sobre o bloco.
c) Marque somente uma opção. Não é necessário justificar. No mesmo instante em que a velocidade do bloco é dada pelo vetor , a mesa exerce sobre a vasilha uma força total designada pelo vetor: . Sobre este vetor, é correto afirmar:
(i);
(ii);
(iii);
(iv);
(v);
(vi)
Ver solução completaQuestão 37
Um bloco 1 de massa é lançado de uma altura vertical ao longo de uma rampa e colide frontalmente com o bloco 2 de massa , que se encontrava em repouso na horizontal (veja a figura). Após a colisão, o bloco 1 retorna para a esquerda enquanto o bloco 2 sai para a direita, ambos com o mesmo módulo de velocidade, . O bloco 2 seguirá a trajetória entrando na pista semi-circular. Não há atrito dos blocos com o piso durante todo o percurso.
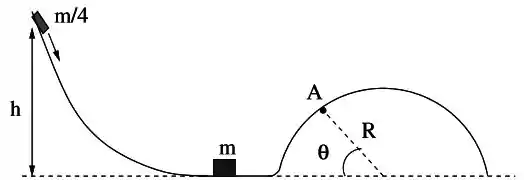
As respostas devem ser dadas em função dos dados que constam no desenho e/ou no texto acima, a saber: , , , e .
a) Ache a altura vertical máxima que o bloco 1 alcança após a colisão.
b) Ache a velocidade do bloco 1, , logo antes da colisão. Com isto, ache a velocidade original com que foi lançado, , quando partiu da altura .
c) Ache a velocidade com que o bloco 2 alcança o ponto , a um ângulo como mostrado na figura.
d) Ache o módulo da força normal sobre o bloco 2 em .
Ver solução completaQuestão 38
Em uma competição de uma olimpíada de inverno um esquiador de massa deve descer uma pista de neve em formato de de círculo de raio , como ilustrado ao lado. Sabendo que ele parte do repouso e que a razão entre o quadrado da sua velocidade e a altura é igual ao dobro da aceleração da gravidade , responda os itens abaixo em função de , e . Considere o atrito desprezível.
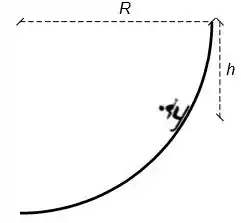
a) Faça um diagrama de corpo livre representando as forças que agem no esquiador, quando ele está à meia altura da pista.
b) Nesta posição, calcule o módulo da velocidade do esquiador e direção que ela faz com eixo vertical.
c) Ainda nesta posição, calcule o módulo da aceleração resultante.
d) Agora o esquiador chega no final da pista. Calcule nesta posição a força normal que a neve faz sobre ele.
Ver solução completaQuestão 39
Um passageiro de massa sentado em uma roda gigante se move com velocidade constante em uma trajetória circular de raio no plano vertical no sentido horário. Suponha que durante todo o movimento o passageiro está sempre sentado de cabeça para cima.
a) Faça um diagrama de corpo livre das forças que agem no passageiro no topo e no fundo da trajetória.
b) Escreva uma expressão literal para a diferença das forças normais que agem no passageiro nas duas posições. Como varia esta diferença em função da velocidade da roda gigante?
c) Suponha agora que no instante em que o passageiro alcança sua altura máxima, a força que age no assento aponta para baixo na direção vertical e tem módulo igual à do peso do passageiro. Para um raio igual a , calcule em quanto tempo a roda gigante dá uma volta completa.
Ver solução completaQuestão 40
Um disco de raio e massa e um cubo de lado e mesma massa, estão no topo de um plano com comprimento inclinado de com a horizontal. Existe atrito entre o plano inclinado e os dois objetos, os coeficientes de atrito cinético e atrito estático são respectivamente e . Na base do plano existe um trilho na vertical com o formato de um anel de raio como ilustra o desenho. A base do plano e o trilho têm superfícies com atrito desprezível. Na saída do trilho, está em repouso um segundo cubo idêntico ao primeiro com seu centro de massa na posição . Logo após o segundo cubo, a superfície horizontal apresenta um coeficiente de atrito cinético variável e no final desta superfície está uma mola com constante elástica . A superfície embaixo da mola tem atrito desprezível. A origem do sistema de coordenadas coincide com o centro do anel. A aceleração da gravidade é . Desenvolva as equações na forma literal para somente no final substituir as variáveis pelos valores fornecidos.
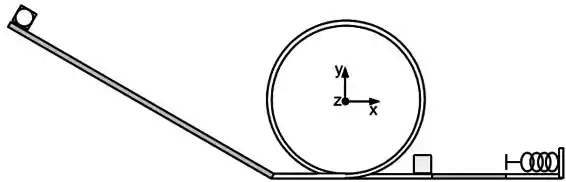
d) Um mecanismo segura o disco na base do plano e somente o cubo prossegue para fazer o percurso do trilho. Determine a aceleração total do cubo quando seu centro de massa está na posição . Suponha que na base do trilho a velocidade do cubo é de .
Ver solução completaQuestão 41
Um carro em um parque de diversões de parte do repouso do ponto A e se desloca sem atrito trilho abaixo em direção a um loop como mostrado na figura a seguir.
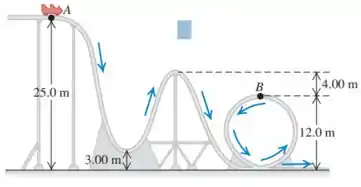
(b) Quão forte o carro pressiona o trilho no ponto B?
Ver solução completaQuestão 45
Dois pontos estão localizados sobre uma roda rígida que está girando com uma velocidade angular decrescente em torno de um eixo fixo. O ponto está localizado na borda da roda e o ponto está a meio caminho entre a borda e o eixo. Qual das seguintes afirmações referentes a esta situação é verdadeira?
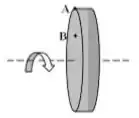
- Ambos os pontos possuem a mesma aceleração centrípeta.
- Ambos os pontos possuem a mesma aceleração tangencial.
- A velocidade angular no ponto é maior do que a velocidade angula no ponto .
- Ambos os pontos possuem a mesma velocidade angular instantânea.
- A cada segundo o ponto gira de um ângulo maior do que o ponto .
Questão 46
Uma partícula de massa é suspensa por uma mola ideal de constante elástica presa no teto. A particula gira em movimento circular uniforme horizontal, de raio e centrado na vertical que passa pelo ponto de suspensão da mola no teto, como indica a figura. A mola mantém-se reta e distendida de um comprimento (a ser determinado). A reta que passa pelo ponto de suspensão da mola e a particual mantém um ângulo constante com a vertical, descrevendo uma superfície cônica no espaço. Considere como dados , , , e o módulo da aceleração da gravidade.
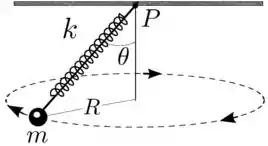
- Represente em um diagrama as forças que agem sobre a partícula em um instante arbitrário.
- Calcule a distensão da mola.
- Determine o módulo da velocidade da partícula.
Questão 47
Uma esfera muito pequena de massa está amarrada a uma haste vertical giratória por dois fios ideiais de comprimento . A haste gira de modo que os fios fiquem tensos formando com a haste um triângulo que mantem seu formato inalterado durante o movimento, conforme ilustra a figura. Sabendo que os fios de cima e de baixo fazem o mesmo ângulo com a horizontal e que a velocidade de rotação da esfera tem módulo constante , determine
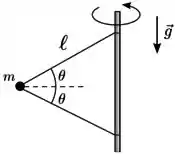
- O módulo e a orientação (direção e sentido) da força resultante sobre a esfera;
- O módulo da tensão no fio superior e o módulo da tensão no fio inferior;
- O limite mínimo do módulo da velocidade de rotação da esfera em torno da haste para que o fio inferior se mantenha esticado.
Questão 48
Um corpo de massa pendurado por um fio ideal de comprimento é abandonado de um ângulo a partir do repouso com o fio totalmente estendido, como mostra a figura. Sendo a tração no fio e o peso as únicas forças que atuam na massa , é correto afirmar que:
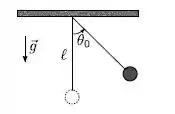
- No ponto mais baixo da trajetória
- O módulo da aceleração é constante
- No ponto mais baixo da trajetória,
- Para aceleração é nula.
- varia com o ângulo
Questão 49
Considere o pêndulo cônico mostrado na figura. Neste pêndulo, uma particula de massa m presa à extremidade de um fio ideal de comprimento l gira com velocidade angular constante ω, descrevendo um círculo de raio r. O módulo da tensão T no fio é:
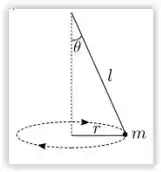
(A)
(B
(C)
(D)
(E
Ver solução completaQuestão 50
Qual é a força exercida pelo assento sobre um piloto de jato ao completar um loop vertical de de raio igual a 500 m a uma rapidez igual a 200 m/s? Admita que a massa do piloto seja igual a 70,0 kg e que esteja localizado no ponto mais baixo do loop.
(A) 4,90 x N
(B) 6,30 x N
(C) 700 N
(D) 660N
E) 8,40 x N
Ver solução completaQuestão 51
Um carro está se movendo numa pista circular horizontal de raio , com uma velocidade constante de . Um pêndulo simples está suspenso do teto do carro. Se o comprimento do pêndulo simples é pequeno comparado com as dimensões da pista, qual é o ângulo formado pela corda com a pista?
a) .
b) .
c) .
d) .
e) .
Ver solução completaQuestão 52
Uma partícula percorre uma trajetória circular de raio onde, no trecho do arco , o módulo da sua velocidade é reduzido uniformemente, isto é, com derivada constante. No ponto a sua velocidade é , conforme ilustrado na figura. Considere a sua aceleração decomposta segundo duas direções, um componente na direção radial (aceleração radial) e o outro componente na direção tangente à trajetória (aceleração tangencial). No seu movimento de para a afirmativa correta é
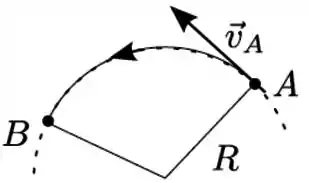
(a) a aceleração tem módulo constante;
(b) a aceleração radial tem módulo constante;
(c) a aceleração tangencial tem módulo constante;
(d) a aceleração tangencial é sempre nula;
(e) nenhuma das respostas anteriores.
Ver solução completaQuestão 53
(Cap 6 – Ex 60) A Fig. 6-53 mostra um pêndulo cônico, no qual um peso (pequeno objeto na extremidade inferior da corda) se move em uma circunferência horizontal com velocidade constante. (A corda descreve um cone quando o peso gira.) O peso tem uma massa de , a corda tem um comprimento e a massa desprezível e o peso descreve uma circunferência de . Determine (a) a tensão da corda e (b) o período do movimento.
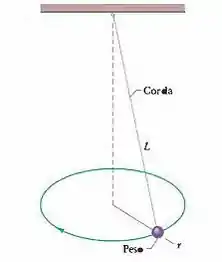
Questão 54
Um carro de corrida de massa igual a 500kg parte do repouso numa pista circular horizontal de raio igual a 400 m. Sua rapidez aumenta à taxa constante de 0.50 m/ .
(a) Explique e represente por meio de um desenho o que acontece com a direção do vetor aceleração à medida que a rapidez do carro vai crescendo.
(b) Quanto tempo levará até as magnitudes das acelerações radial e tangencial tornarem-se iguais?
(c) No instante do item (b), indique num desenho a direção e o sentido da força de atrito exercida pela estrada sobre o carro e determine sua a intensidade.
Ver solução completaQuestão 55
Um pêndulo cônico é constituído por uma partícula presa a um fio ideal que faz um ângulo com a vertical, de modo que a partícula esteja em movimento circular uniforme em um plano horizontal com o centro da trajetória no ponto da vertical, como indica a figura. Em um dado instante, em que a partícula está em um ponto , sua aceleração é um vetor de
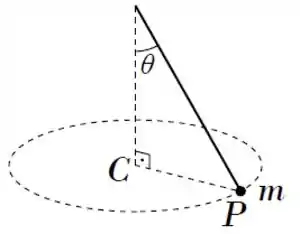
(a) módulo , vertical apontando pra baixo
(b) módulo , apontando de pra
(c) módulo , apontando de pra
(d) módulo , apontando de pra
(e) módulo , apontando de pra
Ver solução completaQuestão 56
Uma pequena bola de massa descreve uma circunferência num plano vertical presa a um fio de comprimento e massa desprezível (vide figura). A outra extreminade do fio (ponto da figura está presa a um dinamômetro (balança de mola) que registra a tensão no fio em cada instante. A tensão no fio é quando ele forma um ângulo de com a vertical.
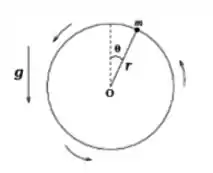
- Qual é a rapidez da bola quando ;
- Qual é o módulo da aceleração da bola quando .
Questão 57
Um carro de massa trafega com velocidade de módulo constante na direção leste inicialmente. Ele então entra numa curva de raio constante na posição da figura. No final da curva (posição ) o carro passa a trafegar na direção norte. O comprimento da curva é de . O carro completa o percurso da curva em . Os coeficientes de atrito estático e cinético entre os pneus do carro e o asfalto da curva são respectivamente e .
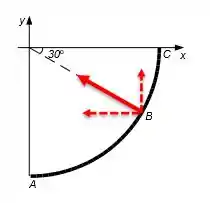
(a) Calcule a aceleração do carro quando ele está na posição em termos dos vetores unitários e .
(b) Calcule em termos dos vetores unitários e as forças de atrito que agem sobre os pneus do carro no início e no final da curva, posições e .
Ver solução completaQuestão 58
Um satélite se move, com rapidez constante, em uma órbita circular em torno da terra. Qual das afirmações abaixo sobre este movimento é correta:
(a) A aceleração e a velocidade do satélite apontam na mesma direção.
(b) A força resultante atuando sobre o satélite é nula.
(c) A velocidade do satélite é constante.
(d) Quando o combustível do satélite se esgotar, ele cairá na Terra.
(e) A aceleração do satélite aponta na direção da Terra.
Ver solução completaQuestão 59
A figura abaixo mostra um sistema composto por duas partículas, ambas com massa , conectadas por fios inextensíveis e de massas desprezíveis de comprimento cada.
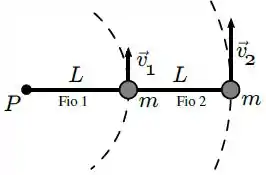
O fio está preso ao ponto fixo , enquanto o fio liga uma partícula à outra. O sistema gira em torno do ponto sobre uma superfície plana horizontal sem atrito, com velocidade angular .
Os módulos das velocidades e de cada partícula são constantes. e são as trações nos fios e respectivamente. Marque a alternativa correta:
Questão 60
. O coeficiente de atrito estático entre uma moeda e uma mesa que está rodando é . A
mesa roda a por minuto. Qual é a distância máxima a partir do centro da mesa que a
moeda não irá deslizar?
Ver solução completaQuestão 61
Parte de uma ferrovia é composta por dois trechos retilíneos mutuamente ortogonais conectados por um arco de circunferência conforme mostrado na figura abaixo. Uma locomotiva percorre a ferrovia no sentido do ponto ao ponto com velocidade de módulo constante.
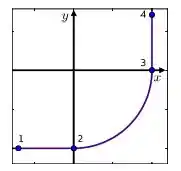
Considere, então, os trechos abaixo, em que o tempo é representado no eixo horizontal, enquanto no eixo vertical encontra-se alguma função de . Assinale a alternativa que lista corretamente os trechos correspondentes à componente da velocidade, à componente da velocidade, ao módulo da aceleração e à aceleração tangencial, respectivamente, da locomotiva em função de :
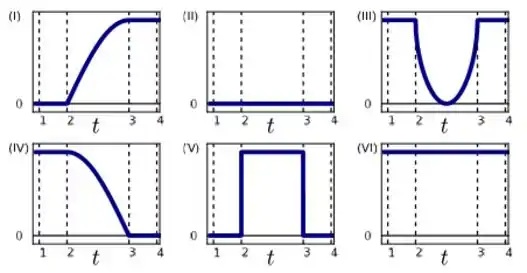
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 62
A força centrípeta é melhor explicada por qual das seguintes afirmações?
- A força centrípeta é a força resultante agindo sobre um objeto em órbita que o mantém em movimento circular.;
- A força centrípeta é a força dirigida ao longo de uma linha que é tangente à órbita;
- A força centrípeta é a mesma coisa que a força centrífuga: são sinônimos.
- A força centrípeta é uma força fundamental da natureza
- A força centrípeta é uma força dirigida radialmente para fora a partir do centro da sua órbita C.
Questão 63
Um carro de massa trafega pelo topo de um morro de raio de curvatura com uma velocidade de módulo constante , conforme a figura. Considere .
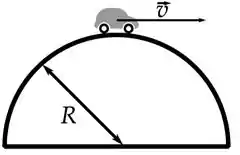
(a) Tratando o carro como uma partícula pontual e desconsiderando forças de atrito, represente diagramaticamente todas as forças que atuam sobre o carro quando ele está no topo do morro. Caso exista uma força resultante neste movimento, represente-a separadamente.
(b) Qual é o módulo da força normal que atua sobre o carro quando ele está no topo do morro a uma velocidade ?
(c) A que velocidade o carro está na iminência de perder o contato com o solo?
Ver solução completaQuestão 64
Uma pequena esfera metálica de massa está presa a uma corda de massa desprezível que gira num plano vertical num círculo de raio , como mostrado na figura. A velocidade da esfera no ponto mais baixo é de e a intensidade da força de tração na corda é de . Qual das alternativas abaixo mais se aproxima da massa da esfera metálica?
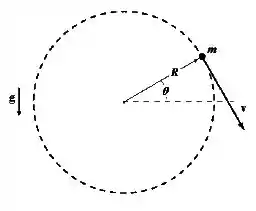
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 65
Um observador em repouso observa o movimento circular uniforme de um objeto sujeito a ação de apenas 2 forças. É correto afirmar que:
(a) Nenhuma das forças pode ter a direção tangencial.
(b) Uma das duas forças necessariamente aponta para o centro do círculo.
(c) As duas forças devem ser radiais e apontar para o centro do círculo.
(d) As duas forças devem ser radiais e pelo menos uma delas deve apontar para o centro do círculo.
(e) É possível que nenhuma das forças aponte para o centro do círculo.
Ver solução completaQuestão 66
Um viciado em movimento circular, com de massa, passeia em uma roda-gigante que descreve uma circunferência vertical de de raio a uma velocidade escalar constante de .
- Qual é o período do movimento?
Qual é o módulo da força normal exercida pelo assento sobre o viciado quando ambos passam
(b) pelo ponto mais alto da trajetória circular e
(c) pelo ponto mais baixo?
Ver solução completaQuestão 67
Um pêndulo cônico é constituído por uma partícula presa a um fio ideal que faz um ângulo com a vertical, de modo que a partícula esteja em movimento circular uniforme em um plano horizontal. O centro da trajetória está no ponto , como mostra a figura. No instante quando a partícula está em um ponto , pode-se afirmar que o vetor que representa a força resultante sobre a partícula
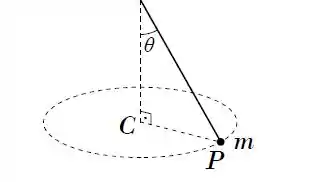
a) aponta de para .
b) aponta de para .
c) aponta para baixo.
d) aponta para cima.
e) tem a direção tangencial à trajetória circular.
f) tem a direção ao longo do fio.
Ver solução completaQuestão 68
Suponha que o coeficiente de atrito estático entre a estrada e os pneus de um carro é e não há sustentação negativa. Que velocidade deixa o carro na iminência de derrapar quando faz uma curva não compensada com de raio?
Ver solução completaQuestão 69
Um corpo de massa igual a está preso a um fio ideal. O corpo move-se ao longo de um círculo vertical de raio igual a sob a ação exclusiva da força gravitacional e da tensão no fio. O ponto A está localizado no topo do círculo, o ponto C está localizado no fundo do círculo. Os pontos B e D estão localizados exatamente a meio caminho entre os pontos A e C.
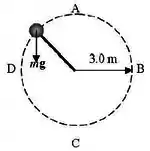
Qual das afirmativas abaixo é correta acerca da tensão no fio ?
(A) A tensão é menor no ponto A.
(B) A tensão é menor no ponto C.
(C) A tensão é menor nos pontos B e D.
(D) A tensão é a mesma nos pontos A e C.
(E) A tensão é a mesma em todos os pontos.
Ver solução completaQuestão 70
Um carro de massa descreve sem derrapar uma curva no plano horizontal de raio com velocidade . O gráfico ao lado indica o comportamento da força de atrito para este caso específico.
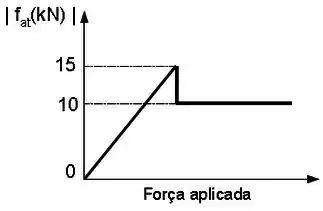
(c) Determine os coeficientes de atrito estático e cinético entre o carro e a pista.
Ver solução completaQuestão 71
Um carro de massa descreve sem derrapar uma curva no plano horizontal de raio com velocidade . O gráfico ao lado indica o comportamento da força de atrito para este caso específico.
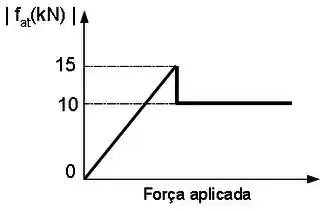
(a) Determine o módulo da força de atrito que atua no carro neste momento.
Ver solução completaQuestão 72
Para o pêndulo cônico ao lado, e a massa é .
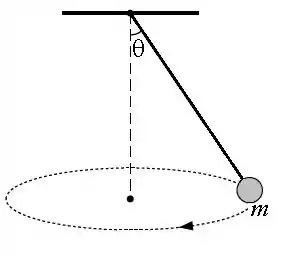
(a) Anote na figura as forças que agem no pêndulo.
(b) Escreva as equações que governam o movimento do pêndulo. Utilize um sistema de coordenadas em que um dos eixos aponte na direção do centro da trajetória.
(c) Determine o módulo da força resultante que atua no pêndulo.
Ver solução completaQuestão 73
Um disco está preso a um fio cujo comprimento é , e realiza um movimento circular sobre uma mesa de altura em relação ao solo. O fio arrebenta e o disco é lançado horizontalmente, atingindo o solo após um deslocamento horizontal de em relação ao ponto em que o disco deixa a mesa. Qual é o módulo da aceleração centrípeta do disco antes de o fio arrebentar? Despreze o atrito entre o disco e a mesa e use que .
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 74
Um “pêndulo cônico” é formado por uma bola de presa a um barbante de de comprimento, fazendo com que a massa se mova em um círculo horizontal com de raio. A figura abaixo mostra que, ao girar, o barbante descreve a superfície de um cone imaginário, daí o nome do dispositivo. Quanto vale a velocidade angular da bola?
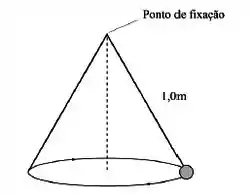
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 75
Um carro trafega com velocidade constante de módulo , numa estrada curva e inclinada de ângulo com a horizontal. A massa do carro é e o raio da curva é . A velocidade para se fazer a curva sem a ação do atrito é igual a . Os coeficientes de atrito estático e cinético entre os pneus e a estrada são respectivamente e . O desenho abaixo mostra uma vista frontal do carro e da curva inclinada.

Utilize: e .
(a) Faça o diagrama de corpo livre para o carro nesta situação sabendo que o carro faz curva com velocidade igual a . Utilize para a aceleração da gravidade.
(b) Utilizando notação literal, escreva a segunda lei de Newton na forma vetorial e por componentes para esta situação. Especifique as direções envolvidas na decomposição dos vetores.
(c) Sabendo que o módulo da força centrípeta que age sobre o carro nesta situação é igual a , calcule o módulo da força de atrito que age sobre o carro.
Ver solução completaQuestão 76
Um carro viaja com velocidade constante em uma pista circular horizontal. No diagrama abaixo, é a força de resistência do ar sobre o carro. Qual das outras forças mostradas melhor representa a força horizontal da pista sobre os pneus do carro?
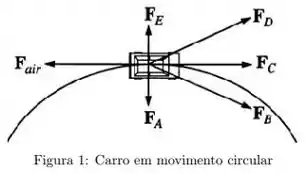
A.
B.
C.
D.
E.
Ver solução completaQuestão 77
Entradas e rampas de saída circulares em rodovias são frequentemente elevadas, para permitir que um veículo circule nelas com velocidade de até . Para projetar uma rampa semelhante que suporte uma velocidade de , deve-se:
A. aumentar o raio por um fator de ;
B. diminuir o raio por um fator de ;
C. diminuir o raio por um fator de ;
D. aumentar o raio por um fator de ;
E. aumentar o raio por um fator de ;
Ver solução completaQuestão 78
Você gira uma bola em círculos em um plano vertical, usando uma corda de comprimento . Existe uma velocidade angular mínima que você deve manter para que a bola execute o círculo completo. Se você girar a bola com velocidade angular menor do que , a corda fica frouxa e a bola não consegue chegar ao ponto mais alto do círculo. Qual o valor de em rpm?
Dados:
(A) rpm
(B) rpm
(C) rpm
(D) rpm
(E) rpm
Ver solução completaQuestão 79
Uma moeda de massa repousa sobre um bloco de massa . Ambos estão sobre uma plataforma circular de raio que gira com 60 rotaçoes por minuto em torno de um eixo na direção vertical. Os coeficientes de atrito estático e cinético entre o bloco e a plataforma são respectivamente e . O coeficiente de atrito estático e cinético entre a moeda e o bloco são respectivamente e . Use e .
Calcule as forças centrípetas que atuam na moeda e no bloco.
Faça um diagrama de corpo livre da moeda e do bloco e indique (se houver) os pares ação-reação.
Calcule a força de atrito que atua entre o bloco e a plataforma.
Qual é a máxima rotação por minuto que a plataforma pode ter antes que o bloco ou a moeda caiam da plataforma.
Ver solução completaQuestão 80
Ao passar pelo ponto mais baixo de um loop circular de uma montanha russa de raio , o peso aparente dos passageiros aumenta em em relação ao seu peso real. Quanto vale a velocidade do vagão nesse ponto?
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 81
O carrinho de uma montanha russa em um parque de diversões tem sua trajetória passando pela parte interna do círculo indicado na figura. Desconsidere o atrito entre o carrinho e o trilho da montanha russa. Sabendo que, se existirem, é a força peso que a Terra exerce sobre o carrinho, é a normal que o trilho exerce sobre o carrinho, é a força tangencial exercida pelo trilho e é a força centrípeta, qual das figuras a seguir indica corretamente as forças que atuam sobre o carrinho no instante em que ele passa pelo ponto ?
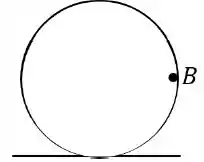
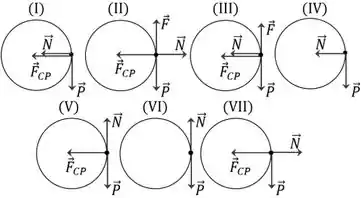
(a) Figura (I)
(b) Figura (II)
(c) Figura (III)
(d) Figura (V)
(e) Figura (VI)
(f) Figura (IV)
(g) Figura (VII)
Ver solução completaQuestão 82
A figura abaixo representa um disco de massa M homogêneo e uniforme, de espessura desprezível, e raio R. O disco gira no sentido horário em torno do seu eixo de simetria, com velocidade angular constante de módulo ω, e move-se sob a ação da força F mantendo-se sempre num mesmo plano. Sabendo-se que a aceleração do centro de massa do disco é devida apenas a ação da força F, o módulo da aceleração do ponto P localizado na borda do disco, mostrado na figura, é:
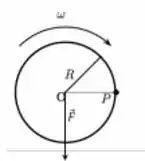
Questão 83
Uma bolinha, presa a uma das extremidades de um fio ideal tenso, gira em um plano vertical descrevendo uma circunferência. A velocidade da bolinha tem módulo constante. Quando o fio está na horizontal, a tração nele tem módulo igual a oito vezes o módulo do peso da bolinha. Podemos dizer que a razão entre as trações no fio nos pontos mais alto e mais baixo da trajetória circular da bolinha é
Questão 84
Um pequeno carro guiado por controle remoto possui massa de 1,60kg e é colocado numa pista circular vertical de abertura e de raio igual a . O carro parte do repouso da posição A e é submetido a uma aceleração tangencial constante de equanto se move na pista.
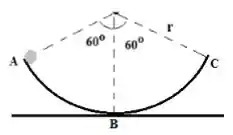
- Calcular o módulo da aceleração ao passar pela posição B, posição mais baixa da trajetória;
- Calcular a força normal que a pista faz sobre o carrinho na posição B;
- Calcular em C a velocidade do carro no momento em que perde contato com a pista;
- Qual é a força resultante agindo sobre o carro na posição B.
Questão 85
Uma corda é amarrada a uma pedra e esta é colocada em movimento circular com velocidade constante. Se a gravidade é ignorada e o período do movimento circular é duplicado, a tensão na corda é:
(a) Reduzida de do seu valor original.
(b) Reduzida de do seu valor original.
(c) Aumentada em vezes de seu valor original.
(d) Aumentada em vezes de seu valor original.
(e) Permanece em seu valor original.
Ver solução completaQuestão 86
Um brinquedo comum de criança consiste em duas pequenas esferas de madeira amarradas por um fio, de massa desprezível e comprimento , e que são postas para colidir acima e abaixo do ponto de sustentação. No instante retratado pelo desenho, cada bola tem uma velocidade linear e o fio está esticado. Considere que o eixo de rotação é fixo.
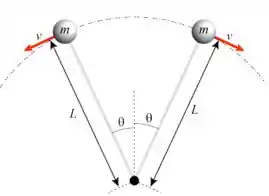
- Desenhe as forças atuando em cada esfera no instante mostrado no desenho.
- Calcule o módulo das acelerações centrípeta e tangencial em cada esfera.
- Qual é a tração no fio neste instante ?
- Calcule os torques da força peso e tração em cada uma das esferas, indicando direção e sentido, em relação ao eixo de rotação fixo.
- Calcule o momento angular de cada bola em relação ao eixo de rotação fixo, e o momento angular total do sistema.
Questão 87
Um corpo de massa movimenta-se dentro de um funil descrevendo uma trajetória circular de raio , com velocidade de módulo constante. A superfície laterial do funil, de atrito desprezível, faz um ângulo com a vertical como mostrado na figura. Sendo o módulo da força que a superfície faz sobre o corpo, sua velocidade será dada por
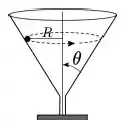
Questão 88
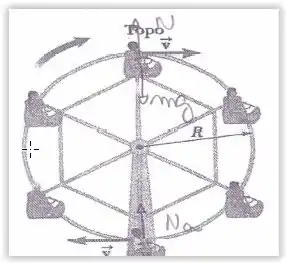
Uma criança de massa anda numa roda gigante como mostra a figura. A criança se move em um círculo vertical de raio com rapidez de
- Determine a força exercida pelo assent sobre a criança no ponto mais baixo da roda-gigante. Faça o diagram de corpo livre neste ponto.
- Determine a força exercida pelo assent sobre a criança no ponto mais alto da roda-gigante. Faça o diagram de corpo livre neste ponto.
- Suponha que um defeito no mecanismo da roda-gigante cause um aumento na velocidade da criança, que vai para . Qual é o peso da criança no topo da roda-gigante neste caso?
Questão 89
Uma moeda se encontra a uma distância do eixo de um disco que se encontra numa posição plana e tem raio . O coeficiente de atrito estático entre o disco e a moeda é . Suponha que a velocidade angular do disco aumenta de forma constante a partir do repouso. Qual será o módulo de sua velocidade angular no instante em que a moeda iniciará a escorregar?
Questão 92
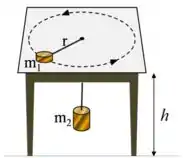
Questão 3). Um disco de metal de massa descreve uma circunferência horizontal de raio sobre uma mesa sem atrito, de altura , enquanto permanece ligado a um cilindro de massa pendurado por uma corda inextensível, de massa desprezível, que passa por um furo no centro da mesa, conforme representa a figura ao lado (sem escala). O disco () se move com velocidade constante, em módulo, para manter o cilindro () em repouso. A corda se rompe e o disco de massa é lançado horizontalmente, chegando ao solo depois de percorrer uma distância horizontal . Sabendo que e que o alcance é o dobro da altura da mesa , determine o raio da circunferência descrita pelo disco antes da corda se romper. Escreva sua resposta em termos de . 🤔
Questão 93
Estradas e rampas de saída circulares em rodovias são frequentemente elevadas, para permitir que um veículo circule nelas com velocidade de até . Para projetar uma rampa semelhante que suporte uma velocidade de (desprezando o atrito), deve-se:
(a) aumentar o raio por um fator de .
(b) aumentar o raio por um fator de .
(c) diminuir o raio por um fator de .
(d) diminuir o raio por um fator de .
(e) aumentar o raio por um fator de .
Ver solução completaQuestão 94
Marque a alternativa incorreta:
A. O trabalho da força centrípeta é sempre zero.
B. A força de atrito nunca pode ser uma força centrípeta.
C. Quando o movimento circular não é uniforme, a aceleração só tem componente centrípeta.
D. A velocidade num movimento circular, uniforme ou não, é um vetor ortogonal ao vetor distância ao centro da trajetória.
E. A aceleração angular instantâne é sempre igual à derivada da velocidade angular pelo tempo.
Ver solução completaQuestão 95
Um carro pequeno de massa viaja em uma pista horizontal. Como ilustrado pela figura abaixo, em certa posição a pista possui um loop, uma circunferência vertical de raio :

Qual é a aceleração mínima, para que o carro, no topo do loop não perca o contato das suas rodas com a pista?
a) , com o sentido do vetor aceleração para baixo.
b) , com o sentido do vetor aceleração para cima.
c) , com o sentido do vetor aceleração para cima.
d) , com o sentido do vetor aceleração para baixo.
e) , com o sentido do vetor aceleração para cima.
Ver solução completaQuestão 99
Um carro parte do repouso numa pista curcular com raio de . O motorista mantém o carro com aceleração constante igual a na direção da velocidade. Que ângulo, em graus, terá descrito o carro quando o módulo de sua aceleração for ?
Ver solução completaQuestão 100
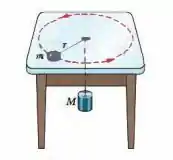
(Cap 6 – Ex 55) Um disco de metal de massa descreve uma circunferência de raio sobre uma mesa sem atrito enquanto permanece ligado a um cilindro de massa pendurado por um fio que passa por um furo no centro da mesa (Fig. 6-43). Que velocidade do disco mantém o cilindro em repouso?
Questão 101
(Cap 6 – Ex 49) Um estudante que pesa está sentado, com as costas eretas, em uma roda-gigante em movimento. No ponto mais alto, o módulo da força normal exercida pelo assento sobre o estudante é . (a) O estudante se sente mais leve ou mais pesado neste ponto? (b) Qual é o módulo de no ponto mais baixo? Se a velocidade da roda-gigante é duplicada, qual é o módulo da força normal (c) no ponto mais alto e (d) no ponto mais baixo?
Ver solução completaQuestão 102
(Cap 6 – Ex 51) Um bonde antigo dobra urna esquina fazendo uma curva plana com de raio a . Qual é o ângulo que as alças de mão penduradas no teto fazem com a vertical?
Ver solução completaQuestão 103
Um planeta de massa possui dois satélites de massas iguais a percorrendo a mesma órbita circular de raio . Sabe-se que os satélites estão sempre em posições diametralmente opostas. Nos itens abaixo dê suas respostas em termos de e da constante universal da gravitação .
Determine o módulo da força gravitacional que atua em cada satélite.
Calcule o período de revolução do sistema.
Ver solução completaQuestão 104
Um carro faz uma curva plana horizontal com velocidade de módulo constante v. Considere as afirmativas:
I A força de atrito é a força de reação à força centrípeta.
II. A aceleração do carro na curva é nula em módulo.
III. Quanto maior o raio da curva maior deve ser o módulo da força de atrito sobre o carro para que ele descreva essa curva com velocidade de módulo v.
Quais afirmativas são verdadeiras:
a) Nenhuma.
b) Apenas I
c) Apenas II
d) Apenas III
e) Apenas I e II
f) Apenas I e III
g) Apenas II e III
h) Todas
Ver solução completaQuestão 105
Um objeto de massa se move em uma trajetória curvilínea, como na figura abaixo. Qual dos diagramas abaixo representa a combinação correta da força atuando no objeto, sua velocidade e sua aceleração , no ponto considerado?
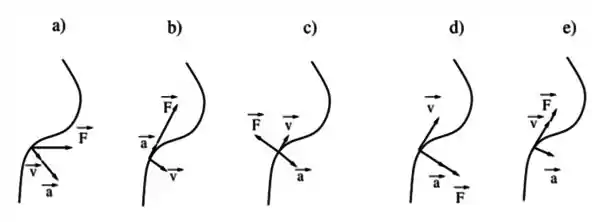
Questão 106
Um trem atravessa uma curva de raio de curvatura igual a 100m a 30km/h. A distância entre os trilhos é de 1m. De que altura é preciso levantar o trilho externo para minimizar a pressão que o trem exerce sobre ele ao passar pela curva ?
Ver solução completaQuestão 107
15 - Um carro passa com velocidade constante por uma colina circular e por um vale circular de mesmo raio. No alto da colina, a força normal exercida sobre o motorista pelo assento do carro é zero. A massa do motorista é de . Qual é o modulo da força normal exercida pelo assento sobre o motorista quando o carro passa pelo fundo do vale?
A)
B)
C)
D)
E)

Questão 108
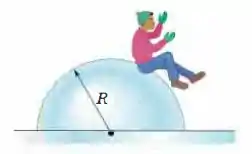
Um garoto está inicialmente sentado no alto de um monte hemisférico de gelo de raio . Ele começa a deslizar para baixo com uma velocidade inicial tão pequena que pode ser desprezada (ver figura). Suponha que o atrito seja desprezível. Em que altura o menino perde contato com o gelo?
Questão 109
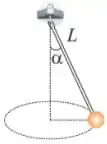
Q - Uma partícula de massa está suspensa por uma corda de massa desprezível e comprimento . A extremidade superior da corda pode girar mantendo um ângulo com a vertical, como mostrado na figura. A partícula descreve um movimento circular. Determine o módulo do vetor velocidade da partícula (expresse o resultado em ). Despreze qualquer atrito e/ou arraste.
Questão 110
Uma partícula se move sobre uma calha horizontal lisa com velocidade constante de módulo desconhecida. A calha horizontal transforma-se, suavemente, a partir do ponto A, em uma calha semicircular de raio R, tal como indicado na figura. Após percorrer toda a calha semicircular, a partícula deixa a calha no ponto B, que se encontra exatamente acima do ponto A, com velocidade horizontal de módulo v0 e cai de volta na calha horizontal em um ponto P. As calhas estão orientadas de modo que todo o movimento da partícula se passa num mesmo plano vertical. Considere desprezível o atrito entre a partícula e as calha em todos os momentos (entre os pontos A e B). Considere como dados do problema , e a aceleração da gravidade .
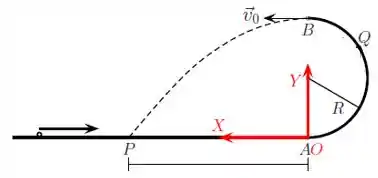
d) Determine o módulo da força que a calha semicircular exerce sobre a partícula quando essa passa pelo ponto B.
e) A partícula possui velocidade de módulo igual, maior ou menor que ao passar pelo ponto Q? Justifique claramente sua resposta.
Ver solução completaQuestão 112
(Cap 6 – Ex 44) Suponha que o coeficiente de atrito estático entre a estrada e os pneus de um carro é e não há sustentação negativa. Que velocidade deixa o carro na iminência de derrapar quando faz uma curva não compensada com de raio?
Ver solução completaQuestão 113
Num parque de diversões, um carrinho desce de uma altura , a partir do repouso, para dar a volta no loop de raio indicado na figura .
a) Desprezando o atrito do carrinho com o trilho, qual é o menor valor de necessário para permitir ao carrinho dar a volta completa?
Ver solução completaQuestão 114
Num parque de diversões, um carrinho desce de uma altura , a partir do repouso, para dar a volta no loop de raio indicado na figura .
c) Que acontece com o carrinho para ?
Ver solução completaQuestão 115
Num parque de diversões, um carrinho desce de uma altura , a partir do repouso, para dar a volta no loop de raio indicado na figura .
b) Se o carrinho cai no trilho em um ponto rotulado por , quando ainda falta percorrer mais um ângulo para chegar até o topo . Calcule .
Ver solução completaQuestão 116
O pêndulo da figura abaixo é formado por uma haste rígida de massa desprezível, com uma bola de massa em sua extremidade. A bola na extremidade do pêndulo descreve um arco de círculo de raio que atinge a sua altura máxima no ponto B.
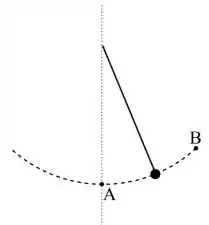
Sobre as forças que agem sobre a bola, escolha a alternativa correta:
(A) No ponto A, a tração da haste é igual à força da gravidade sobre a bola.
(B) No ponto A, a tração da haste é maior do que a força da gravidade sobre a bola.
(C) No ponto B, a tração da haste é nula.
(D) No ponto A, a força resultante sobre o pêndulo é nula.
(E) As forças que atuam sobre a bola são a gravidade, a tração da haste e a força centrípeta
Ver solução completaQuestão 117
Uma massa se encontra presa à extremidade de um fio. A outra extremidade do fio está presa num ponto no interior de um carro que se move com velocidade constante numa pista circular. Quais são as forças que atuam diretamente na massa?
(A)Tensão e gravidade.
(B) Tensão.
(C) Tensão, gravidade e força centrípeta.
(D)Tensão, gravidade, força centrípeta e atrito.
(E) Tensão, gravidade e força centrífuga.
Ver solução completaQuestão 118
Uma caixa encontra-se sobre um carrossel, a uma distância do eixo de rotação. Inicialmente todo o sistema encontra-se em repouso. No instante o motor do carrossel é ligado e sua velocidade angular aumenta linearmente com o tempo, até atingir um valor máximo no instante , conforme mostrado na figura. Depois disso, a velocidade angular permanece constante neste valor máximo. Suponha que a caixa não escorregue em nenhum momento.
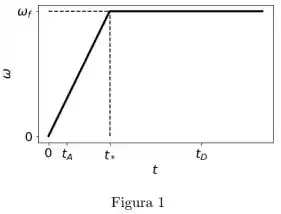
Suponha, agora, que em a caixa esteja na iminência de escorregar. Se , e , qual é o valor do coeficiente de atrito estático entre a caixa e o carrossel?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 119
(Cap 6 – Ex 43) Um gato está cochilando em um carrossel parado, a uma distância de do centro. O brinquedo é ligado e logo atinge a velocidade normal de funcionamento, na qual completa uma volta a cada . Qual deve ser, no mínimo, o coeficiente de atrito estático entre o gato e o carrossel para que o gato permaneça no mesmo lugar, sem escorregar?
Ver solução completaQuestão 120
(Cap 6 – Ex 59) Na Fig. 6-45, uma bola de é ligada por meio de dois fios de massa desprezível, cada um com comprimento , a uma haste vertical giratória. Os fios estão amarrados à haste a uma distância um do outro e estão esticados. A tensão do fio de cima é . Determine (a) a tensão do fio de baixo; (b) o módulo da força resultante a que está sujeita a bola; (c) a velocidade escalar da bola; (d) a direção de
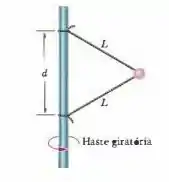
Questão 121
Em algum ponto da trajetória de determinada partícula, os vetores velocidade e aceleração são dados pelo diagrama abaixo.
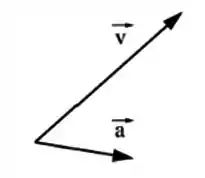
Dada a trajetória abaixo, determine que ponto da trajetória é compatível com este diagrama.
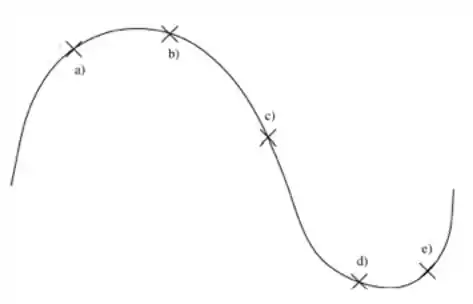
Questão 122
(Cap 6 – Ex 53) Um avião está voando em uma circunferência horizontal com uma velocidade de (Fig. 6-41). Se as asas estão inclinadas de um ângulo com a horizontal, qual é o raio da circunferência? Suponha que a força necessária para manter o avião nessa trajetória resulte inteiramente de uma "sustentação aerodinâmica" perpendicular à superfície das asas.
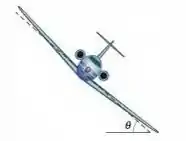
Questão 123
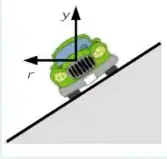
. Um automóvel descreve uma curva com inclinação como indicado na figura. O coeficiente de atrito estático é e o raio da trajetória circular é . Nestas condições o automóvel pode se manter na curva sempre que sua velocidade escalar esteja dentro de certos valores máximos e mínimos. Determine a velocidade mínima com a qual o carro pode fazer a curva sem deslizar.
Questão 124
. Um avião aeromodelo (massa ) voa em um círculo horizontal de raio com velocidade escalar constante , preso a um fio ideal que exerce a força de tração , fazendo um ângulo de com a horizontal que passa pelo centro do avião. A força de sustentação aerodinâmica faz um ângulo de com a vertical que passa no centro do avião. A figura abaixo mostra as forças que atuam sobre o avião. Determine e a tração do fio .

Questão 125
Parte II:
A inclinação de em uma curva com raio na pista de corrida de carros permite que atinjam a velocidade máxima de sem derrapar para fora da pista. Admita o valor de para a massa de um desses carros. Suponha o carro como uma partícula.

(c) Determine o coeficiente de atrito estático dos pneus com a pista.
Ver solução completaQuestão 126
Uma extremidade de um fio de de comprimento é fixa, e a outra é ligada a uma pedra de . A pedra descreve uma circunferência vertical, passando pelo ponto mais alto com uma velocidade de . A tração no fio (em newtons) nesse ponto é aproximadamente:
Dado:
A.
B.
C.
D.
E.
Ver solução completaQuestão 127
Em um dia gelado de inverno, o coeficiente de atrito entre os pneus de um carro e a estrada é reduzido a um quarto do seu valor em dia seco. Como resultado, a rapidez máxim na qual o carro pode percorrer com segurança a mesma curva de raio é igual a
reduzida de uma quantidade desconhecida que depende da massa do carro.
Ver solução completaQuestão 128
2) Um pêndulo cônico é formado por uma partícula de massa , suspensa por um fio ideal, que faz um ângulo com a vertical e realiza um movimento circular, como mostra a figura. Considere o módulo da aceleração da gravidade.
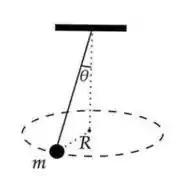
Sabendo que a velocidade angular de rotação é , o raio do movimento circular descrito pela massa é:
a)
b)
c)
d)
e)
Ver solução completaQuestão 129
Quando um carro está fazendo uma curva com velocidade constante, é correto afirmar que:
(A) Tem uma força centrípeta atuando sobre o carro, mas não podemos saber qual a sua origem
(B) O peso efetivo do carro diminui, para que ele consiga fazer a curva
(C) A força centrípeta é uma força de atrito exercida pela estrada sobre os pneus
(D) Não há força centrípeta atuando no carro
(E) A força centrípeta é a força peso, e por isto o carro consegue fazer a curva
Ver solução completaQuestão 130
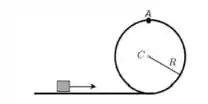
7) Uma partícula de massa m realiza um loop de raio . No ponto mais alto do loop, o módulo da força normal é . Determine o módulo da velocidade da partícula neste ponto.
Questão 131
A força centrípeta é melhor explicada por qual das seguintes afirmações?
(A) A força centrípeta é uma força fundamental da natureza
(B) A força centrípeta é uma força dirigida radialmente para fora a partir do centro da sua órbita
(C) A força centrípeta é a força resultante sobre um objeto em órbita que o mantém em movimento circular
(D) A força centrípeta é a força dirigida ao longo de uma linha que é tangente à órbita
(E) A força centrípeta é a mesma coisa que a força centrífuga; são sinônimos.
Ver solução completaQuestão 132
Um menino está inicialmente em repouso sentado no alto de um monte hemisférico de gelo de raio . Ele começa a deslizar com uma velocidade inicial tão pequena que pode ser desprezada. Suponha que o atrito com o gelo seja desprezível. Em que altura o menino perde contato com o gelo.
Ver solução completaQuestão 133
Um carro percorre a 18 m/s uma curva não inclinada de raio igual a 1,0 x . Qual deve ser o valor do coeficiente de atrito estático mínimo entre o pavimento e os pneus para que o carro não derrape?
(A) 0,33
(B) 0,66
(C) 0,99
(D) 0,55
(E) 0,88
Ver solução completaQuestão 134
Um trecho de um trilho de montanha-russa, quando o carrinho está andando com velocidade de módulo constante, é representado pela figura abaixo. Em quais dos pontos representados o carrinho tem aceleração aproximadamente nula?
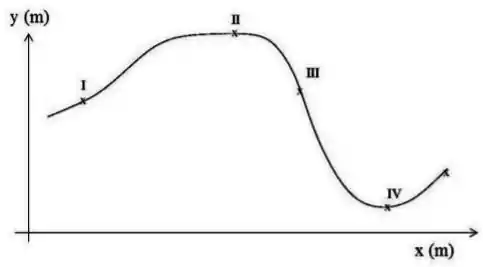
a) pontos e
b) pontos e
c) ponto
d) ponto
e) nenhum
Ver solução completaQuestão 135
Uma partícula descreve uma trajetória de modo que em um certo ponto os vetores velocidade e aceleração são dados pelo diagrama abaixo.
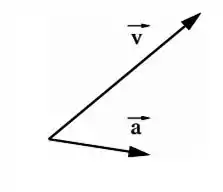
Dada a trajetória abaixo, que ponto da trajetória é compatível com este diagrama?
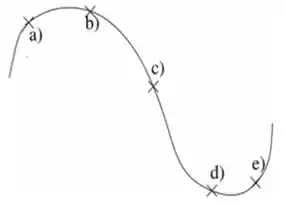
Questão 137
Um carro pequeno parte do repouso no ponto e segue uma trajetória circular, no sentido anti-horário, como indicado na figura. O módulo de sua velocidade aumenta a uma taxa constante. A alternativa que melhor representa o vetor aceleração nas diferentes posições da primeira volta é:
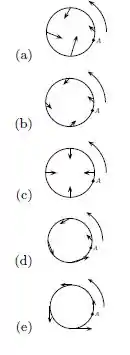
Questão 139
Uma bola de massa está amarrada numa corda e gira descrevendo um círculo vertical com velocidade cujo módulo é constante e vale , como mostrado no diagrama abaixo. Em que ponto a corda tem maior probabilidade de quebrar, porque tem a maior tensão?
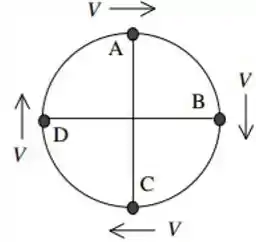
a) posição .
b) posição .
c) posição .
d) posição .
e) Nenhuma das alternativas anteriores.
Ver solução completaQuestão 140
Em , um bloco de massa está inicialmente em repouso sobre um plano horizontal e conectado a uma barra rígida de massa desprezível e comprimento que pode girar em torno do ponto O. Um torque é então aplicado à barra, tal que possui uma aceleração angular constante. Existe atrito entre e a superfície horizontal, tal que os coeficientes de atrito estático e cinético são, respectivamente e . Considere .
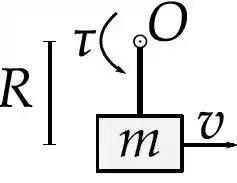
(c) Suponha agora que a barra rígida suporte uma tração máxima de . Qual é a maior velocidade da massa para que a barra não se rompa?
Ver solução completaQuestão 141
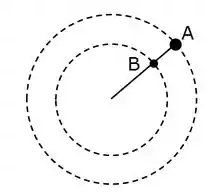
Na figura, as duas partículas, e , ligadas por um fio inextensível e de massa desprezível, descrevem trajetórias circulares concêntricas sobre uma superfície horizontal sem atrito. A partícula está presa por fio, também inextensível e de massa desprezível a um eixo fixo na mesa. Ambas as partículas completam simultaneamente, uma volta a cada segundo e os raios de suas órbitas são e . As massas das partículas são e . Sabendo-se que a tensão no fio entre as partículas e é igual a , qual é a tensão no fio que liga a partícula ao eixo?
A)
B)
C)
D)
E)
Questão 142
A figura mostra um motociclista que precorre um Globo da Morte de raio sem deixar de estar em contato com o mesmo. No ponto (A) que faz um ângulo com a vertical, sua velocidade é e se mantém constante. A massa da moto e motociclista é .
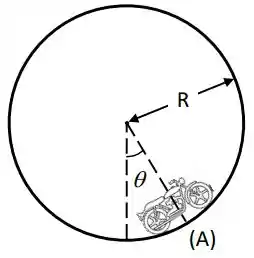
(a) Faça o diagrama de corpo isolado da motocicleta no ponto (A).
(b) Suponha que e e calcule o módulo da força normal no ponto (A), .
(c) Suponha que no ponto (A) a força de atrito estática com o solo atinge seu valor máximo. Use o resultado do item anterior para calcular o coeficiente de atrito estático .
Ver solução completaQuestão 143
. Uma criança está brincando com um barbante de com uma massa de presa em
sua extremidade. Segurando na outra extremidade do barbante, a criança começa a girar a
massa em um movimento de rotação na horizontal e acelerar o movimento de rotação até o
momento em que a velocidade na qual a massa está se movendo é de . Neste instante,
o barbante se rompe. A tração máxima suportada pelo barbante é de:
Ver solução completaQuestão 144
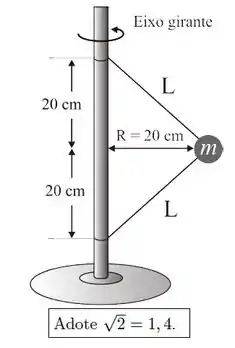
Uma partícula de massa está presa a uma haste vertical por duas cordas inextensíveis de massas desprezíveis. Quando colocada em movimento, a massa descreve um círculo horizontal de raio , com as cordas esticadas. A máxima tensão que cada fio pode suportar sem arrebentar é . Quando o sistema é colocado para girar em torno da haste com velocidade s podemos afirmar que:
Questão 145
Um carro fica sem gasolina e desce uma colina em ponto-morto. Ele prossegue assim atravessando o vale e começa a subida pelo outro lado. No momento em que o carro passa exatamente pelo fundo do vale, qual dos diagramas de corpo livre da figura abaixo está correto?
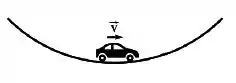
O carro se move para a direita, e a força de arraste e a de atrito de rolamento são desprezíveis.
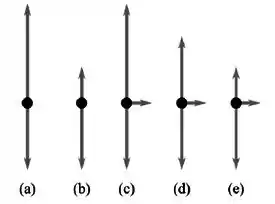
Questão 146
Quatro partículas idênticas descrevem movimentos circulares concêntricos, em um plano horizontal, e estão conectadas entre si através de fios ideais do mesmo tipo, conforme a figura. Aumenta-se a frequência angular da rotação gradativamente. Nestas condições, o fio que se arrebenta primeiro é o de número
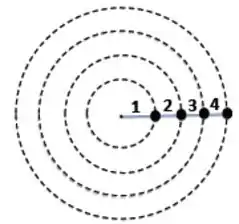
(a) 1
(b) 2
(c) 3
(d) 4
(e) 1, 2, 3 e o 4 simultaneamente
Ver solução completaQuestão 147
Suponha que o coeficiente de atrito estático entre os pneus de um carro de massa m e a estrada onde ele trafega é
3) caso a pista seja inclinada na curva (curva compensada) e faça um ângulo com a horizontal, qual seria a maior velocidade escalar com que o carro completaria uma curva de raio R (ainda com atrito) sem deslizar?
Ver solução completaQuestão 148
Parte I:
Um corpo de massa suspenso por um fio de comprimento , que faz um ângulo com a vertical, gira descrevendo uma circunferência de raio . Esse dispositivo é designado pela expressão pêndulo cônico.
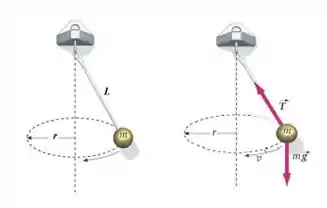
(a) Obtenha uma expressão literal para o período desse pêndulo em função de , e . A expressão pode conter , desde que seja indicada outra fórmula para calculá-lo em termos das grandezas pedidas.
(b) Considere , e . Calcule o período desse pêndulo.
Ver solução completaQuestão 149
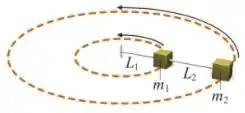
Q - Um bloco de massa está preso a um fio, de comprimento , que está fixo na outra extremidade. O bloco desloca-se num círculo horizontal, suportado por uma mesa sem atrito. Um segundo bloco, de massa , está ligado ao primeiro por um fio de comprimento e também se desloca num círculo, conforme mostrado na figura. Se os dois blocos giram com velocidade angular , a tensão no fio de comprimento , em Newtons, é:
Questão 150
Um automóvel descreve uma curva compensada que faz um ângulo com a horizontal. A massa do carro é e o raio da curva é dado por . Utilize o número apropriado de algarismos significativos.
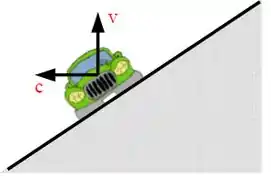
Dados:
a) Determine a velocidade necessária para que o carro faça a curva com segurança sem precisar do auxílio do atrito.
b) Indique no desenho todas as forças que agem no carro quando sua velocidade for igual a . Escreva as equações para o movimento do carro nesta situação usando o sistema de eixos indicado no desenho. O sistema de equações não precisa ser resolvido.
Ver solução completaQuestão 151
Sobre o tampo de uma mesa horizontal sem atrito, dois blocos (massas m e M, onde M>m) executam um movimento circular com velocidade escalar constante ) ao redor do ponto O, onde uma corda de comprimento L, esticada na horizontal, prende o bloco M. Como há atrito entre os blocos, seus centros se mantêm alinhados e o bloco m não desliza sobre o bloco M. Use g como aceleração da gravidade.

- Faça o diagrama de forças sobre cada bloco
- Determine o módulo de todas as forças normais sobre cada bloco em função de m, M e g.
- Encontre uma expressão para o coeficiente de atrito μ entre os blocos em termos de v, L e g. Qual é o tipo de atrito envolvido: estático ou cinético? Justifique.
- Determine uma expressão para o módulo da tensão T na corda em termos de m, M, v e L. O valor de T é maior, menor ou igual ao módulo da força de atrito fat entre os blocos? Justifique.
Questão 152
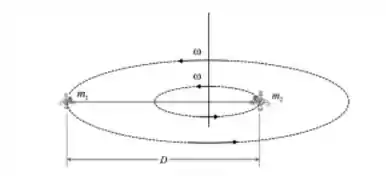
Após um acidente, dois astronautas se encontram isolados no espaço, ligados por um cabo esticado de comprimento , e, girando com velocidade angular em relação a um eixo ortogonal ao cabo e que passa pelo centro de massa do sistema formado por eles (ver figura). Podemos considerar que as dimensões dos astronautas são muito menores que a extensão do cabo e, trata-los como se fossem duas partículas. Sabendo que os dois astronautas têm massas relacionadas por , calcule o raio da trajetória circular do astronauta de massa
a)
b)
c)
d)
e)
Ver solução completaQuestão 153
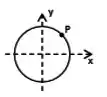
O ponto P na figura indica a posição de um objeto que move-se ao longo da circunferência com rapidez constate no sentido horário. Qual das setas melhor representa a direção da aceleração do objeto no ponto P?
![]()
![]()
![]()
![]()
![]()
Questão 156
Os pneus de um carro de massa têm coeficiente de atrito estático com a pista horizontal de uma rodovia em uma curva circular de raio . A velocidade máxima com que o corpo pode fazer essa curva sem derrapar é . Supondo que o carro faça a curva com velocidade de módulo constante , podemos dizer que, nesse caso, a força de atrito estático entre os pneus e a pista tem módulo igual a
Questão 157
Uma partícula de massa pendurada por um fio idel de comprimento é abandonada de um ângulo a partir do repouso com o fio totalmente estendido, como mostra a figura abaixo. Sejam a tração no fio e o peso as forças que atuam na partícula e despreze a resistência do ar. Qual das afirmações está correta?
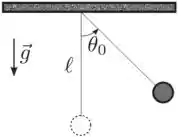
- varia com o ângulo
- O módulo da aceleração da partícula é constante
- No ponto mais baixo da trajetória, onde é o módulo da velocidade neste ponto
- Para , a aceleração é nula
- No ponto mais baixo da trajetória
Questão 158
Um carro de massa descreve sem derrapar uma curva no plano horizontal de raio com velocidade . O gráfico ao lado indica o comportamento da força de atrito para este caso específico.
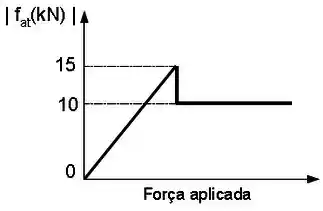
(b) Determine a velocidade máxima com que o carro pode fazer a curva sem derrapar.
Ver solução completaQuestão 159
Suponha que o coeficiente de atrito estático entre os pneus de um carro de massa e a estrada onde ele trafega é
2) uma pessoa alega que, se o peso do carro fosse aumentado, essa velocidade escalar limite (com a qual o carro completa a corva sem deslizar) seria maior, uma vez que a força de atrito seria maior. Essa afirmação está correta? Explique
Ver solução completa