Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 63
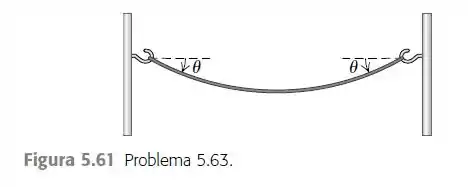
Em quase todos os problemas deste livro, as massas dos cabos, cordas e fios são tão pequenas em comparação com os outros corpos que podemos desprezá-las. Porém, quando a corda é o único objeto do problema, obviamente a sua massa não pode ser desprezada. Por exemplo, suponha que você amarre as extremidades de uma corda em dois suportes verticais para secar roupas (Figura 5.61). A corda possui massa M e cada extremidade faz um ângulo com a horizontal. Determine a) a tensão nas extremidades da corda; b) a tensão em seu ponto inferior. c) Por que não pode ser igual a zero? (Veja o item Q5.3 das Questões para Discussão.) d) Discuta seus resultados para os itens a) e (b) no limite em que . A corda
para secar roupa ou qualquer cabo flexível preso em suas extremidades sob ação do próprio peso adquire a forma de uma catenária. Para um tratamento mais avançado dessa curva, veja
SYMON, K. R. Mechanics, 3. ed. Addison-Wesley, Reading, MA, 1971. p. 237-241..
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá a seguinte figura que mostra uma corda de massa com extremidades presas em dois suportes verticais da seguinte forma:
Os ganchos exercem forças nas extremidades da corda. Em cada gancho, a força que o gancho exerce e a força devido à tensão na corda é um par de ação-reação.
Queremos calcular a tensão nas extremidades da corda e no centro. Também devemos dizer o porquê que não pode ser .
Depois, devemos calcular as mesmas tensões... mas fazendo o limite para .
Para resolver isso, temos que fazer um diagrama de corpo livre da corda e analisar as forças que estão atuando nela.
Também, utilizaremos também a segunda Lei de Newton:
Onde é a força resultante, é a massa e é a aceleração.
Passo 2
- As forças verticais que os ganchos exercem devem equilibrar o peso da corda, de modo que cada gancho exerce uma força vertical para cima de na corda.
- Cada metade da corda está em equilíbrio, então a tensão no meio deve equilibrar a força horizontal que cada gancho exerce, que é o mesmo que o componente horizontal da força devido à tensão no final:
- Matematicamente falando, porque isso causaria uma divisão por zero na equação para o ou
Portanto, a força descendente que a corda exerce em cada extremidade é:
Onde é a aceleração da gravidade.
Passo 3
Passo 4
Fisicamente falando, precisaríamos de uma tensão infinita para manter uma corda sem massa perfeitamente reta.
Assim, a tensão na corda não é a mesma em todos os pontos ao longo da corda.