Exercícios de Tração em Cabos - Lista de Exercícios Resolvida
Questão 1
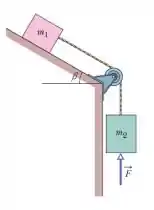
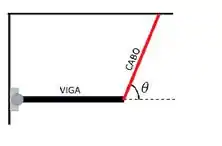
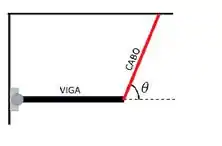
A figura ao lado ilustra uma viga homogênea de peso P. A viga está sustentada na posição horizontal por uma dobradiça e por um cabo, que forma um ângulo em relação à direção da viga, como ilustrado ao lado. Quais são o módulo e o sentido da força horizontal que a dobradiça exerce sobre a viga?
a)
b)
c)
d)
e)
f)
g)
h)
i) 0
Ver solução completaQuestão 2
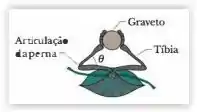
Alguns insetos podem se deslocar pendurados em gravetos. Suponha que um desses insetos tenha massa m e esteja pendurado em um graveto horizontal, como mostra a figura abaixo, com um ângulo . As seis pernas do inseto estão sob a mesma tensão e asseções das pernas mais próximas do corpo são horizontais.
a) Qual é a razão entre a tensão em cada tíbia (extremidade da perna) e o peso do inseto?
b) Se o inseto estica um pouco as pernas, a tensão nas tíbias aumenta, diminui ou continua a mesma?
Questão 3
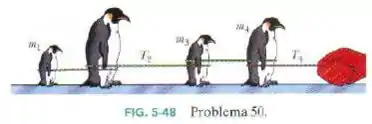
A Fig. 5-48 mostra quatro pinguins que estão sendo puxados sobre o gelo muito escorregadio (sem atrito) por um zelador. As massas de três pinguins e a tensão em duas das cordas são e . Determine a massa do pinguim , que não é dada.
Questão 4
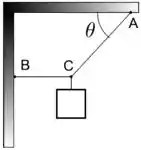
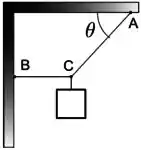
Dois fios ideais e estão presos a um teto horizontal e a uma parede vertical nos respectivos pontos e , como indica a figura. Na extremidade comum dos fios está suspenso e em equilíbrio um bloco de peso . O fio é perpendicular à parede e o fio faz um ângulo com o teto . O módulo da tensão no fio é igual a
Questão 5
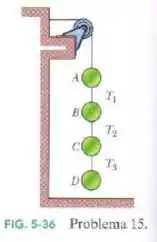
A Fig. 5-36 mostra um arranjo no qual quatro discos estão suspensos por cordas. A corda mais comprida, no alto, passa por uma polia sem atrito e exerce uma força de sobre a parede à qual está presa. As tensões nas cordas mais curtas são , e . Quais são as massas (a) do disco A, (b) do disco B, (c) do disco C e (d) do disco D?
Questão 6
Três macacos , e , de mesmo peso, estão pendurados em repouso, cada um em um cipó, com os cipós amarrados em um galho de árvore. A partir de um dado instante o macaco sobe em seu cipó com velocidade constante, o macaco sobre no seu com aceleração para cima constante e o macaco desce no seu com aceleração para baixo constante. Supondo que os cipós sejam fios ideiais (inextensíveis com massa desprezível), que os movimentos se processem na vertical, que as acelerações mencionadas não sejam nulas, e denotando por , e as tensões nos cipós dos respectivos macacos , e , podemos dizer que
Questão 7
Dois fios ideais e estao presos a um teto horizontal e a uma parede vertical nos respectivos pontos e , como indica a figura. Na extremidade comum dos fios está suspenso e em equilíbrio um bloco de peso . O fio é perpendicular à parede e o fico faz um ângulo com o teto . O módulo da tensão no fio é igual a
Questão 8
Dois blocos de massas e estão em movimento retilíneo sobre uma superfície horizontal sem atrito e ligados por um fio ideal horizontal que se mantém tenso durante o movimento.Sobre os blocos agem forças constante na direção do movimento, como mostra a figura. O módulo da tensão do fio é

- ;
- ;
- ;
- ;
- ;
Questão 9
Um lustre é pendurado em um teto horizontal por dois fios, considerados ideais, que se juntam e são ligados ao lustre, como mostra a figura. Em um dos fios, que faz um ângulo de com o teto, a tensão tem módulo ; no outro, que faz um ângulo com o teto, a tensão tem módulo . Considerando o sistema de eixos com na vertical, como indicado na figura, obtemos que a razão entre as componentes verticais e das tensões é
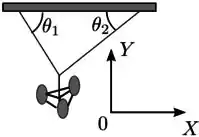
- ;
- ;
- ;
- ;
- ;
Questão 10
Na figura ao lado, uma barra não homogênea de comprimento L está suspensa em repouso, na horizontal, por duas cordas de massa desprezível. A corda 1 faz um ângulo com a vertical e a corda 2 faz um ângulo com a vertical.
(a) (1,5) Qual a razão T1/T2 entre as tensões na corda 1 e corda 2 respectivamente?
(b) (2,0) Em função de L, qual a distância x entre a extremidade esquerda da barra e o centro de massa?
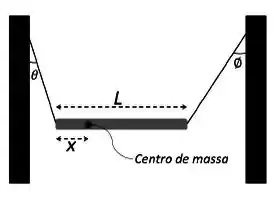
Questão 11
Uma pequena esfera de massa é suspensa por um fio com massa desprezível. O sistema está preso no teto de um carro, como mostra a figura abaixo. Quando o carro está em repouso, a corda está na posição vertical; quando o carro se move com aceleração constante, a corda faz um ângulo com a vertical.

a) Faça um desenho da esfera com a corda, e indique as forças que atuam na esfera quando o carro tem aceleração constante para frente.
b) Se a corda faz um ângulo com a vertical, qual é a aceleração (módulo, direção e sentido) do carro? Se necessário, use e .
c) Se o carro se move com velocidade constante a , qual é o ângulo que a corda faz com a vertical? Neste caso, qual é o módulo da tração na corda?
Ver solução completaQuestão 12
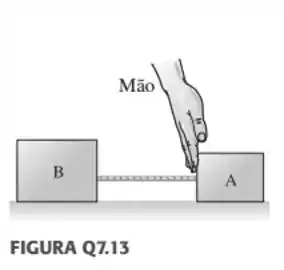
Os dois blocos na figura abaixo estão conectados por uma corda pesada e uniforme com massa de . Uma força de é aplicada para cima, como mostrado.
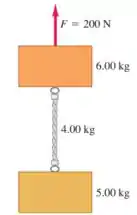
(a) Desenhe três diagramas de corpo livre: um para o bloco de , um para a corda de , e outro para o bloco de . Para cada força, indique qual corpo é seu gerador.
Ver solução completaQuestão 13
Três cordas horizontais puxam uma grande pedra presa ao chão, produzindo as forças vetoriais: mostradas na figura abaixo. Encontre a magnitude e a direção de uma quarta força na pedra que fará com que fará com que a soma vetorial das quatro forças seja zero.
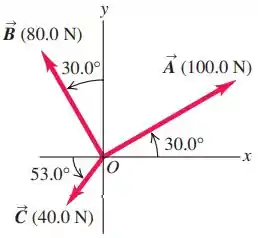
Questão 14
Os dois blocos na figura abaixo estão conectados por uma corda pesada e uniforme com massa de . Uma força de é aplicada para cima, como mostrado.
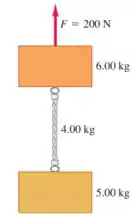
(b) Qual é a aceleração do sistema?
Ver solução completaQuestão 15
Os dois blocos na figura abaixo estão conectados por uma corda pesada e uniforme com massa de . Uma força de é aplicada para cima, como mostrado.
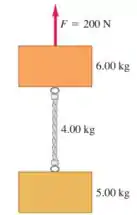
(c) Qual a tensão no topo da corda pesada?
Ver solução completaQuestão 16
Um fio metálico de massa desprezível está preso a uma parede no ponto e sustenta uma caixa de massa fixa em sua outra extremidade no ponto . O segmento do fio faz um ângulo de 60° com a parede. No ponto , o fio se apoia em uma roldana fixa. A força de sustentação que a roldana exerce sobre o fio está representada na figura ao lado por seu módulo e inclinada de um ângulo em relação à horizontal.
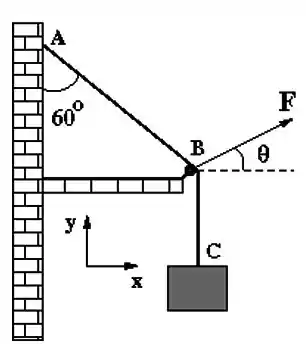
a) Determine o valor do ângulo e o módulo da força .
b) Com exceção das forças-peso, explicite nos corpos correspondentes (parede, roldana, fio e bloco) os pares ação-reação de todas as forças relevantes neste problema.
Ver solução completaQuestão 17
Um bonde antigo, trafegando a , faz uma curva (plana) à direita com de raio. Neste bonde, existem alças de mão fixas ao teto, com liberdade para inclinar-se em qualquer direção.
c) Vistas por algum passageiro no fundo do bonde, em que direção as alças de mão se inclinam quando o bonde faz a curva? Justifique.
d) Qual é o ângulo que as alças de mão fazem com a vertical?
Ver solução completaQuestão 18
Dois blocos homogêneos de massa e massa , estão ligados por uma corda grossa inextensível de massa . Uma força atua para cima no bloco de massa conforme ilustrado na figura. Utilize .
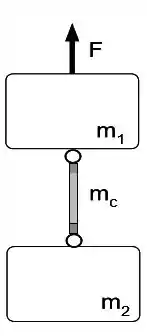
a) Calcule o módulo da tensão na corda desprezando sua massa.
b) Agora leve em consideração a massa da corda. Note que neste caso a tensão não será a mesma ao longo de toda a extensão da corda. Faça um diagrama de corpo livre para os blocos e a corda. Escreva as equações de movimento para o sistema na sua forma literal.
c) Calcule os módulos das tensões na extremidade superior e na extremidade inferior da corda.
Ver solução completaQuestão 20
(Capítulo 5.9 – Exercício 18) Tarzan, que pesa , salta de um rochedo na ponta de um cipó de que está preso ao galho de uma árvore e faz inicialmente um ângulo de com a vertical. Suponha que um eixo é traçado horizontalmente a partir da borda do rochedo e que um eixo é traçado verticalmente para cima. Imediatamente após Tarzan pular da encosta, a tensão do cipó é . Nesse instante, quais são (a) a força do cipó sobre Tarzan em termos dos vetores unitários, a força resultante sobre Tarzan (b) em termos dos vetores unitários e como (c) módulo e (d) ângulo em relação ao sentido positivo do eixo . Quais são (e) o módulo e (f) o ângulo da aceleração de Tarzan nesse instante?
Ver solução completaQuestão 21
Considere a figura abaixo que mostra dois blocos de massas m1 = 11,5
kg e m2 = 4,9 kg ligados por uma corda inextensível de massa
desprezível passando por uma polia sem atrito. Os blocos estão
parados. Não há atrito. Temos theta 1 = 0,07 radianos. Qual é o ângulo theta 2
em radianos?
Ver solução completaQuestão 22
(Capítulo 9.1 – Exercício 71) O sistema mostrado na figura consiste em um bloco de colocado sobre uma prateleira horizontal sem atrito. Este bloco está preso a um cordão que passa por uma polia e tem sua outra extremida presa a um bloco pendente . A polia é um disco uniforme de de raio e de massa. Determine a aceleração de cada bloco e as tensões no cordão.

Questão 24
Um pulso, se movendo em uma corda esticada com tensão , é descrita pela função de onda:
- Faça um gráfico de como função de .
- Qual o valor da magnitude da velocidade de propagação do pulso e sua direção?
- Calcule a velocidade transversal de um dado ponto da corda num instante
- Determine a potência instantânea associada a esse pulso e mostre que ela é sempre maior ou igual a zero.
Questão 25
(Cap 4 – Ex 70) Duas caixas de são arrastadas sobre uma superfície horizontal sem atrito com uma aceleração constante de , como mostrado na Figura 4-53. Cada corda tem uma massa de . Encontre a magnitude da força e a tensão nas cordas nos pontos A, B e C.
Ver solução completaQuestão 26
Um balão está preso a um bloco por meio de um fio ideal (massa desprezível e inextensível). A massa do bloco é de . A tensão (módulo) no fio entre o bloco e o balão é de de 30N. O ventor arrasta o balão de modo que o fio faz um ângulo em relação a vertical (ver figura abaixo). Assuma que o módulo da aceleração da gravidade local é . Assuma ainda que o bloco é pequeno, de maneira que a força do vento sobre o bloco é desprezível. A figura mostra o vetor velocidade inicial do bloco cujo módulo é de.
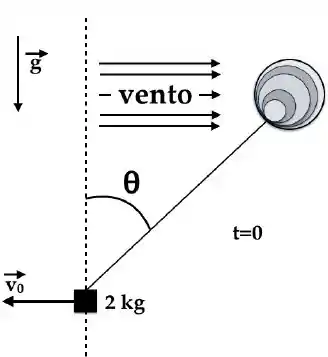

Questão 27
Dois objetos, cada um com peso , estão pendurados conforme mostrado na figura. As polias e cordas têm massa desprezível, e não há atrito na polia. A leitura no dinamômetro será de:

(A) .
(B) Maior do que , mas menor do que .
(C) Menor do que .
(D)
(E) Zero, já que a força resultante sobre ele é nula.
Ver solução completaQuestão 28
Um corpo com massa é mantido suspenso por dois cabos que exercem forças de tração de módulos e , conforme a figura ao lado. Com o eixo horizontal e o eixo vertical, qual das seguintes afirmações é correta?
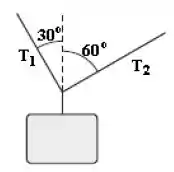
(A)
(B)
(C)
(D)
(E) É necessário conhecer a massa do corpo para comparar as trações.
Ver solução completaQuestão 29
Um bloco de de massa está pendurado na extremidade de uma corda uniforme de de comprimento e com massa igual a . Este sistema desce verticalmente mediante a aplicação de uma força de módulo igual a na extremidade livre da corda, como mostra a figura. Qual é o módulo da força exercida nos extremos da corda nos pontos A e B, respectivamente?
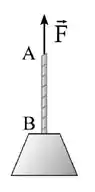
(A) e
(B) e
(C) e
(D) e
(E) e
Ver solução completaQuestão 30
Uma cabine de elevador e sua carga têm uma massa combinada de . Encontre a tensão do cabo de sustentação quando a cabine, originalmente descendo a , é levado ao repouso com aceleração constante em uma distância de .
Ver solução completaQuestão 31
Na figura abaixo, três caixas são conectadas por cordas, uma das quais passa por uma polia de atrito e massa desprezíveis. As massas das caixas , , . Quando o conjunto é liberado a partir do repouso, (a) qual é a tensão da corda que liga a e (b) que distância percorre nos primeiros (supondo que não atinja a polia)?

Questão 32
Um pai de massa brinca com seu filho de massa na superfície horizontal de um lago congelado, onde o atrito pode ser desprezado; considere . Cada um segura uma das extremidades de uma corda leve e comprida. Eles devem puxar a corda para conseguir pegar uma bola, colocada na metade da distância entre os dois. Qual a afirmação é verdadeira quando ambos puxam a corda?
- O resultado dependerá do esforço que cada um fará.
- O pai, alcançará a bola primeiro.
- O filho alcançará a bola primeiro, qualquer que seja seu esforço.
- Os dois sempre alcançarão a bola ao mesmo tempo.
- Nenhuma das afirmações anteriores.
Questão 33
Um sistema consiste de um objeto de peso que é sustentado por três cordas, como mostrado. As trações nas cordas são , e . Quais dos seguintes são valores corretos de e ?:
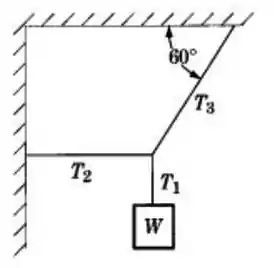
Questão 34
Dois blocos homogêneos e em forma de paralelepípedo, de massas e estão apoiados num piso e formam um sistema conforme a figura ao lado. Por meio de um cordão, deseja-se puxar e imprimir um movimento retilíneo uniformemente acelerado ao sistema, inicialmente em repouso. Considerando que o coeficiente de atrito cinético entre a superfície de B e a do piso vale ; que entre as superfícies de A e de B vale ; que e que o operador puxa o bloco B com uma força , calcule:
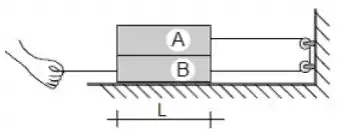
b) A tração na corda.
Ver solução completaQuestão 35
A figura ao lado ilustra uma viga homogênea de peso P. A viga está sustentada na posição horizontal por uma dobradiça e por um cabo, que forma um ângulo em relação à direção da viga, como ilustrado ao lado. Quais são o módulo e o sentido da força horizontal que a dobradiça exerce sobre a viga?
a)
b)
c)
d)
e)
f)
g)
h)
i) 0
Ver solução completaQuestão 36
Os blocos A, B e C possuem mesma massa e repousam em uma superfície horizontal sem atrito. Os três são puxados por uma força horizontal de mesmo módulo e estão presos à uma parede vertical por um fio ideal conforme mostra a figura a seguir.
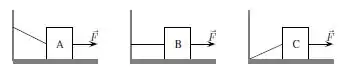
Considerando o módulo das forças normais exercida pelas superfícies sobre os blocos é correto afirmar que:
(a)
b)
(c)
(d)
(e)
(f)
(g)
Ver solução completaQuestão 37
Os dois blocos da figura e estão conectados por fio de massa desprezível. Estes blocos são erguidos verticalmente mediante a aplicação de uma força no bloco . Em um instante após o início do movimento, o módulo da força é reduzido para . A partir deste instante, qual é a tensão no fio?
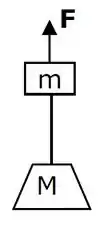
A)
B)
C)
D)
E)
Ver solução completaQuestão 38
Em um conhecido restaurante de Barão Geraldo, uma mini-bicicleta de massa percorre uma corda próxima ao teto, que está fixada nas paredes. No meio do percurso, a corda forma um ângulo com a horizontal, conforme figura.
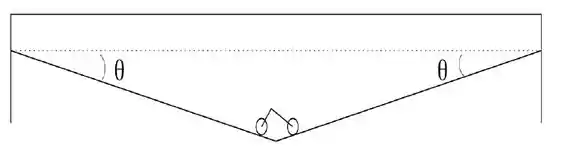
Qual a tensão que a corda exerce na parede?
a.
b.
c.
d.
e.
Ver solução completaQuestão 39
Três macacos A, B e C, de mesma massa, estão pendurados em repouso, cada um em um cipó, com os cipós amarrados em um galho de árvore. Em um dado instante o macaco A sobe em seu cipó com velocidade constante, o macaco B sobe no seu com aceleração constante e o macaco C desce no seu com aceleração constante para baixo. Considerando que os cipós sejam fios ideais, que os movimentos aconteçam na vertical e sabendo que as acelerações mencionadas não são nulas, e denotando por , e as tensões nos cipós dos respectivos macacos A, B e C, podemos dizer que:
(a)
(b) e
(c)
(d)
(e) e
Ver solução completaQuestão 41
Uma pequena esfera de massa m é presa na extremidade de um fio ideal de comprimento ` que tem sua outra extremidade presa a um ponto no teto, formando um pêndulo, como indicado na figura. A esfera é solta de uma posição horizontal, passando a se movimentar pela trajetória como a indicada.
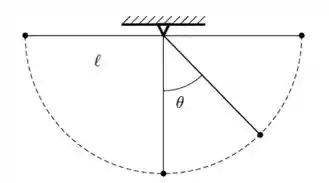
São feitas as seguintes observações sobre o movimento
do pêndulo:
I) Quando na posição mais baixa, a componente tangencial da aceleração possui seu valor máximo.
II) Quando a massa m passa pela posição mais baixa, temos que a tração feita pelo fio sobre a
massa é máxima.
III) A massa m descreve um movimento circular uniforme pois a resultante das forças é a centrípeta.
Quais das afirmações acima estão incorretas:
(a) I) e III)
(b) Apenas I)
(c) Apenas II)
(d) Apenas III)
(e) I) e II)
(f) II) e III)
Ver solução completaQuestão 42
3. Um caixote de massa é puxado por meio de uma corda (como mostra a figura abaixo à esquerda) com uma velocidade constante. A tração na corda é e o ângulo entre a corda e a horizontal é .
e) Qual seria a aceleração do caixote se o coeficiente de atrito baixasse, repentinamente, para a metade do seu valor?
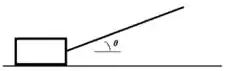
Questão 43
3. Um caixote de massa é puxado por meio de uma corda (como mostra a figura abaixo à esquerda) com uma velocidade constante. A tração na corda é e o ângulo entre a corda e a horizontal é .
b) Calcule a força que o solo exerce no caixote.
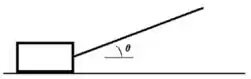
Questão 44
Os dois blocos na figura abaixo estão conectados por uma corda pesada e uniforme com massa de . Uma força de é aplicada para cima, como mostrado.
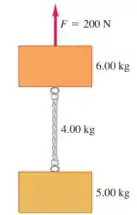
(d) Qual é a tensão no ponto médio da corda?
Ver solução completaQuestão 45
3. Um caixote de massa é puxado por meio de uma corda (como mostra a figura abaixo à esquerda) com uma velocidade constante. A tração na corda é e o ângulo entre a corda e a horizontal é .
c) Calcule o coeficiente de atrito entre o solo e o caixote.
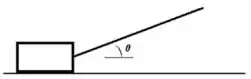
Questão 46
(Cap 4 – Ex 67) Uma caixa de massa está sobre uma estante horizontal sem atrito e presas por fios a caixas de massas e , como mostra a Figura 4-51. As duas polias são sem atrito e sem massa. O sistema é largado do repouso. Após a largada, encontre
(a) a aceleração de cada uma das caixas e
(b) a tensão em cada fio.
Ver solução completaQuestão 47
3. Um caixote de massa é puxado por meio de uma corda (como mostra a figura abaixo à esquerda) com uma velocidade constante. A tração na corda é e o ângulo entre a corda e a horizontal é .
a) Escolha um referencial e desenhe um diagrama das forças que atuam sobre o caixote.
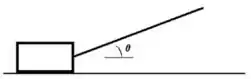
Questão 48
3. Um caixote de massa é puxado por meio de uma corda (como mostra a figura abaixo à esquerda) com uma velocidade constante. A tração na corda é e o ângulo entre a corda e a horizontal é .
d) Calcule o trabalho realizado por cada uma das forças em um deslocamento do caixote de D metros
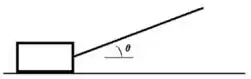
Questão 49
Na figura ao lado dois blocos de mesma massa estão ligados por uma corda de massa desprezível, que passa por uma polia em formato de disco com raio e massa . A corda não escorrega na polia, e não há atrito no eixo da polia. Porém, existe atrito cinético entre a mesa e o bloco que escorrega. Quando o sistema é liberado a partir do repouso, a polia gira de em , e a aceleração dos blocos e da polia são constantes.
c) Quais as trações e nos dois lados da corda?
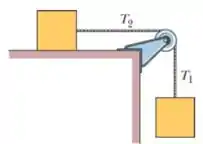
Questão 50
Um trem possui três vagões de massas , e ,ligados entre si por cabos ideais. O trem percorre um trecho retilíneo da ferrovia com aceleração constante , da esquerda para a direita, como mostra a figura.
O módulo da força que o cabo que liga o vagão de massa ao de exerce sobre vagão de massa é igual a
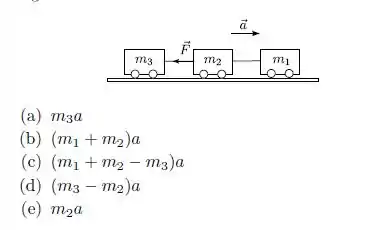
Questão 52
Considere o sistema da figura ao lado. A corda e a polia possuem massas desprezíveis, a corda é inextensível e a polia não possui atrito em seu eixo. O coeficiente de atrito cinético entre o bloco de massa M e o topo da mesa é . Os blocos são liberados a partir do repouso e começam a se acelerar. Dê respostas em termos de e .
3) a tensão dos dois lados da corda e

Questão 53
(Cap 4 – Ex 53) Seu carro atolou na lama. Você está sozinho, mas tem uma corda longa e forte. Tendo estudado física, você amarra a corda fortemente a um poste telefônico e puxa de lado, como mostra a Figura 4-42.
(a) Encontre a força exercida pela corda sobre o carro, quando o ângulo é e você está puxando com uma força de , mas o carro não se move.
(b) Quão forte deve ser a corda se é necessária uma força de para mover o carro quando é
Ver solução completaQuestão 54
(Cap 4 – Ex 83) Se uma das massas da máquina de Atwood da Figura 4-60 é , quanto deve valer a outra massa de forma a que o deslocamento de cada massa, durante o primeiro segundo após a largada, seja Suponha uma polia sem massa e sem atrito e um fio sem massa.
Ver solução completaQuestão 55
(Cap 4 – Ex 82) O aparato da Figura 4-60 é chamado de máquina de Atwood e é usado para medir a aceleração de queda livre medindo-se a aceleração dos dois blocos ligados pelo fio que passa pela polia. Suponha uma polia sem massa e sem atrito e um dio sem massa.
(a) Desenhe o diagrama de corpo livre de cada bloco.
(b) Use os diagramas de corpo livre e as leis de Newton para mostrar que a magnitude da aceleração de cada bloco e que a tensão no fio são e .
(c) Estas expressões fornecem resultados plausíveis se no limite e no limite ? Explique.
Ver solução completaQuestão 56
Um bloco de massa é puxado ao longo de uma superfície, lisa e horizontal, por uma corda de massa sobre a qual se exerce uma força horizontal . Determine as acelerações do bloco e da corda e a força exercida pela corda sobre o bloco. Qual é o valor de se desprezarmos em confronto com ?
Ver solução completaQuestão 57
Um corpo de massa , repousa sobre um outro de massa , que por sua vez está sobre uma superfície horizontal sem atrito. Uma força atua sobre conforme mostra a figura .
a) Sendo sem atrito a superfície entre os dois corpos, determinar a aceleração de cada um deles;
Ver solução completaQuestão 58
Um corpo de massa , repousa sobre um outro de massa , que por sua vez está sobre uma superfície horizontal sem atrito. Uma força atua sobre conforme mostra a figura .
b) Admitindo que a superfície entre os corpos seja suficientemente grosseira para que não escorre sobre , determinar a aceleração dos dois corpos;
Ver solução completaQuestão 59
Um corpo de massa , repousa sobre um outro de massa , que por sua vez está sobre uma superfície horizontal sem atrito. Uma força atua sobre conforme mostra a figura .
c) Determinar a força resultante que age sobre cada corpo em (b);
Ver solução completaQuestão 60
(Cap 4 – Ex 52) Para o sistema das Figuras 4-41a, 4-41b e 4-41c, encontre as massas e as tensões desconhecidas.
Ver solução completaQuestão 61
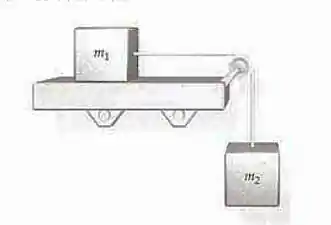
(Cap 5 – Ex 132) Um bloco de massa está sobre uma mesa horizontal. O bloco está preso a um bloco de ( através de um fio leve que passa por uma polia, sem massa e sem atrito, na beirada da mesa. O bloco de massa balança a do chão (Figura abaixo), O sistema é largado do repouso em e o bloco de atinge o chão em , O sistema é, agora, recolocado em sua configuração inicial e um bloco de é colocado sobre o bloco de massa Largado do repouso, o bloco de agora atinge o chão após . Determine a massa e o coeficiente de atrito cinético entre o bloco de massa e a mesa.
Questão 62
Dois trabalhadores puxam horizontalmente uma caixa pesada, mas um puxa duas vezes mais que o outro. A tração maior é direcionada para 25.0°a oeste do norte, e a resultante dessas duas trações é de 350,0 N diretamente para o norte. Use componentes vetoriais para encontrar a magnitude de cada um desses puxões e a direção do menor puxão.
Ver solução completaQuestão 63
(Capítulo 5.9 – Exercício 51) Na Fig. 5-48, três blocos conectados são puxados para a direita sobre uma mesa horizontal sem atrito por uma força de módulo . Se , e , calcule (a) o módulo da aceleração do sistema, (b) a tensão e (c) a tensão

Questão 64
(Capítulo 5.9 – Exercício 41) Um elevador que pesa move-se para cima. Qual é a tensão do cabo do elevador se a velocidade (a) está aumentando a uma taxa de e (b) está diminuindo a uma taxa de ?
Ver solução completaQuestão 65
(Capítulo 5.9 - Exercício 50) A Fig. 5-49 mostra quatro pinguins que estão sendo puxados sobre gelo muito escorregadio (sem atrito) por um zelador. As massas de três pinguins e as tensões em duas das cordas são , , , e . Determine a massa do pinguim , que não é dada.
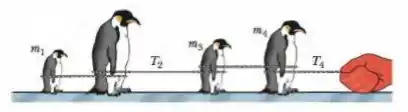
Questão 66
(Capítulo 5.9 – Exercício 37) Uma esfera com uma massa de está suspensa por uma corda. Uma brisa horizontal constante empurra a esfera de tal forma que a corda faz um ângulo de com a vertical. Determine (a) a força da brisa sobre a bola e (b) a tensão da corda.
Ver solução completaQuestão 67
(Cap 5 – Ex 76) Um homem de salta para um pátio de concreto de uma janela a de altura. Ele não dobra os joelhos para amortecer o impacto e leva para parar. (a) Qual é a aceleração média desde o instante em que os pés do homem tocam o solo até o instante em que o corpo se imobiliza? (b) Qual é o módulo da força média que o pátio exerce sobre o homem?
Ver solução completaQuestão 68
(Capítulo 5.9 – Exercício 39) Um elevador e sua carga têm uma massa total de . Determine a tensão do cabo de sustentação quando o elevador, que estava descendo a , é levado ao repouso com aceleração constante em uma distância de .
Ver solução completaQuestão 69
(Capítulo 5.7 – Exercício 15) A Fig. 5-33 mostra um arranjo no qual quatro discos estão suspensos por cordas. A corda mais comprida, no alto, passa por uma polia sem atrito e exerce uma força de sobre a parede à qual está presa. As tensões nas cordas mais curtas são , e . Quais são as massas (a) do disco , (b) do disco, (c) do disco C e (d) do disco?
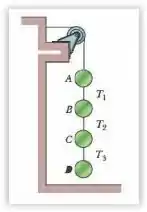
Questão 70
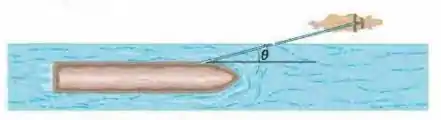
(Capítulo 5.9 – Exercício 48) No passado, cavalos eram usados para puxar barcaças em canais, como mostra a Fig. 5-42. Suponha que o cavalo puxa o cabo com uma força de módulo e ângulo em relação à direção do movimento da barcaça, que se desloca no sentido positivo de um eixo . A massa da barcaça é e o módulo da aceleração da barcaça é . Quais são (a) o módulo e (b) a orientação (em relação ao sentido positivo do eixo ) da força exercida pela água sobre a barcaça?
Questão 71
Um engradado de massa é puxado com velocidade constante por um guincho, numa distância , numa rampa sem atrito, até uma altura acima do ponto de partida.
a. Qual é o módulo da força exercida pelo guincho e qual o trabalho realizado por esta força?
Ver solução completaQuestão 72
Os três blocos da figura abaixo deslizam sobre a superfície horizontal sem atrito. Se a tensão na corda 1 é de , determine o módulo de .
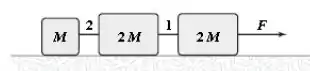
A)
B)
C)
D)
E)
Ver solução completaQuestão 73
(Cap 4 – Ex 50) Uma bola pesando 100 N é mostrada suspensa por um sistema de cordas (Figura 4-39). Quais são as tensões nas três cordas?
Ver solução completaQuestão 74
1) O sistema da Fig. abaixo está em equilíbrio, com a corda do centro exatamente na horizontal. O bloco pesa , o bloco pesa e o ângulo é . Determine (a) a tração , (b) a tração , (c) a tração e (d) o ângulo .
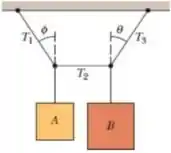
Questão 75
2) A figura mostra uma barra de de comprimento e massa desprezível, suspensa por uma corda , sustentando um peso de no ponto indicado. Sabendo que a barra se apoia sem atrito nas paredes do vão, qual a razão entre a tensão na corda e a reação na parede no ponto , no equilíbrio estático?
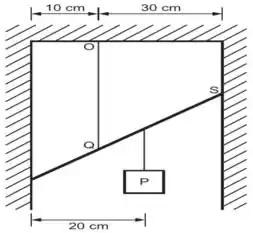
Questão 76
(Cap 4 – Ex 49) Na figura 4-38a, um bloco de 0,500 kg está suspenso pelo ponto central de um fio de 1,25 m. As extremidades do fio estão presas ao teto em pontos separados de 1,00 m.
(a) Qual é o ângulo que o fio forma com o teto?
(b) Qual é a tensão no fio?
(c) O bloco de 0,500 kg é removido e dois blocos de 0,250 kg são presos ao fio de forma tal que os comprimentos dos três segmentos do fio são iguais (Figura 4-38b). Qual é a tensão em cada segmento do fio?
Ver solução completaQuestão 77
Um objeto de massa é puxado para cima, na vertical, por meio de um fio ideal. Sabe-se que a tensão máxima que o fio suporta, sem se romper, é (com ). Qual é a maior aceleração que o corpo pode ter sem que o fio arrebente?
(a)
(b)
(c)
(d)
(e)
(f)
Ver solução completaQuestão 78
Dois corpos P e Q em uma superfície horizontal sem atrito estão ligados por uma corda de massa desprezível. A massa de P é maior do que a de Q. Uma força horizontal de módulo é aplicada sobre Q como mostrado na figura, acelerando os dois corpos para a direita. O módulo da tração exercida pela corda sobre P é:
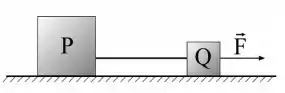
(A) Zero.
(B) Maior do que zero, porém menor do que o módulo de F.
(C) Igual ao módulo de F.
(D) Maior do que o módulo de F.
(E) Menor do que o módulo da tração da corda sobre Q.
Ver solução completaQuestão 79
Três macacos , e , de mesmo peso, estão pendurados em repouso, cada um em um cipó, com os cipós amarrados em um galho de árvore. A partir de um dado instante o macaco sobe em seu cipó com velocidade constante, o macaco sobe no seu com aceleração para cima constante e o macaco desce no seu com aceleração para baixo constante. Supondo que os cipós sejam fios ideiais (inextensíveis com massa desprezível), que os movimentos se processem na vertical, que as acelerações mencionadas não sejam nulas, e denotando por , e as tensões nos cipós dos respectivos macacos , e , podemos dizer que
- e
Questão 80
Na figura ao lado, uma barra horizontal fina AB, de massa desprezível e comprimento , é presa a uma dobradiça em uma parede vertical no ponto A e sustentada em B por um fio ideal fino BC. O fio faz um ângulo com a horizontal. Um bloco de peso P pode ser movido para qualquer posição ao longo da barra, sendo a sua posição definida pela distância desde a parede até o seu centro de massa (veja a figura).
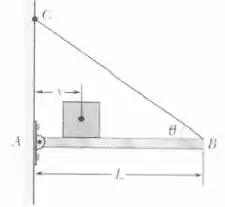
Sabe-se que a aceleração da gravidade no local é constante e aponta para baixo, agindo na direção paralela à parede vertical. Para tal situação, calcule:
- A tensão no fio. Expresse sua resposta em termos de , , e .
- A componente horizontal da força exercida sobre a barra pelo pino da dobradiça em . Expresse sua resposta em termos de , , e .
- A componente vertical da força exercida sobre a barra pelo pino da dobradiça em . Expresse sua resposta em termos de , e .
Questão 81
Dois blocos de mesma massa estão conectados por uma corda horizontal sem massa e se encontram em repouso sobre uma mesa sem atrito. Quando um dos blocos for puxado por uma força externa horizontal, , qual é a razão entre as forças resultantes que atuam sobre os blocos?
Nenhuma das respostas acima.
Ver solução completaQuestão 82
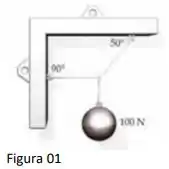
Uma bola pesando 100 N é mostrado na Figura 1 e está suspensa por um sistema de cordas. Determine as tens��es nas três cordas.
Questão 83
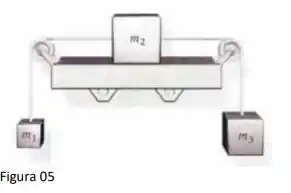
Uma caixa de massa 𝑚2 = 3,5𝑘𝑔 está sobre uma estante horizontal sem atrito e presa por fios a caixas de massa 𝑚1 = 1,5𝑘𝑔 e 𝑚3 = 2,5𝑘𝑔, conforme figura 5. As duas polias são sem atrito e sem massa. O sistema é solto do repouso. Após a largada, encontre
(a) a aceleração de cada uma das caixas
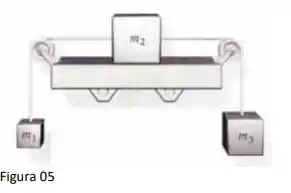
Questão 84
Uma caixa de massa 𝑚2 = 3,5𝑘𝑔 está sobre uma estante horizontal sem atrito e presa por fios a caixas de massa 𝑚1 = 1,5𝑘𝑔 e 𝑚3 = 2,5𝑘𝑔, conforme figura 5. As duas polias são sem atrito e sem massa. O sistema é solto do repouso. Após a largada, encontre
(b) a tensão em cada fio
Questão 85
Considere e o coeficiente de atrito estático entre o bloco e o plano é .
(a) Encontre a faixa de valores possíveis para para qual o sistema permanecerá em equilíbrio estático.

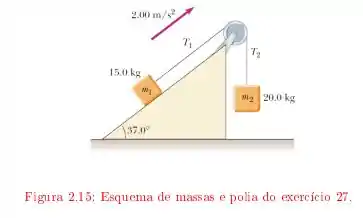
Questão 86
Dois blocos estão ligados por um fio de massa desprezível passando sobre uma polia de raio e momento de inércia . O bloco sobre o plano inclinado sem atrito está subindo com uma aceleração constante de .
Determine e , as duas tensões nas duas partes do fio.
Questão 87
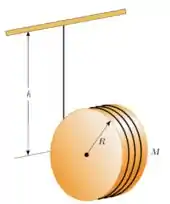
37. Um cilindro uniforme de raio e massa tem um fio enrolado sobre a sua superfície. O disco é solto do repouso com o fio vertical e com sua extremidade superior presa a uma barra fixa.
(a) Qual é a tensão no fio?
Questão 88
Na figura, a corda ideal suporta um homem pendurado num ponto equidistante dos dois apoios ( e ), a certa altura do solo, formando um ângulo de .

A razão entre as intensidades da tensão na corda () e do peso do homem () corresponde a:
A)
B)
C)
D)
E)
Ver solução completaQuestão 89
A figura abaixo dois blocos, um dos quais está em cima de uma mesa, ligado a o outro bloco a partir de uma corda de massa desprezível que passa por uma poia de baixo atrito. O segundo bloco, de inércia , está suspenso no ar. Considere que o coeficiente de atrito estático entre o bloco de inércia e a mesa vale .
- Faça o diagrama de corpo livre para cada um dos blocos, indicando todas as forças que atuam em cada um deles.
- Sabendo que a inércia do bloco suspenso no ar é , determine qual deve ser a inércia do bloco que está sobre a mesa para que o sistema fique em repouso.
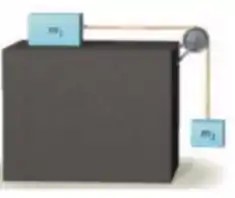
Questão 90
Três caixas de massa , unidas por fios sem massa, são puxadas por uma força constante aplicada à massa da extremindade direita, conforme a figura abaixo. Não há atrito entre as caixas e a superfície horizontal. Sejam e as tensões dos fios e indicados na figura. Determine a razão .

Questão 91
Um peixe de é pesado usando duas molas com escalas, cada uma de massa desprezível, como mostrado na figura. Considere o peixe e as molas estão em repouso perto da superfície da Terra e que .
Qual será a leitura nas escadas de cada balança?
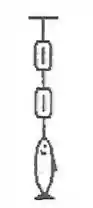
- A escala da mola de baixo marca e a de cima marca zero.
- Cada escala marca .
- A escala da mola de cima marca e a de baixo marca zero.
- As escalas terão valores diferentes, mas a soma delas será .
- Cada escala irá marcar .
Questão 92
Um acelerômetro simples é construído suspendendo-se um corpo de massa por um fio de tamanho que está ligado ao teto do carro. Quando o carro acelera, o fio faz ângulo constante com a vertical.
(a) Desenhe o diagrama de forças atuando no corpo.
(b) Escreva as equações de movimento para o corpo.
(c) Supondo que o fio tenha massa desprezível comparada com , mostre que a expressão da aceleração é função de e que é independente de e .
(d) Se o ângulo medido é , calcule a aceleração do carro.
Dados: , e
Ver solução completaQuestão 93
Um carretel é livre para girar em torno de um eixo fixo, e um cordão enrolado em torno do seu eixo faz com que ele gire no sentido anti-horário como indicado na . No entanto, se o carretel é colocado sobre uma mesa horizontal , com o ângulo entre o fio e a horizontal igual ao da , e se há força de atrito suficiente entre ele e a mesa, podemos dizer que tal carretel:
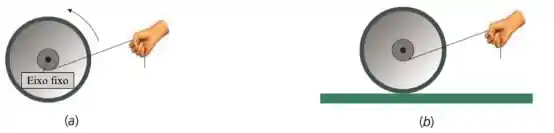

Questão 94
Um corpo de massa , repousa sobre um outro de massa , que por sua vez está sobre uma superfície horizontal sem atrito. Uma força atua sobre conforme mostra a figura .

Qual é o módulo, a direção e o sentido da força de contato exercida pelo corpo de massa sobre o corpo de massa ?
Ver solução completaQuestão 95
Uma esfera com uma massa de está suspensa por uma corda. Uma brisa horizontal constante empurra a esfera (com velocidade constante) de tal forma que a corda faz um ângulo de com a vertical. Determine:
A tensão da corda;
Ver solução completaQuestão 96
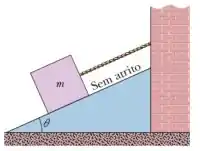
Na figura a massa do bloco é e o ângulo é . Determine:
a tensão na corda;
Questão 97
Uma esfera com uma massa de está suspensa por uma corda. Uma brisa horizontal constante empurra a esfera (com velocidade constante) de tal forma que a corda faz um ângulo de com a vertical. Determine:
a força da brisa sobre a bola;
Ver solução completaQuestão 98
A figura mostra um bloco sobre um plano inclinado sem atrito de ângulo . O bloco está ligado por uma corda de massa desprezível a um outro bloco ( situado sobre um plano inclinado sem atrito de ângulo . A polia não tem atrito e a massa é desprezível. Qual é a tensão da corda?
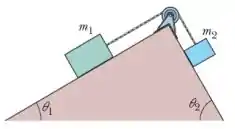
Questão 99
O bloco de e o bloco de estão conectados por uma corda de massa desprezível. A força atua sobre o bloco a força atua sobre o bloco . Qual é a tensão da corda?
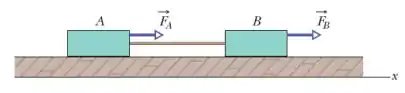
Questão 100
Na figura, uma lata de antioxidante sobre um plano inclinado sem atrito está ligada a uma lata de apresuntado . A polia tem massa e atrito desprezíveis. Uma força vertical para cima de módulo atua sobre a lata de apresuntado, que tem uma aceleração para baixo de Determine a tensão da corda e o ângulo .