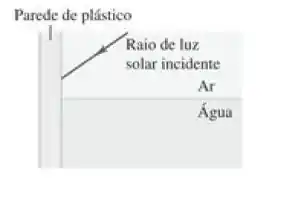
Um raio de luz solar não-polarizada atinge a parede plástica vertical de um tanque de água em um ângulo desconhecido. Parte da luz se reflete na parede e entra na água (Figura 33.60). O índice de refração da parede de plástico é . Se a luz que foi refletida na parede e entrou na água revelar-se totalmente polarizada, qual é o ângulo que esse feixe faz com a normal dentro da água?

A luz que refletiu na parede está totalmente polarizada. Isso quer dizer que a luz incidiu na parede com o ângulo de Brewster. Ou seja, na interface ar-parede, temos

Com isso

Esse é o ângulo de incidência na parede, que é igual ao ângulo de reflexão.

Quando o raio foi incidir na superficie de água, o ângulo de incidência será seu complementar

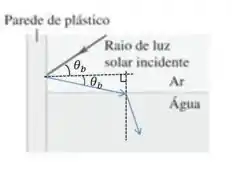
Aplicando a lei de snell na interface ar-agua:

Com isso: