Um retângulo rígido ABCD, com e , está submetido a cinco forças: em , uma força de na direção e sentido , uma força de na direção e sentido , e uma força de segundo a direção e sentido de ; em , uma força de e outra de atuam nas direções e sentidos de e , respectivamente. Determine a força resultante e os momentos relativos aos pontos , e ao centro geométrico.
Passo 1
E aí, beleza?? A figura que ilustra o problema é a seguinte:
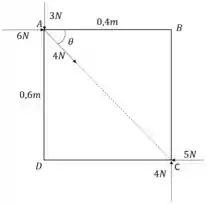
Assim, a força resultante é dada por:
Portanto:
Passo 2
O torque em relação ao ponto é dado apenas pelas forças aplicadas em . Assim, considerando as linhas de ação das forças:
Aplicando a regra da mão direita:
Passo 3
Em relação ao ponto , devemos considerar as forças cuja linha de ação não passa por esse ponto. Assim, vem:
Portanto, pela regra da mão direita:
Resposta
Agora em relação ao centro, desconsideramos apenas a força diagonal. Portanto:
Pela regra da mão direita: