Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 81

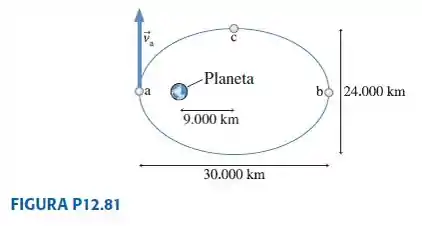
Um satélite descreve a órbita elíptica mostrada. A única força exercida sobre o satélite é a atração gravitacional do planeta. O módulo da velocidade do satélite neste ponto é de 8.000 m/s.

a. Algum torque é exercido sobre o satélite?

b. Qual é o módulo da velocidade do satélite no ponto b?

c. Qual é o módulo da velocidade do satélite no ponto c?

Passo 1

O momento angular do satélite na órbita elíptica é uma constante.

Vamos visualizar:

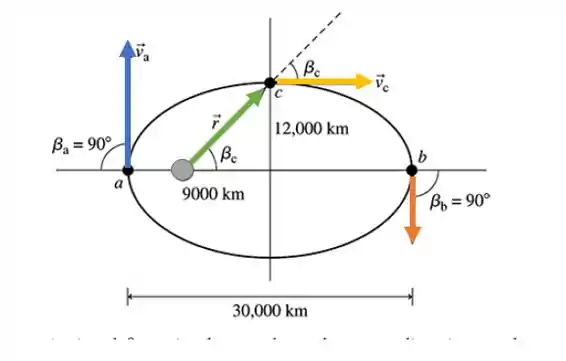
Passo 2

  1. Como a força gravitacional está sempre na mesma direção que a direção do vetor do braço no momento, o torque τ → = r → × F → g é zero em todos os pontos da órbita.

    2. Passo 3

  2. O momento angular do satélite em qualquer ponto da trajetória elíptica é conservado. A velocidade é perpendicular a r →   nos pontos a e b , então β = 90 ° e L = m v r . Então

    3. L b = L a

    ⇒ m v b r b = m v a r a

    Isolando v b :

    v b = r a r b v a

    Passo 4

    Para calcularmos r a fazemos:

    r a = 30,000   k m 2 - 9000   k m = 6000   k m

    E para calcular r b :

    r b = 30,000   k m 2 + 9000   k m = 24,000   k m

    Então, voltando para a equação, v b = r a r b v a , temos que:

    v b = 6000   k m 24,000   k m 8000   m / s = 2000   m / s

    Passo 5

  3. Usando a conservação do momento angular L c = L a , nós temos que:

m v c r c   s e n   β c = m v a r a

⇒ v c = r a r c v a s e n   β c

Uma vez que r c é dado por:

r c = 9000   k m 2 + 12,000   k m 2 = 1,5 × 10 7   m

A partir da figura, vemos que s e n   β c = 12,000 15,000 = 0,80 . Então:

v c = 6000   k m 15,000   k m = ( 8000   m / s ) 0,80 = 4000   m / s

Resposta

  1. Não.
  2. 2000   m / s
  3. 4000   m / s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As extremidades dos dentes de carboneto de uma serra circular estão situadas a uma distância de 8,6 cm do eixo de rotação. a) Quando a serra não está cortando nenhum objeto, suavelocidade angular é de
Um motor elétrico consome 9,0 kJ de energia elétrica em 1,0 min. Se um terço dessa energia é consumida no aquecimento e em outras formas de energia interna do motor e o restante é aprodução do motor,
O motor fornece 175 hp para a hélice de um avião a uma rotação de 2400 rev/min. a) Qual é o torque fornecido pelo motor do avião? b) Qual é o trabalho realizado pelo motor em umarevolução da hélice?
A roda de um esmeril de 1,50 kg possui forma cilíndrica com raio igual a 0,100 m. a) Qual deve ser o torque constante capaz de levá-la do repouso a uma revolução angular de 1200 rev/min em 2,5 s? b) Q
A hélice propulsora de um avião possui comprimento de 2,08m (de uma extremidade a outra) e sua massa é de117k g . Logo no início do funcionamento do motor, ele aplica um torquede 1950N ⋅ m na hélice,