Exercícios de Torque - Lista de Exercícios Resolvida
Questão 1
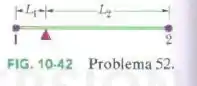
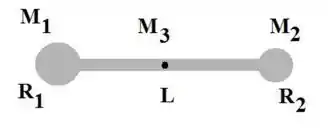
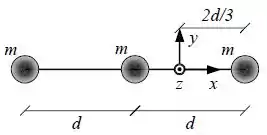
A figura abaixo mostra as partículas 1 e 2, ambas de massa , presas às extremidades de uma barra rígida de massa desprezível e comprimento , com e . A barra é mantida horizontalmente no fulcro até ser liberada. Qual é o módulo da aceleração inicial (a) da partícula 1 e (b) da partícula 2?
Questão 2
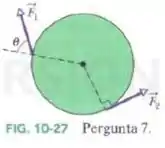
Na Fig. 10-27, duas forças e , agem sobre um disco em torno do centro como um carrossel. As forças mantêm os ângulos indicados durante a rotação, que ocorre no sentido anti-horário e com velocidade angular constante. Precisamos diminuir o ângulo de sem mudar o módulo de , (a) Para manter a velocidade angular constante, devemos aumentar, diminuir ou manter constante o módulo de ? (b) A força tende a girar o disco no sentido horário ou anti-horário? (c) E a força ?
Questão 3
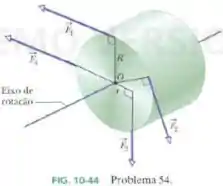
Duas rodas, uma de raio e outra de raio , são fixadas uma sobre à outra de modo concêntrico e são livres para rodar em torno de seu eixo de simetria. Como mostrado abaixo, quatro forças são exercidas tangencialmente às rodas.
Qual é a magnitude do torque resultante?
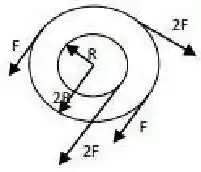
a) zero
b)
c)
d)
e)
Ver solução completaQuestão 4
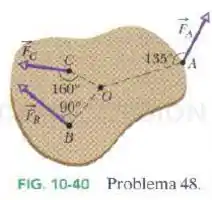
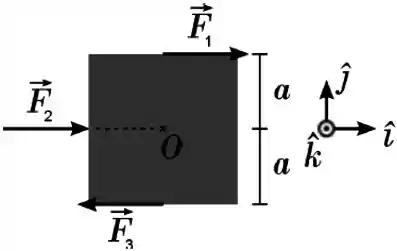
O corpo da Fig. 10-40 tem um eixo que passa por e é perpendicular ao papel. Três forças agem sobre ele: no ponto , a de ; em , a de ; e em , a de . Qual é o torque resultante em relação a ?
Questão 5
Um ciclista de apoia toda a sua massa em cada movimento do pedal para baixo enquanto pedala em uma estrada íngreme. Suponha que o diâmetro da circunferência descrita pelo pedal é de e determine o módulo do torque máximo exercido pelo ciclista em relação ao eixo de rotação dos pedais.
Ver solução completaQuestão 6
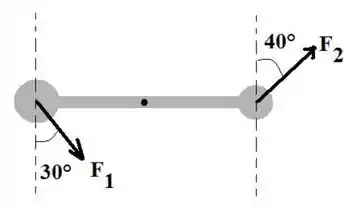
A figura abaixo mostra uma vista superior de uma barra horizontal que gira em torno de um eixo sob a ação de duas forças horizontais, e , com fazendo um ângulo com a barra. Ordene os seguintes valores de de acordo com o módulo da aceleração angular da barra, do maior para o menor: e .
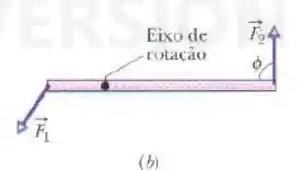
Questão 7
Em termos dos vetores unitários, qual é o torque em relação à origem a que está submetida uma partícula localizada nas coordenadas () se esse torque se deve (a) a uma força de componentes e (b) a uma força de componentes ?
Ver solução completaQuestão 8
Na figura abaixo um cilindro com uma massa de pode girar em torno de seu eixo central, que passa pelo ponto . As forças mostradas têm os seguintes módulos: , , e . As distâncias radiais são e . Determine (a) o módulo e (b) a orientação da aceleração angular do cilindro. (Durante a rotação, as forças mantêm seus ângulos em relação ao cilindro.)
Questão 9
(Cap 10 – Ex 93) Na Fig. 10-56, uma roda com de raio é montada em um eixo horizontal sem atrito. Uma corda de massa desprezível é enrolada na roda e presa a uma caixa de que escorrega sobre uma superfície sem atrito com uma inclinação em relação à horizontal . A caixa escorrega para baixo com uma aceleração de . Qual é o momento de inércia da roda em relação ao eixo?
Ver solução completaQuestão 10
13. Um disco homogêneo de raio e massa está fixo em uma de suas extremidades a uma parede vertical, conforme a figura abaixo. O disco gira, sem atrito, ao redor do eixo fixo que passa pelo ponto O é perpendicular ao plano , sendo abandonado com velocidade inicial nula quando o centro de massa está na altura do eixo de rotação. O módulo do vetor aceleração angular do disco no instante em que ele é abandonado, em , é:

Questão 11
A força age sobre uma partícula cujo vetor posição é . Qual é
o torque em relação à origem a que está submetida a partícula, em termos dos vetores unitários ;
e o ângulo entre e ?
Ver solução completaQuestão 12
Duas chapas quadradas (1) e (2) de lados iguais têm massas e , respectivamente, e estão presas em uma parede vertical pelos seus centros e , em pinos em torno dos quais podem girar sem atrito. Aplica-se em cada uma delas uma mesma força , vertical de baixo para cima, como mostra a figura. A opção que correlaciona os módulos de seus torques e e suas acelerações angulares e imediatamente após a aplicação de é:
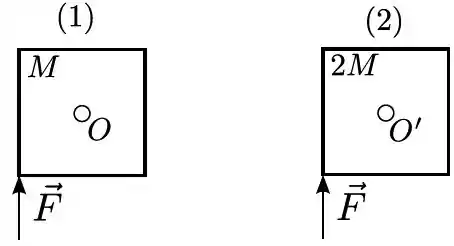
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 13
Um disco homogêneo de massa e raio encontra-se sobre uma mesa horizontal completamente lisa, sem estar preso a ela. Em um dado instante duas forças estão aplicadas tangencialmente na beirada do disco, uma em um ponto diametralmente oposto ao ponto de aplicação da outra. Sabendo que o momento de inércia do disco relativo ao eixo perpendicular a ele que passa pelo seu centro de massa é , e denotado por e os módulos respectivos da aceleração do centro de massa do disco e da aceleração angular de rotação em torno do eixo no instante considerado, podemos dizer que:
- e ;
- e ;
- e ;
- e ;
- e
Questão 14
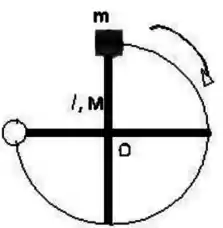
Uma partícula de massa está girando em torno de um eixo (perpendicular a página) com movimento de rotação uniformemente variando com aceleração , como mostra a figura; vista de cima. O raio de trajetória é e o vetor aceleração da partícula tem a sua direção formando um ângulo com a direção radial. Num dado instante ela tem velocidade angular e aceleração angular . Pode-se afirmar que:
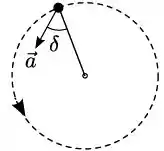
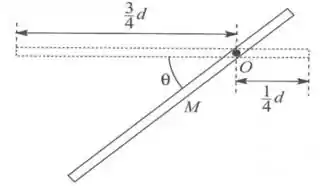
- ;
- ;
- ;
- ;
- ;
Questão 15
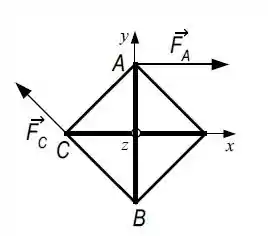
Três forças, , e , de mesmo módulo , agem sobre uma placa quadrada de lado , como ilustra a figura; as forças estão no plano da placa. Usando os unitários e indicados na figura, indique a opção correta para o torque total dessas forças relativo ao centro da placa.
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 16
Em um certo instante, a força age sobre um objeto de cujo vetor posição é e cujo vetor velocidade é . Em relação à origem e em termos dos vetores unitários, qual é
o momento angular do objeto e
o torque que age sobre o objeto?
Ver solução completaQuestão 17
As cinco forças mostradas na figura, todas de mesmo módulo, agem sobre uma placa quadrada que pode girar em torno do ponto . Ordene as forças em ordem crescente do módulo do torque que cada uma exerce em relação ao ponto .
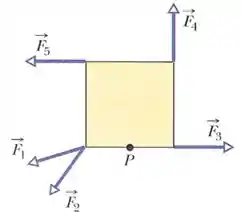
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 18
Uma força atuando sobre uma peça de uma máquina é dada pela expressão . O vetor da origem ao ponto onde a força é aplicada é dado por .
b) Use a regra da mão direita para determinar a direção e sentido do torque.
Ver solução completaQuestão 19
Uma força atuando sobre uma peça de uma máquina é dada pela expressão . O vetor da origem ao ponto onde a força é aplicada é dado por .
c) Determine algebricamente o vetor torque produzido por essa força. Verifique se a direção e sentido do torque são iguais aos obtidos no item .
Ver solução completaQuestão 20
Um operário está usando uma chave de boca para afrouxar uma porca. A ferramenta tem de comprimento, e ele exerce uma força de sobre a extremidade do cabo formado um ângulo de com o cabo.
Qual é o torque máximo que ele pode exercer com essa força, e como a força deve ser orientada?
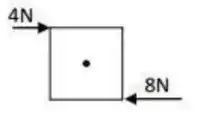
Ver solução completaQuestão 21
Uma roda de esmeril de possui forma cilíndrica com raio igual a .
b) Que ângulo ela girou durante esse intervalo de tempo?
Ver solução completaQuestão 22
Uma roda de esmeril de possui forma cilíndrica com raio igual a .
a) Qual deve ser o torque constante capaz de levá-la do repouso a uma revolução angular de em ?
Ver solução completaQuestão 23
(Cap 10 – Ex 87) Uma roda de de raio está montada em um eixo horizontal sem atrito . O momento de inércia da roda em relação ao eixo é . Uma corda de massa desprezível está enrolada na roda e presa a um bloco de que escorrega em uma superfície horizontal sem atrito. Se uma força horizontal de módulo é aplicada ao bloco, como na Fig. 10-53, qual é o módulo da aceleração angular da roda? Suponha que a corda não desliza em relação à roda.
Ver solução completaQuestão 24
A turbina e partes associadas que giram em um motor a jato tem um momento de inércia total de . A turbina é acelerada uniformemente a partir do repouso até atingir uma velocidade angular de em um tempo de . Encontre o torque resultante para imprimir esse movimento à turbina.
Ver solução completaQuestão 25
Uma roda com momento de inércia é colocada em um eixo e é livre para girar sem atrito. Qual o torque médio necessário para que a roda passe do repouso a uma velocidade angular de em 2 segundos?
Questão 26
Um disco está livre para girar em torno de um eixo fixo que passa pelo . Uma força de módulo conhecido, , deve ser aplicada no plano do disco. Entre as opções abaixo, a aceleração angular será maior se a força for aplicada:
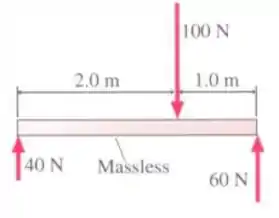
- Tangencialmente, em um ponto a meio caminho entre o eixo e a borda.
- Radialmente, em um ponto a meio caminho entre o eixo e a borda.
- Radialmente, em um ponto da borda.
- Em um ponto da borda, mas nem radialmente nem tangencialmente.
- Tangencialmente, em um ponto da borda.
Questão 27
Em uma gangorra de parque, uma criança de se senta em uma extremidade da gangorra, enquanto uma criança maior, de g, se senta na outra extremidade. Quando a criança menor tira o pé do chão, calcule a intensidade da força Normal do chão no pé da criança maior. Considere que a gangorra se mantem sempre na horizontal.
- Zero.
Questão 28
Um ioiô é formado por dois discos de massa e raio conectados por um eixo de raio de momento de inércia desprezível. Enrolado ao eixo está um fio inextensível de massa desprezível que, ao se desenrolar, não desliza sobre o eixo. O módulo da aceleração do centro de massa do ioiô vale:
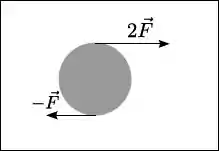
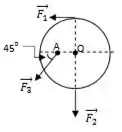
Dados: Momento de inércia de um disco de massa e raio cujo eixo de rotação passa pelo seu centro de massa:
Ver solução completaQuestão 29
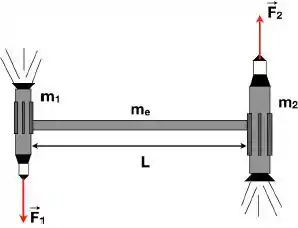
Dois corpos de massa e estão sujeitos à ação da gravidade e são pendurados por cordas naextremidade de uma barra de massa desprezível. A barra é apoiada sobre um ponto distante de uma de suas extremidades e permanece em equilíbrio, como mostrado na figura abaixo. Se a corda de apoio ao bloco é cortada encontre o torque agindo no sistema em relação ao ponto de apoio da barra.
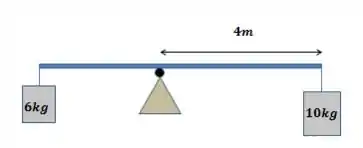
Obs: Alteramos as opções, já que a questão foi anulada.
Ver solução completaQuestão 30
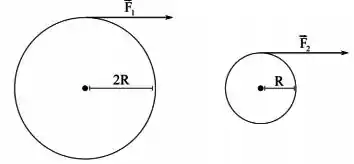
Duas rodas, uma de raio e outra de raio , são fixadas uma sobre à outra de modo concêntrico e são livres para rodar em torno de seu eixo de simetria. Como mostrado abaixo, quatro forças são exercidas tangencialmente às rodas.
Qual é a magnitude do torque resultante?
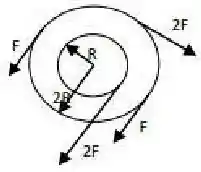
a) zero
b)
c)
d)
e)
Ver solução completaQuestão 31
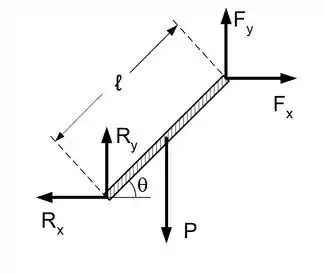
Um ioiô é pendurado ao teto por um fio que não possui massa nem atrito. Ele é liberado verticalmente a partir do repouso como mostra a figura. O seu centro de massa cai de uma altura em relação a sua altura inicial e, durante a queda, o seu centro de massa move-se verticalmente. A afirmativa correta sobre a dinâmica do ioiô durante a queda é:
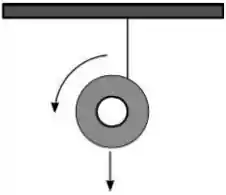
a) tração do fio varia linearmente com o tempo durante a sua queda.
b) em relação ao centro de massa do ioiô o torque resultante é nulo.
c) em relação ao centro de massa do ioiô o torque da tração é nulo.
d) o torque resultante devido às forças peso e tração sobre o ioiô é constante.
e) a força peso não realiza trabalho sobre o ioiô.
Ver solução completaQuestão 32
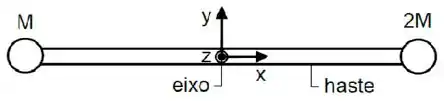
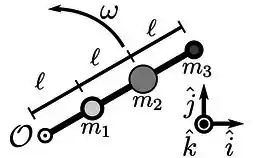
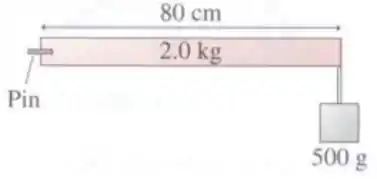
Um sistema é formado por dois corpos, um com massa e o outro com massa , que estão ligados por uma haste rígida sem massa de comprimento . Como mostrado na figura, o sistema pode girar ao redor de um eixo horizontal que atravessa o “Pivot Point”. O sistema está sob a ação da aceleração da gravidade . Quando o sistema é liberado, a haste começa a rodar com uma aceleração angular cuja magnitude é:
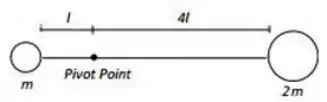
a)
b)
c)
d)
e)
Ver solução completaQuestão 33
Uma roda sólida de massa M, raio R e momento de inércia , rola sem deslizar sobre uma superfíciehorizontal. Uma força horizontal F é aplicada sobre o eixo de rotação da roda e imprime uma aceleração A ao centro de massa da roda. As magnitudes da força F aplicada e a força de atrito da superfície f, respectivamente, são:
- ,
- ,
- ,
Questão 34
Uma haste metálica fina e homogênea, de comprimento e massa , pode girar livremente em torno de um eixo horizontal que a atravessa perpendicularmente em um ponto O distante de uma suas das extremidades, conforme mostrado na figura. A haste é solta a partir do repouso de uma posição horizontal, portanto, estando com sua dimensão maior paralela ao chão.
- Calcule o momento de inércia da haste com respeito ao eixo em torno do qual ela gira.
- Calcule a velocidade angular adquirida pela haste após ela ter caído de um ângulo , conforme indicado na figura.
- Calcule a aceleração da haste após ela ter caído do mesmo ângulo
Dado: Momento de inércia de uma barra de massa e comprimento cujo eixo de rotação passa pelo seu centro de massa:
Ver solução completaQuestão 35
Um disco possui momento de inércia de e está submetido a uma aceleração angular constante de Se o disco partiu do repouso o trabalho realizado nos primeiros segundos pelo torque resultante foi de:
- 0.
Questão 36
Um anel de raio tem massa distribuída uniformemente. Ele é posicionado no plano horizontal, de modo que o eixo seja vertical e apontando pra cima, e atravesse o seu centro de massa. O anel gira com aceleração angular . No instante , ele apresenta velocidade angular
- Faça um desenho mostrando os vetores velocidade angular no instante e a aceleração angular do anel, viso de cima, em Indique se o disco gira no sentido horário ou anti-horário.
- Em que instante o anel terá girado uma revolução completa?
- Em que instante o anel para momentaneamente?
- Calcule o momento de inércia do anel em relação ao eixo
- Qual deve ser o torque(módulo, direção e sentido) aplicado ao anel necessário para o movimento descrito?
Questão 37
Um halter é formado por uma barra de massa desprezível e comprimento que sustenta nas suas extremidades duas esferas, cada uma de massa e raio desprezível. Ele está girando em torno de seu centro de massa. Em 3 revoluções, o halter diminui o módulo de sua velocidade angular de e , com aceleração angular cujo módulo é constante.
- Faça um desenho esboçando qualitativamente os vetores angulares inicial, velocidade angular final e aceleração angular.
- Calcule o módulo da aceleração angular do halter.
- Calcule o intervalo de tempo em que ocorre o decréscimo de velocidade descrito.
- Calcule o momento de inercia do halter.
- Qual deve ser o torque aplicado sobre o halter para provocar o decréscimo de velocidade descrito?
Questão 38
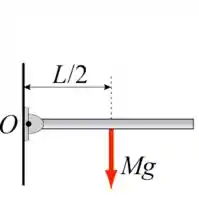
Uma haste uniforme de comprimento e massa pode rodar livremente em torno de um pino passando por uma das extremidades (ponto O). A haste é abandonada na posição horizontal a partir do repouso.
- Qual é a sua velocidade angular quando ela atinge a posição vertical?
- Determine a velocidade linear do centro de massa e a da extremidade da haste quando ela está na posição vertical.
- Qual é o torque na haste e sua aceleração angular em função do ângulo que a haste forma com a posição vertical ?
- O momento angular da haste em relação ao ponto O se conserva? Justifique sua resposta.
Dado: O momento de inércia de uma haste de massa M e comprimento d em relação a um eixo que passa pelo seu centro de massa é
Questão 39
Um homem com os braços junto ao corpo está em cima de uma cadeira giratória que gira sem atrito. Quando o homem estende os braços:
a) A velocidade angular da cadeira aumenta
b) A velocidade angular da cadeira continua a mesma
c) O momento de inércia do homem diminui
d) A energia cinética do sistema aumenta
e) O momento angular do sistema continua o mesmo
Ver solução completaQuestão 40
A hélice propulsora de um avião possui comprimento (de uma extremidade a outra) e massa . Logo no início do funcionamento do motor, ele aplica um torque de na hélice, que começa a se mover a partir do repouso. O momento de inércia da hélice em relação ao eixo perpendicular ao plano da hélice passando pelo seu centro de massa é .
(a) Construir o gráfico do ângulo de rotação em função do tempo , considerando a unidade de em revoluções e do tempo em segundos (). Também construa o gráfico da velocidade angular em função do tempo (). Considere na construção de ambos os gráficos os instantes e .
(b) Qual é o trabalho realizado pelo motor durante as . iniciais? Utilize a unidade do trabalho realizado em Joule .
(c) Qual é a potência média fornecida pelo motor durante as iniciais? Utilize a unidade da potência em Watts .
(d) Qual é a potência instantânea do motor no instante em que a hélice propulsora completa essas .? Utilize a unidade da potência em Watts .
Ver solução completaQuestão 41
Um pêndulo simples é formado por uma partícula de massa ligada a uma corda de comprimento de massa desprezível. Ele está preso num ponto de suspensão O, inicialmente em sua posição vertical e é deslocado de um ângulo , de onde passa a executar um movimento oscilatório. Podemos afirmar que:
a) O vetor aceleração do sistema é constante, uma vez que as forças atuantes possuem módulo constantes.
b) O torque produzido pela força peso calculado a partir do ponto O no instante em que a partícula atinge a posição angular é dado por e é perpendicular ao plano de oscilação do pêndulo.
c) Adotando como referência a posição vertical da partícula (q = 0), sua energia potencial máxima é dada por ).
d) O movimento da partícula possui momento angular constante e perpendicular ao plano da folha.
e) Todas as alternativas acima estão corretas.
Ver solução completaQuestão 42
Num experimento de momento angular mostrado na foto ao lado, um anel é colocado em contato com uma mesa giratória, de tal maneira que o eixo do anel coincida com o eixo de rotação da mesa (colisão angular inelástica). Antes do contato com o anel, a mesa girava com velocidade angular decrescente por causa do atrito com os rolamentos. Durante o experimento, a velocidade angular variou conforme ilustrado no gráfico.
Assuma que:
- o anel possui o mesmo momento de inércia que o da mesa giratória em relaçao àquele eixo de rotação,
- a força de atrito entre os rolamentos e a mesa giratória é constante durante todo o movimento.
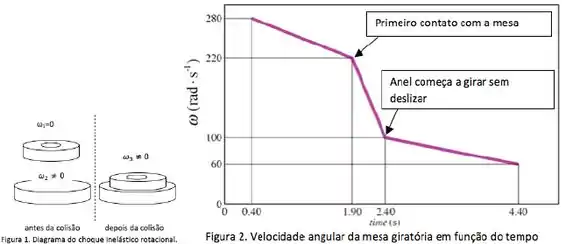
Expresse todas as suas respostas em função de e dos dados do gráfico.
a) Calcule o torque da força de atrito entre os rolamentos e a mesa giratória
b) Calcule a energia cinética total do sistema anel-mesa logo antes da colisão () e
logo depois que o anel e a mesa começam a girar com mesma velocidade angular ().
c) Calcule a energia dissipada pelo atrito entre a mesa e os rolamentos durante o intervalo
de tempo de 1,9 s a 2,4 s.
d)Calcule a energia dissipada pelo atrito entre a mesa e o anel durante o intervalo de
tempo de 1,9 s a 2,4 s.
Ver solução completaQuestão 43
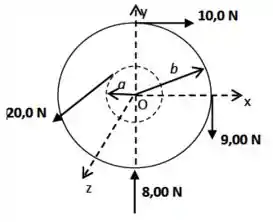
Sobre o disco de raio , situado no plano , são aplicadas as forças como mostra a figura. As forças de e tangenciam o disco, a força de é normal do disco e a força de tangencia o círculo de raio . Qual o torque resultante sobre o disco, em relação ao eixo que passa por e perpendicular ao disco. Considere e .
Ver solução completa
Questão 44
Um disco de raio e massa e um cubo de lado e mesma massa, estão no topo de um plano com comprimento inclinado de com a horizontal. Existe atrito entre o plano inclinado e os dois objetos, os coeficientes de atrito cinético e atrito estático são respectivamente e . Na base do plano existe um trilho na vertical com o formato de um anel de raio como ilustra o desenho. A base do plano e o trilho têm superfícies com atrito desprezível. Na saída do trilho, está em repouso um segundo cubo idêntico ao primeiro com seu centro de massa na posição . Logo após o segundo cubo, a superfície horizontal apresenta um coeficiente de atrito cinético variável e no final desta superfície está uma mola com constante elástica . A superfície embaixo da mola tem atrito desprezível. A origem do sistema de coordenadas coincide com o centro do anel. A aceleração da gravidade é . Desenvolva as equações na forma literal para somente no final substituir as variáveis pelos valores fornecidos.
c) Calcule o torque produzido no disco pela força da gravidade em relação ao ponto de contato com o plano inclinado.
Ver solução completaQuestão 45
Um disco de raio e massa e um cubo de lado e mesma massa, estão no topo de um plano com comprimento inclinado de com a horizontal. Existe atrito entre o plano inclinado e os dois objetos, os coeficientes de atrito cinético e atrito estático são respectivamente e . Na base do plano existe um trilho na vertical com o formato de um anel de raio como ilustra o desenho. A base do plano e o trilho têm superfícies com atrito desprezível. Na saída do trilho, está em repouso um segundo cubo idêntico ao primeiro com seu centro de massa na posição . Logo após o segundo cubo, a superfície horizontal apresenta um coeficiente de atrito cinético variável e no final desta superfície está uma mola com constante elástica . A superfície embaixo da mola tem atrito desprezível. A origem do sistema de coordenadas coincide com o centro do anel. A aceleração da gravidade é . Desenvolva as equações na forma literal para somente no final substituir as variáveis pelos valores fornecidos.
a) Os dois objetos são liberados a partir do repouso e descem o plano inclinado. O disco desce rolando sem deslizar. Utilize a 2ª Lei de Newton para determinar qual dos dois objetos chega primeiro à base do plano. Para este item um sistema de coordenadas diferente do proposto no desenho pode ser utilizado.
Ver solução completaQuestão 46
Na preparação para um salto com vara, o atleta ilustrado abaixo mantém a vara em equilíbrio estático na posição horizontal. Para isto ele faz numa extremidade da vara, posição A, uma força na vertical para baixo igual a e na posição B uma força na vertical para cima igual a . A vara tem comprimento igual a 5,0 𝑚 e massa 3,0 𝑘𝑔.
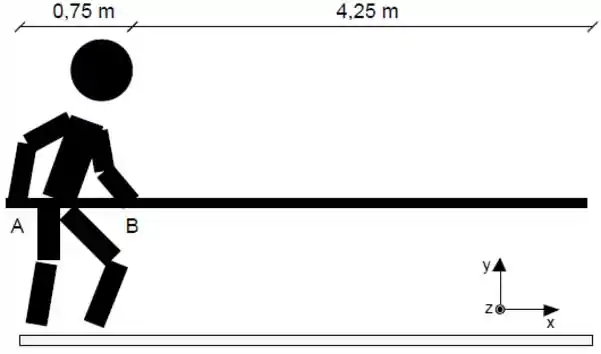
a) Calcule o momento de inércia rotacional da vara em relação ao eixo que passa pelo ponto B na direção do eixo .
b) Determine as forças e .
c) Suponha agora que em 𝑡 = 0 o atleta solte a vara na posição B e mantenha firme a posição A, de forma que a vara possa girar livremente em torno da posição A no plano em direção ao chão. Calcule o módulo da aceleração angular da barra neste instante.
d) Calcule a velocidade angular da barra quando o deslocamento angular for igual a .
Ver solução completaQuestão 47
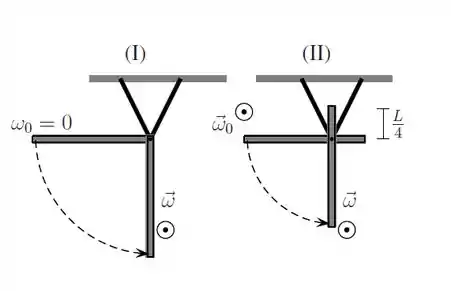
Seja um corpo rígido composto de uma esfera maciça de massa e raio , uma esfera oca de massa e raio , e uma barra fina de massa e comprimento . Este corpo está sobre uma mesa horizontal e pode girar em torno de um eix vertical fixo que passa no centro da barra, indicado pelo ponto na figura abaixo. Não há atrito com a mesa ou com o eixo de rotação.
Calcule o momento de inércia deste corpo em relação ao eixo indicado.
Sejam duas forças agindo no centro de cada esfera, como mostrado abaixo. Os módulos das forças aplicadas são e . Encontre o módulo da aceleração angular e o sentido da rotação resultante (horário ou anti-horário).
Agora, duas forças agem nas posições indicadas: a força a uma distância L/4 do centro da barra e a força no centro da esfera oca. Os módulos das forças aplicadas são e . Calcule o ângulo necessário para que o corpo não apresente movimento rotacional.
Ver solução completaQuestão 48
Um ioiô com massa e com raio do eixo possui momento de inércia de . Sua corda tem de comprimento, é inextensível e tem massa desprezível. No momento em que é lançado verticalmente para baixo, o ioiô tem somente velocidade de translação . Assuma que não há deslizamento entre a corda e o eixo do ioiô.
Escreva as equações de movimento do ioiô sob sua forma literal.
Determine o valor da aceleração do centro de massa do ioiô durante seu moviemento
Determine a energia cinética total do ioiô no instante em que ele chega 60 cm abaixo do ponto da onde foi lançado.
Determine o valor da energia cinética relacionada ao movimento de rotação neste instante.
Ver solução completaQuestão 49
Um disco fino e homogêneo de raio encontra-se em repouso sobre uma superfície horizontal sem atrito. Num dado instante aplicam-se na periferia do disco três forças tangenciais e uma radial, todas de mesma intensidade com direções, sentidos e pontos de aplicação conforme indicados na figura. Nesse instante, o módulo do torque resultante em relação ao centro do disco é
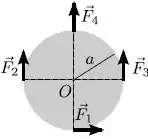
- ;
- ;
- ;
- ;
- ;
Questão 50
Uma chapa quadrada fina e homogênea de lado encontra-se sobre uma superfície horizontal sem atrito presa por um pino em um dos seus vértices. Num dado instante aplicam-se quatro forças horizontais e de mesma intensidade perpendiculares aos lados do quadrado como mostra a figura. O módulo do torque resultante em relação a é
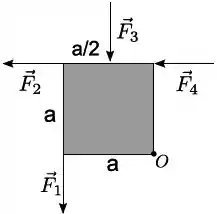
- ;
- ;
- ;
- ;
- ;
Questão 51
Uma pequena esfera de massa está presa a um fio ideal de comprimento , que tem a outra extremidade presa a um ponto no teto. A esfera está presa a uma mola ideal que se encontra na horizontal e tem sua outra extremidade presa na parede. No instante mostrado na figura, a mola se encontra comprimida em relação a seu comprimento natural e exerce sobre a esfera uma força de módulo .
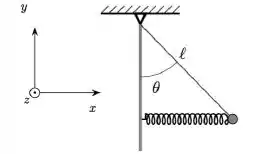
No sistema de eixos indicado na figura, qual o torque que a força elástica da mola exerce sobre a esfera em relação ao eixo paralelo a , que passa pelo ponto de sustentação do fio?
a) O torque é nulo
b)
c)
d)
e)
f)
g)
Ver solução completaQuestão 52
Calcule o momento angular de um sistema constituído de duas partículas, e , em relação ao ponto , no instante indicado na figura. As massas e as velocidades das partículas e , respectivamente , , e . Considere o eixo positivo para fora da prova.

Escolha uma:
Questão 53
Um sistema é composto por uma haste de massa e comprimento , que está livre para girar em torno de um eixo que passa pelo seu centro de massa, e por duas massas pontuais e , que se encontram afixadas nas extremidades da haste, conforme mostra a figura. Inicialmente, haste e massa estão em repouso na direção horizontal, quando são liberadas e passam a exercer rotações em torno do eixo no sentido horário. Despreze os efeitos e resistências do ar.
Determine as coordenadas e do centro de massa do sistema para a situação descrita.
Determine o momento de inércia de rotação associado ao sistema.
Determine o vetor torque em relação ao eixo de rotação exercido pela força peso de cada componente do sistema e o vetor torque resultante, indicando sua direção em termos dos vetores unitários de base, conforme indicado na figura.
Utilizando conceitos de energia e seu princípio da conservação, determine a velocidade angular de rotação do sistema ao passar pela posição vertical. Poderíamos também utilizar as expressões da cinemática rotacional para calcular a velocidade angular? Justifique.
Ver solução completaQuestão 54
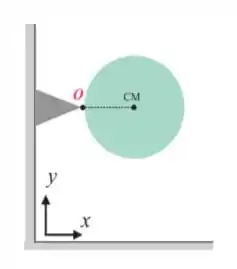
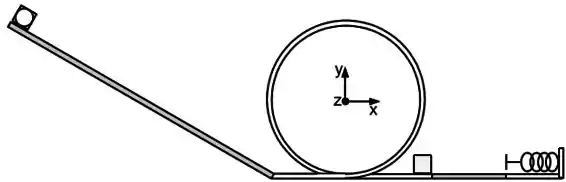
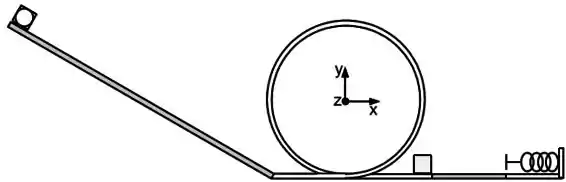
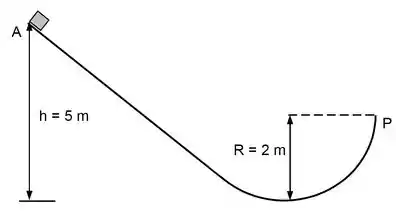
Um bloco de massa desconhecida é solto do repouso na posição em uma rampa sem atrito com formato de quarto de círculo ilustrado abaixo. Calcule a componente radial da aceleração e o módulo da aceleração angular do bloco quando ele atingir a posição P.
Utilize
nenhuma das respostas acima.
Ver solução completaQuestão 55
A figura mostra 4 diagramas de corpo livre de uma polia de peso W = 20 N. Em qual ou quais diagrama(s) a polia está em equilíbrio?
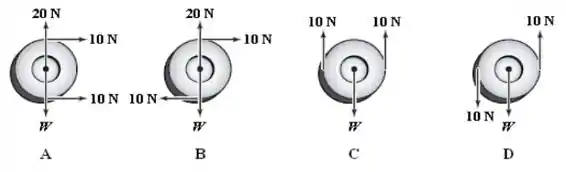
a) A
b) B
c) C
d) D
e) A e C
Ver solução completaQuestão 56
Uma bola de bilhar recebe uma tacada como indicada na figura. O atrito entra a bola e a mesa é desprezível. Imediatamente após a tacada, pode-se afirmar que:
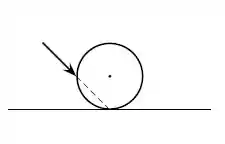
a) a bola se desloca para direita e gira no sentido anti-horário
b) a bola se desloca para esquerda e gira no sentido horário
c) a bola se desloca para direita e gira no sentido horário
d) a bola se desloca para esquerda e gira no sentido anti-horário
e) a bola se desloca para direita e não gira
Ver solução completaQuestão 57
Um pêndulo cônico é constituído por uma partícula presa a um fio ideal, de comprimento L, que faz um ângulo θ com a vertical, de modo que a partícula execute um movimento circular uniforme, com centro no ponto C, com velocidade angular ω como ilustra a figura. Sendo o módulo do torque da partícula em relação ao ponto C e a o módulo da aceleração da partícula respectivamente, podemos afirmar:
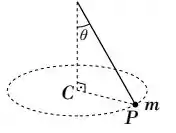
a)
b)
c)
d)
e)
f)
g)
Ver solução completaQuestão 58
Um disco homogêneo de massa M e raio R encontra-se sobre uma mesa horizontal completamente lisa, sem estar preso a ela. Em um dado instante duas forças estão aplicadas tangencialmente na beirada do disco, uma em um ponto diametralmente oposto ao ponto de aplição da outra. Sabendo que o momento de inércia do disco relativo ao eixo perpendicular a ele que passa pelo seu centro de massa é , e denotando por acm e α os módulos respectivos da aceleração do centro de massa do disco e da aceleração angular de rotação em torno do eixo no instante considerado, podemos dizer que:
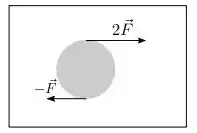
a)
b)
c)
d)
e)
f)
Ver solução completaQuestão 59
Temos dois discos sobre uma mesa, onde um fluxo de ar (na mesa) elimina ao trito no deslocamento horizontal. Um disco está preso pr uma corda a um pivô fixo. O outro disco vem com uma velocidade incial e colide com o primeiro. Após a colisão, os dois discos ficam colados. Sobre leis de conservação, podemos dizer que para o sitema (discos + corda):
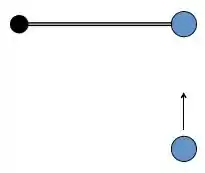

Questão 60
(Capítulo 9.1 – Exercício 61) Um pêndulo consistindo em um fio de comprimento preso a uma bolinha de massa oscila em um plano vertical. Quando o fio forma um ângulo com a vertical, (a) calcule a aceleração tangencial da bolinha, usando . (b) Qual é o torque exercido em relação ao ponto pivô? (c) Mostre que , com , fornece a mesma aceleração tangencial encontrada na parte (a).
Ver solução completaQuestão 61
Um bloco de inércia sobre uma rampa sem atrito está preso a um barbante fino. O barbante passa por uma polia e está preso a uma massa pendurada . A rampa está inclinada com um ângulo de acima da horizontal.
- Considerando a polia ideal e sem atrito, determine o valor de que faz o sistema se mover de forma que o bloco de inércia suba a rampa com velocidade constante.
- Considerando agora que a polia é um disco com inércia e raio , determine o valor de que faz o sistema se mover e forma que o bloco de inércia suba a rampa com aceleração .
Questão 62
Considere um anel de espessura desprezível, um cilindro sólido e uma esfera maciça, todos com mesma massa e raio , que são abandonados do alto de um plano inclinado e descem o plano, rolando sem deslizar. Sobre o tempo que eles demoram para atingir a base do plano, pode-se afirmar que:
a) A esfera atinge o plano primeiro, em segundo o cilindro e por último o anel
b) O cilindro e o anel chegam juntos, antes da esfera
c) Todos os objetos chegam ao mesmo tempo
d) O anel chega primeiro, em segundo o cilindro e por último a esfera
e) O cilindro e a esfera chegam juntos, antes do anel
Ver solução completaQuestão 63
Um disco possui momento de inércia de e está submetido a uma aceleração angular constante de . Se o disco partiu do repouso o trabalho realizado nos primeiros segundos pelo torque resultante foi de:
Questão 64
15. Um disco homogêneo de raio e massa está fixo por um pino a uma parede vertical no plano , conforme a figura abaixo. O disco pode girar, sem atrito, ao redor do eixo fixo que é perpendicular ao plano , e que passa pelo ponto O distante do centro do disco. O disco não encosta na parede e, portanto, não há atrito com a parede vertical. Inicialmente, o centro de massa está na altura do eixo de rotação e um pequeno pino impede o disco de girar. O módulo do vetor aceleração angular do disco no instante em que o pino é removido, em , é:
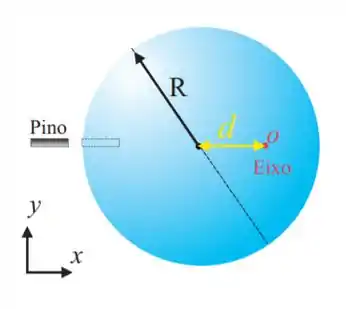

Questão 65
Q - Uma partícula de massa move-se em um plano horizontal . O vetor posição, que aponta da origem para a partícula, é dado por , com unidades no SI. Podemos afirmar que, no instante , o módulo do vetor torque em relação a origem , em , a que a partícula está sujeita é:
Ver solução completaQuestão 66
Q - Considere uma bola de massa fixa em uma semi-circunferência rígida de raio e de massa muito menor que a massa da bola. Inicialmente o dispositivo é abandonado de acordo com a figura, onde , e rola sem deslizar sobre a superfície horizontal.
Desenhe o diagrama de corpo livre do sistema bola semi-circunferência, e escreva as equações de movimento do sistema (não precisa resolvê-las).
Desenhe o diagrama de corpo livre estendido, e complemente as equações do item anterior com a equação para rotações (não precisa resolvê-las).
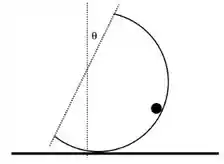
Questão 67
Uma chapa metálica quadrada de lado , homogênea e de massa encontra-se em repouso sobre um plano horizontal , sem atrito, com o seu centro de massa localizado na origem . Num dado instante aplicam-se as forças e em dois vértices da chapa como mostra a figura. A opção que corresponde ao torque resultante em relação ao ponto , imediatamente após as forças serem aplicadas é:
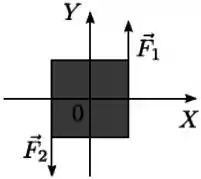
- ;
- ;
- ;
- ;
Questão 68
Considere um pêndulo constituído de uma massa que oscila, pendurada por um fio sem massa e de comprimento constante. A aceleração não se anula em nenhum dos pontos A, B ou C, mas a velocidade se anula nos pontos A e B.
Ver solução completaQuestão 69
Nas duas situações a seguir, as barras são idênticas, têm comprimento e estão sobre uma mesa de atrito desprezível. Enquanto na situação (a) a barra está presa por uma extremidade, em (b) ela está presa em seu centro. Além da força exercida pelo pino que prende a barra à mesa há uma força externa atuando em cada barra, nas posições indicadas na figura abaixo. Sobre o módulo do torque resultante e o módulo da aceleração angular em relação ao ponto fixo de cada barra, é correto afirmar que:
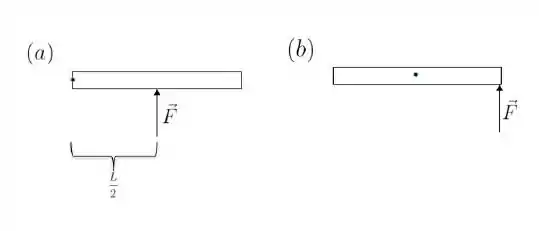
a) e
b) e
c) e
d) e
e) e
f) e
Ver solução completaQuestão 70
Considere duas barras finas, homogêneas, de comprimento e massa . Ambas têm um de seus pontos presos a um suporte no teto de maneira que podem girar, livremente, em torno desse ponto. Uma delas (I) está presa por uma de suas extremidades enquanto a outra (II) está presa a um ponto localizado a uma distância de uma de suas extremidades. Considere que a barra I é abandonada do repouso, quando se encontra na horizontal e a barra II é lançada, a partir da posição horizontal, com uma velocidade angular diferente de zero, de maneira que ambas chegam na posição vertical com mesma velocidade angular . Sobre a energia cinética e o módulo do torque resultante em relação ao ponto fixo de cada barra quando elas passam pela posição vertical, é correto afirmar que:
a) e
b) e
c) e
d) e
e) e
f) e
Ver solução completaQuestão 71
A figura mostra uma haste rígida de massa M e comprimento l, a qual pode girar em torno de um eixo horizontal que passa pelo seu centro de massa (mostrado como ponto O na figura). Há uma força de atrito entre o eixo de rotação e a haste. Uma bolinha de massa m e raio desprezível é conectada a uma extremidade da haste. Inicialmente o sistema está na posição vertical conforme mostra a figura; ele começa a rodar no sentido horário sob efeito da gravidade, até parar numa posição na qual o ângulo de rotação com relação à direção original é de .
- Calcule o trabalho da força de atrito durante o movimento.
- Supondo constante o módulo do torque da força de atrito durante o movimento, qual o seu valor?
- Qual a aceleração angular (módulo, direção e sentido) do sistema em função do ângulo que a haste faz com a horizontal.
Dados:
Para a barra:
Questão 72
Dentre as afirmações abaixo, quais dentre elas são falsas?
I. Se dois vetores possuem direções exatamente opostas entre si, o produto vetorial entre eles é nulo.
II. A magnitude do produto vetorial entre dois vetores é mínima quando os vetores são perpendiculares.
III. Conhecendo-se a magnitude do produto vetorial entre dois vetores não nulos e as magnitudes de cada vetor individualmente, o ângulo entre eles é determinado univocamente.
(A) I e III
(B) I, II e III
(C) III
(D) II e III
(E) Nenhuma delas é falsa.
Ver solução completaQuestão 73
Dois discos de mesmo raio e de massa diferentes, onde , estão presos ao teto por fios ideais e enrolados em suas bordas. Liberados a partir do repouso eles caem verticalmente onde é o módulo da aceleração local da gravidade; o momento de inércia de um disco em torno do seu eixo de rotação que passa pelo seu centro é igual . Os módulos das trações nos fios em cada disco são e e as acelerações dos seus centros de massa são e , respectivamente, a opção correta abaixo é:
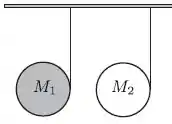
- ;
- e
Questão 74
Um fio ideal se encontra enrolado em torno de um cilindro maciço de massa e raio e não desliza sobre o cilindro. O cilindro gira com atrito desprezível em torno de um eixo horizontal fixo, sendo seu momento de inércia em relação a esse eixo. O fio passa por uma polia de massa desprezível. A outra extremidade do fio está amarrada a uma bola de borracha de massa , de raio desprezível, que se encontra inicialmente em repouso a uma altura do solo, como mostra a figura.
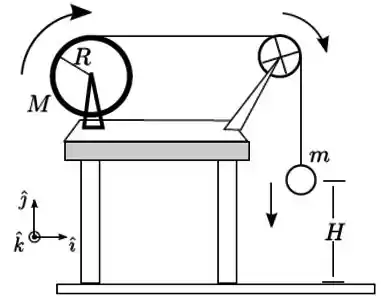
Considere que: os fios são ideais; os fios permanecem esticados durante todo o tempo; a resistência do ar é desprezível; a gravidade tem módulo conhecido.
Supondo que o fio se encontre inicialmente esticado e a bola colida elasticamente com o solo, determine:
a) o módulo da velocidade com que a bola colide com o solo;
b) o módulo da tensão no fio no instante imediatamente anterior à colisão da bola;
Ver solução completaQuestão 75
Um carretel é composto por um cilindro interno de raio e massa , enrolado por um fio ideal, com 2 discos idênticos, de massa e raio cada um, por fora do cilindro interno, concêntricos a este último (como um iô-iô). Inicialmente o carretel está em repouso em uma superfície horizontal quando o fio enrolado ao cilindro interno começa a ser puxado na direção horizontal, conforme a figura, por uma força de módulo . Observa-se que o cilindro rola sem
deslizar sobre a superfície horizontal e sabe-se que o momento de inércia de um cilindro de massa m e raio r′ em relação a um eixo que passa por seu eixo desimetria é .
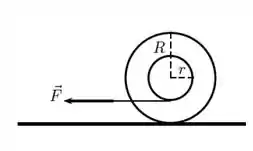
Indique as respostas em termos de .
(a) Mostre que o momento de inércia do carretel, em relação a seu eixo de simetria, vale
(b) Qual a direção e o sentido da força de atrito que atua no carretel?
(c) Determine o módulo e o sentido da aceleração do centro de massa do carretel.
(d) Qual a velocidade angular de rotação do carretel, em torno do eixo de simetria
que passa por seu centro de massa, após ele completar uma volta depois do instante
em que a força começa a atuar?
(e) Determine a energia cinética associada ao carretel no instante em que ele completa
a primeira volta após o início da aplicação da força .
Ver solução completaQuestão 76
Um mergulhador de está na extremidade direita de uma prancha de massa desprezível de de comprimento. A prancha é sustentada por dois pilares que distam entre si, conforme a figura. Encontre a magnitude e a direção da força exercida pelo pilar sobre a prancha.
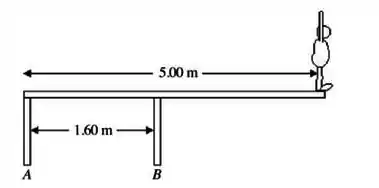
(A) , vertical para baixo.
(B) , vertical para cima.
(C) , vertical para baixo.
(D) , vertical para cima.
(E) zero.
Ver solução completaQuestão 77
Uma barra de massa e comprimento roda livremente em um eixo localizado em uma de suas laterais. A barra é solta da posição horizontal. Qual a aceleração angular quando a barra faz um ângulo de 30º com a vertical. Considere que o momento de inércia de uma barra em torno do centro de massa é .
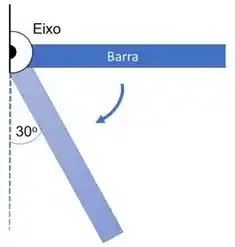
a)
b)
c)
d)
e)
Ver solução completaQuestão 78
3. Em um motor elétrico típico, a curva de torque é aproximadamente constante na faixa de rotações de trabalho do motor. Suponha que o eixo deste motor está conectado à uma roda de massa , em formato de cilindro. Sabendo que o torque do motor é dado por , obtenha a aceleração angular e a velocidade angular em função do tempo .
Questão 79
Um quadrado homogêneo de madeira de comprimento de lado é colocado sobre uma mesa horizontal e está livre para girar em torno de seu eixo central. O quadrado está sujeito a duas forças como mostrado na figura. Qual a magnitude do torque resultante sobre o quadrado em relação ao eixo de rotação?
(Obs.: Alteramos as opções, já que esta questão foi anulada.).
Ver solução completaQuestão 80
Considere um pêndulo cônico formado por um fio ideal de comprimento e uma pequena esfera de massa que descreve um movimento circular uniforme de raio e velocidade angular , conforme a figura a seguir.
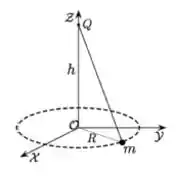
Sabemos que as quantidades relacionadas à rotação podem depender do ponto em relação ao qual são calculadas. Comparando sempre as quantidades em relação ao ponto O (centro do movimento circular) e Q (ponto onde o fio está fixo) qual a única das quantidades a seguir é a mesma?
(a) Torque causado pela força peso na esfera.
(b) Torque causado pela tração do fio na esfera.
(c) Torque causado pela força resultante na esfera.
(d) Momento angular da esfera.
Ver solução completaQuestão 81
Dois discos A e B de mesmo raio estão sobre uma mesa horizontal e plana e fixados por pinos nos seus centros, em torno dos quais podem girar livremente. Ambos os discos tem sua massa distribuída de maneira uniforme na sua área, mas o disco A tem massa maior que o disco B. Num dado instante começa a atuar sobre ambos, que inicialmente estavam em repouso, uma mesma força na periferia de cada um, como mostra a figura. Para os módulos dos torques resultantes e e das respectivas acelerações angulares e tem-se que:
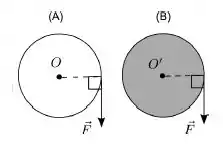
(a) ;
(b) ;
(c) ;
(d) ;
(e) ;
(f) ;
(g) ;
Ver solução completaQuestão 82
Considere agora um disco horizontal de raio com quatro hastes conforme a figura ao lado. NÃO é o carrossel do item anterior. Duas pessoas empurram esse disco no sentido anti-horário. Veja a figura abaixo com vista de cima. A força de cada pessoa tem módulo constante , sendo tangente à borda. Não há atrito entre o eixo central e o disco. O sistema disco-hastes tem momento de inércia .
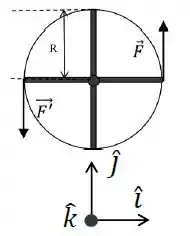
(b) Calcule a aceleração angular do sistema disco-hastes.
Ver solução completaQuestão 83
Uma pequena esfera ligada a uma haste rígida leve gira em torno de um eixo perpendicular que está fixado à outra extremidade da haste. Em um certo sistema de referências, a sua velocidade angular é negativa, e a sua aceleração angular é positiva. Se um observador neste sistema de referências se posicionar de modo a ter o eixo de rotação apontando diretamente para si, ele observará a esfera:
- Girando no sentido horário e desacelerando.
- Girando no sentido anti-horário e desacelerando.
- Girando no sentido horário e acelerando.
- Girando no sentido anti-horário e acelerando.
- Primeiro girando no sentido anti-horário e, em seguida, no sentido horário.
Questão 84
Considere um haltere formado por duas pequenas esferas de massa , presas por uma barra de comprimento e massa desprezível. O sistema repousa em uma mesa horizontal sem atrito quando começam a atuar, simultaneamente, duas forças e de mesmo módulo conhecido . A força atua em uma das esferas, na direção da barra e a força atua na outra esfera, em uma direção perpendicular a , conforme mostra a figura.
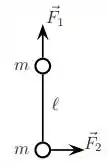
Pode-se afirmar que no instante em que as forças começam a atuar:
(a) O módulo do torque resultante em relação à posição do centro de massa da barra é .
(b) O módulo do torque resultante em relação à posição do centro de massa da barra é .
(c) O módulo do torque resultante em relação à posição do centro de massa da barra é .
(d) A aceleração angular do haltere em torno do centro de massa se relaciona com a aceleração do centro de massa por .
(e) A aceleração angular do haltere em torno do centro de massa se relaciona com a aceleração do centro de massa por .
(f) A aceleração do centro de massa é nula.
(g) A aceleração angular em torno da posição do centro de massa do sistema é nula.
Ver solução completaQuestão 85
Uma haste longa e fina de massa e comprimento é livre para girar sobre um ponto localizado a de seu comprimento. A haste é posicionada na posição horizontal, como mostrado na figura , por um fio preso na extremidade:
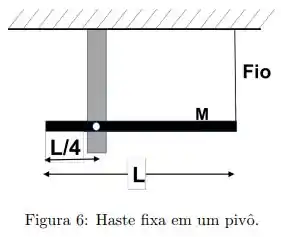
Em um dado momento o fio é cortado e a haste fica livre para girar em torno do eixo.
Dados: Momento de inércia em relaç��o ao eixo de rotação perpendicular a haste e passando pelo pivô é
(c) Calcule a aceleração angular da haste no momento que o fio é cortado.
Ver solução completaQuestão 86
Duas massas, uma com massa e outra com massa , estão presas a uma haste rígida horizontal muito leve, como mostrado na Figura 4. Quando o sistema é liberado a partir do repouso, a haste começa a girar em torno de um eixo perpendicular à página com uma aceleração angular de:
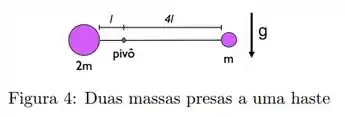
A.
B.
C.
D.
E.
Ver solução completaQuestão 87
Um parafuso deve ser apertado com um torque de no sentido horário, aplicando-se uma das forças mostradas na chave da figura. As intensidades das forças são e . Qual das forças abaixo produz o torque necessário?
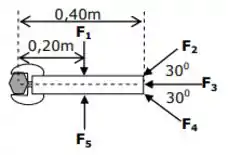
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 88
Duas rodas, uma de raio R e outra de raio 2R, são fixadas uma sobre à outra de modo concêntrico e sãolivres para rodar em torno de seu eixo de simetria. Como mostrado abaixo, quatro forças são exercidastangencialmente às rodas.
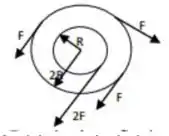
Qual é a magnitude do torque resultante?
- Zero
Questão 89
Um ioiô é pendurado ao teto por um fio que não possui massa nem atrito. Ele é liberado verticalmente a partir do repouso como mostra a figura. O seu centro de massa cai de uma altura em relação a sua altura inicial e, durante a queda, o seu centro de massa move-se verticalmente. A afirmativa correta sobre a dinâmica do ioiô durante a queda é
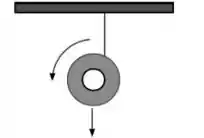
- Tração do fio varia linearmente com o tempo durante a sua queda.
- Em relação ao centro de massa do ioiô o torque resultante é nulo.
- Em relação ao centro de massa do ioiô o torque da tração é nulo.
- O torque resultante devido às forças peso e tração sobre o ioiô é constante.
- a força peso não realiza trabalho sobre o ioiô.
Questão 90
As duas questões abaixo relacionam-se à figura:
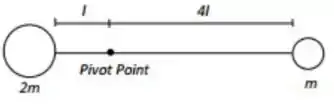
2. Um sistema é formado por dois corpos, um com massa m e o outro com massa 2m, que estão ligados por uma haste rígida sem massa de comprimento 5l. Como mostrado na figura acima, o sistema pode girar ao redor de um eixo horizontal que atravessa o “Pivot Point”. O sistema está sob a ação da aceleração da gravidade g. Quando o sistema é liberado, a haste começa a rodar com uma aceleração angular cuja magnitude é:
a)
b)
c)
d)
e)
3. Em que momento a aceleração angular se anula?
a) Nunca.
b)Quando o sistema se encontra na vertical.
c) Quando o sistema encontra-se na horizontal, com as posições das massas invertidas.
d) No momento que o torque é máximo.
e) Nenhuma das anteriores.
Ver solução completaQuestão 91

A lança ilustrada abaixo tem comprimento e massa . Considere a massa uniformemente distribuída. Ela estaria livre para girar, sem atritos, em torno do seu eixo localizado na extremidade inferior (A), contudo, duas forças a mantém em equilíbrio estático fazendo um ângulo com a horizontal. Uma delas tem módulo , está inclinada de em relação à horizontal e atua no centro de massa da lança (B). A outra força tem módulo e atua verticalmente para baixo na extremidade superior da lança (C). Utilize para a aceleração da gravidade.
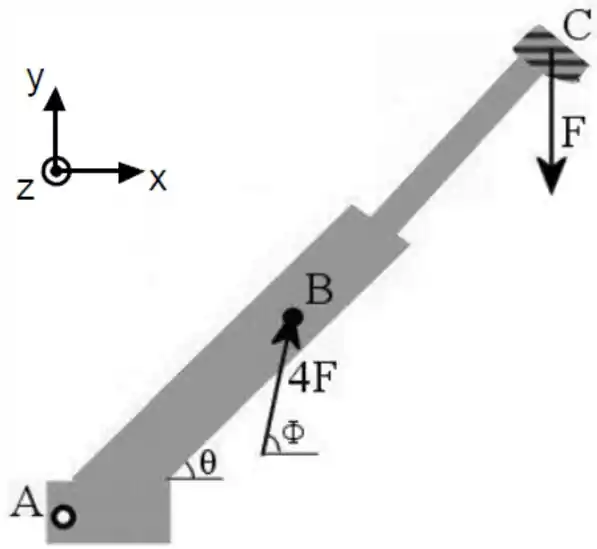
a) Determine os vetores torque em torno de A, produzidos na lança por cada uma das forças e .
b) Suponha agora que as forças e parem de atuar e a lança começa a girar pela ação da força da gravidade. Determine o valor da aceleração angular quando ela passar pela posição horizontal.
c) Continuando seu movimento de rotação, a lança passa pela posição vertical. Determine o valor da velocidade angular nesta posição.
Ver solução completaQuestão 92
No disco de e de raio são aplicadas as forças como indicadas na figura. O disco pode girar e torno do eixo que passa pelo ponto e é perpendicular ao disco.
Dados: ; ;
- Calcule o torque resultante em relação ao eixo de rotação que passa em .
- Calcule o momento de inércia do disco em relação ao eixo de rotação que passa em .
- Calcule a aceletação angular do disco e a aceleração tangencial no ponto onde a força atua.
Questão 93
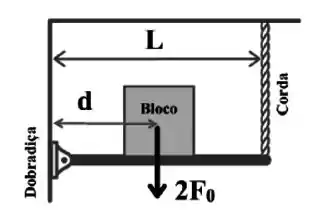
Uma barra uniforme de comprimento e de massa desprezível é suspensa horizontalmente por uma dobradiça e uma corda, conforme a figura abaixo. Um bloco de peso é colocado sobre a barra de forma que a dobradiça fique a uma distância do seu centro, como mostrado na figura. Se a tensão da corda não pode exceder , quais são o máximo valor de e o módulo da força sobre a dobradiça nesta situação?
Questão 94
No espaço sideral, longe da influência gravitacional de qualquer planeta ou estrela, dois veículos espaciais munidos de fogutes estão acoplados a uma estação espacial longa de de comprimento. O sistema todo encontra-se em repouso. A massa de um dos veículos é e a do outro . A massa da estação espacial é e esta pode ser considerada como um cilindro delgado homogêneo. Os foguetes são acionados simultaneamente, de forma que a magnitude da força de reação dos gases de exaustão sobre cada veículos (i.e., o empuxo) é de e pode ser considerada perpendicular à estação espacial.
Importante: Quando necessário, faça substituições numéricas apenas nas expressões analíticas finais. Quantidades vetoriais devem ser expressas num sistema de coordenadas com uma base apropriada de versores.
Dados: (barra)
(a) Calcule a posição do centro de massa CM do sistema “veículos + estação espacial” com respeito à posição do centro de massa da estação espacial. Trate os veículos como massas pontuais.
(b) Escreva a equação de movimento para o CM do sistema do ítem (a) num referencial inercial antes e depois do acionamento dos foguetes. Que movimento descreve o CM após o acionamento?
(c) Determine o momento de inércia do sistema do ítem (a) com respeito a um eixo passando pelo seu CM e perpendicular ao plano de movimento dos veículos após o acionamento dos foguetes.
(d) Determine o vetor torque total com respeito ao CM devido ao empuxo dos foguetes.
(e) Calcule a magnitude da velocidade angular de rotação do sistema após o acionamento dos motores.
Ver solução completaQuestão 95
O objeto ilustrado na figura ao lado pode girar livre em torno do eixo fixo . Ele é composto 6 por hastes finas. As 2 hastes ao longo dos eixos e têm, cada uma, comprimento e massa e estão presas pelo seu seu centro de massa ao eixo de rotação. As 4 hastes inclinadas têm, cada uma, a mesma massa . Em determinado instante , a força de módulo na direção horizontal é aplicada no ponto conforme mostra a figura. No mesmo instante, outra força de módulo e com a inclinação igual a inclinação da haste é aplicada no ponto .
a) Mostre que o momento de inércia do objeto em torno do eixo é dado por .
b) Escreva os vetores e necessários para calcular o torque em torno do eixo provocado pela força aplicada em , em . Calcule o produto vetorial e encontre .
c) Calcule o torque em torno do eixo provocado pela força aplicada em , em .
d) Calcule a aceleração angular do objeto neste instante.
e) Suponha agora que, para impedir o objeto de girar, uma terceira força é aplicada na direção horizontal no ponto , em . Determine esta forca .
f) Se ao invés da força aplicada no item anterior, a força em B for . Calcule a força que o eixo faz no objeto para que este fique em equilíbrio estático.
Ver solução completaQuestão 96
O ordenamento correto das magnitudes das acelerações angulares a das massas pontuais em trajetórias circulares é:
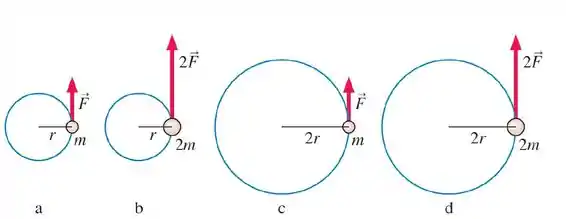
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 97
Uma barra delgada homogênea de massa e comprimento encontra-se suspensa horizontalmente com a extremidade apoiada na borda de uma mesa e a outra extremidade suspensa por um fio inextensível e de massa desprezível preso ao teto. O fio é cortado com uma tesoura e o instante imediatamente após o corte será chamado de .
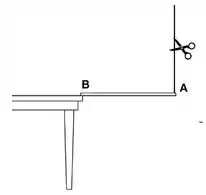
(a) Adote um sistema de coordenadas, esboce o diagramas de forças sobre a barra antes e imediatamente após o corte do fio. Escreva todas as forças explicitamente nas duas situações acima em termos da base de versores adotada.
(b) Antes do corte do fio, ou seja, para , determine a magnitude das forças e .
(c) Determine o vetor torque com respeito ao ponto no instante .
(d) Determine o vetor aceleração angular da barra em ao girar em torno de um eixo passando por .
(e) Determine o vetor aceleração do centro de massa em .
(f) Determine a força de reação da mesa sobre a extremidade da barra em . Qual a razão entre a magnitude dessa força em e em ?
IMPORTANTE: Deixe todas as suas respostas em termos apenas das variáveis fornecidas no enunciado, da aceleração gravitacional local () e dos versores da base adotada.
Ver solução completaQuestão 99
Um limpador de janelas tenta apoiar uma escada em uma parede sem atrito e descobre que a escada desliza sobre o chão quando é apoiada com um ângulo menor do que com a horizontal, mas permanece no lugar quando o ângulo é maior do que Considerar O coeficiente de atrito estático entre a escada e o chão:
- depende do comprimento da escada;
- é aproximadamente 1,3;
- é aproximadamente 0,27;
- é aproximadamente 0,13;
- depende da massa da escada;
Questão 100
Um disco de raio e massa gira livremente com velocidade angular em torno de um eixo vertical que passa pelo seu centro de massa. Pela ação de um torque, o eixo de rotação é alterado para a horizontal em um intervalo de tempo , conforme a figura abaixo. Sabendo que o módulo da velocidade angular do disco manteve-se constante durante a aplicação do torque, mostre que o módulo do torque médio aplicado é dado por:
Questão 101
Uma barra é constituída de dois materiais homogêneos, aço (parte clara da barra na figura) com massa 2M e madeira (parte escura da barra) com massa M, distribuídos em cada metade da barra. Ela repousa sobre uma mesa horizontal e sem atrito. Aplica-se a mesma força , perpendicularmente ao extremo da barra nas situações (A) e (B) como indica a figura, fazendo-a girar em torno de um pino de articulação na situação (A) e na situação (B). As relações entre os módulos dos torques , em relação a , devido à força e os módulos das acelerações angulares resultantes α, nas situações (A) e (B), são dadas:
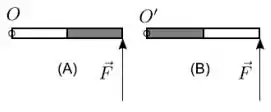
- e .
- e .
- e.
- e .
- e .
- Nenhuma das alternativas.
Questão 102
Um disco homogêneo gira ao redor de um eixo de rotação que passa no seu centro e é perpendicular à sua superfície. O seu momento de inércia em relação ao eixo de rotação é . A posição angular (em ) de um ponto no disco é dada por , onde o tempo é dado em segundos. O torque resultante no disco em relação ao seu centro no instante vale:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 103
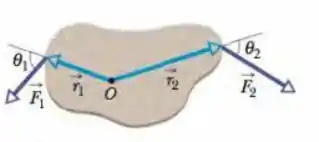
O corpo da figura abaixo, pode girar em torno de um eixo perpendicular ao papel passando por O e está submetido a duas forças, como mostra a figura. Se e, qual é o torque resultante em relação ao eixo?
Questão 104
Complete a seguinte afirmação: Quando um torque resultante é aplicado a um objeto rígido, ele sempre produz:
- Uma aceleração constante.
- Um equilíbrio rotacional.
- Uma velocidade angular constante.
- Um momento angular constante.
- Uma variação na velocidade angular.
Questão 105
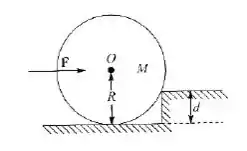
Calcule a magnitude da força horizontal que é preciso aplicar, em direção ao eixo , para conseguir que um tambor cilíndrico, de massa e raio , suba um degrau de altura
Questão 106
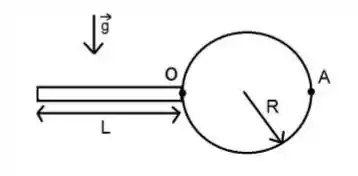
Um corpo formado por uma barra homogênea, de massa e comprimento , e por um disco, de massa e raio , pode girar em torno de um eixo que passa pelo ponto (na junção da barra e do disco) e é perpendicular ao plano da página. O corpo é mantido em repouso na horizontal, como vemos na figura. Considere .
(a) Calcule o momento de inércia da barra em relação ao eixo que passa pelo ponto . Dado: .
(b) Calcule o momento de inércia do disco em relação ao eixo que passa pelo ponto . Dado: .
(c) Calcule o módulo do torque resultante que age sobre o corpo no momento em que o corpo é solto.
(d) Calcule o módulo da aceleração adquirida pelo ponto (extremidade direita do disco) no momento em que o corpo é solto. Indique também a direção e sentido dessa aceleração.
Questão 107
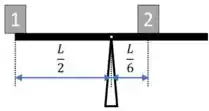
Questão 1) Dois blocos pequenos de massas iguais, , estão fixos em uma gangorra sem atrito, de massa desprezível e de comprimento , distantes de e do eixo de rotação. Inicialmente a gangorra encontra-se na horizontal, em repouso. Calcule o módulo da aceleração tangencial do bloco imediatamente após a gangorra ser liberada. Forneça sua resposta apenas em termos da aceleração da gravidade g.
Questão 108
Considere dois cilindros homogêneos, de mesma massa, porém um possui o dobro do raio do outro, conforme as figuras. Ambos os cilindros são livres para rodar em torno de um eixo que passa pelos seus respectivos centros e uma força tangencial é aplicada no topo de ambos, fazendo com que passem a girar. Para que ambos girem com a mesma aceleração angular, é preciso que:
(Dado: Se é a massa e é o raio de um cilindro homogêneo, )
(A) A força aplicada no cilindro menor tem de ser o dobro da força aplicada no cilindro maior.
(B) A força aplicada no cilindro menor tem de ser a metade da força aplicada no cilindro maior.
(C) A força aplicada no cilindro menor tem de ser a igual à força aplicada no cilindro maior.
(D) A força aplicada no cilindro menor tem de ser 4 vezes maior que a força aplicada no cilindro maior.
(E) A força aplicada no cilindro menor tem de ser 4 vezes menor que a força aplicada no cilindro maior
Ver solução completaQuestão 109
Uma força atuando sobre uma peça de uma máquina é dada pela expressão . O vetor da origem ao ponto onde a força é aplicada é dado por .
a) Faça um diagrama mostrando , , e o sentido do torque.
Ver solução completaQuestão 110
Um operário está usando uma chave de boca para afrouxar uma porca. A ferramenta tem de comprimento, e ele exerce uma força de sobre a extremidade do cabo formado um ângulo de com o cabo.
Qual torque o operário exerce sobre o centro da porca?
Ver solução completaQuestão 111
Três massas, , e estão afixadas em uma barra de massa desprezível que gira em torno do eixo com velocidade angular , conforme a figura.
Considere os vetores unitários conforme a figura. Para desacelerar o conjunto de massas , e é necessário realizar um torque na direção
Questão 112
Um ciclista, em uma bicicleta em movimento, aciona o freio traseiro. Assinale a alternativa incorreta:
a) O torque gerado pela força de atrito no pneu traseiro aponta na direção do momento angular do pneu.
b) A força de atrito entre o pneu traseiro e o chão aponta na direção contrária à do movimento.
c) O torque gerado pelo freio é maior, em magnitude, que o torque gerado pela força de atrito entre o pneu e o chão.
d) O torque gerado pelo freio aponta na direção do momento angular do pneu.
e) nenhuma das anteriores.
Ver solução completaQuestão 113
Uma roda de massa e raio rola sem deslizar sobre uma superfície horizontal com
atrito ao ser puxada por uma força , aplicada sobreo seu eixo. O coeficiente de atrito entre a roda e a superfície é , e a velocidade do centro de massa é . O momento de inércia total da roda éem torno do eixo que passa pelo seu centro de massa.
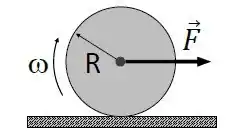
Considere que e . O maior valor do módulo da aceleração angular para o qual a roda não desliza é:
(A)
(B)
(C)
(D)
(E)
(F)
(G)
(H)
Ver solução completaQuestão 114
O objeto (sem massa) mostrado na figura está em equilíbrio? Explique.
Questão 115
Uma haste de massa e comprimento , pode girar em torno de um eixo que passa por uma de suas extremidades. Na outra extremidade está presa uma massa pontual de valor .
Inicialmente, haste e massa giram em um plano horizontal com velocidade angular no sentido horário. No instante t = 0 são exercidas duas forças como ilustradas abaixo. A força de módulo está aplicada no centro de massa da haste e tem direção perpendicular a ela. A força de módulo está aplicada na extremidade da haste e faz um ângulo de com ela. Despreze todos os atritos.

Calcule o vetor torque resultante no sistema em relação ao eixo.
Calcule o módulo da aceleração angular do sistema.
Calcule o trabalho realizado pelas forças até que o sistema pare de girar momentaneamente.
Suponha agora que seja zero e que a força de módulo não se altere. Calcule o
novo ângulo entre a haste e a outra força de módulo para que o sistema fique em
equilíbrio estático.
Ver solução completaQuestão 116
Seja uma barra de comprimento sobre a qual agem as forças ilustradas acima e sejam as seguintes equações:
Diga quais são as equações para a situação de equilíbrio estático, tomando como origem dos torques a extremidade superior da barra.
e
e
e
e
nenhuma das respostas acima.
Ver solução completaQuestão 117
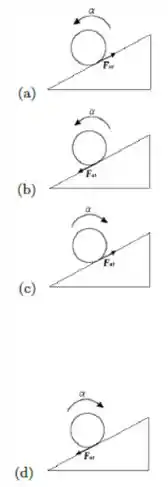
Um tambor cilíndrico rola sem deslizar sobre um plano inclinado. Além da força peso, apenas a superfície exerce força sobre o tambor. Em um determinado instante o tambor sobe o plano inclinado, com velocidade do centro de massa , conforme indicado na figura. Assinale a alternativa que melhor representa o sentido da força de atrito () no ponto de contato entre o plano e o tambor e o sentido da aceleração angula do tambor ()
Questão 118
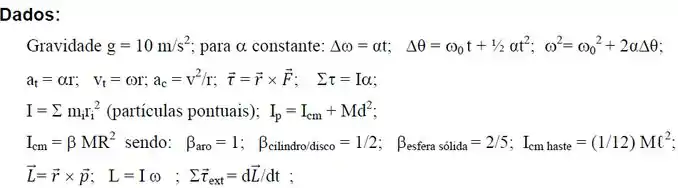
No instante de tempo um objeto esférico de massa e raio , gira deslizando com velocidade angular e velocidade do centro de massa nula em uma superfície horizontal com coeficiente de atrito cinético (veja a figura). Considere como ponto de contato do objeto com a superfície a origem do sistema de coordenadas. Utilize para a aceleração da gravidade.
a) Faça um diagrama de corpo livre do objeto.
b) Escreva as equações de Newton que descrevem o movimento.
c) Determine, enquanto o objeto rola deslizando, aceleração do seu centro de massa e sua aceleração angular .
d) Escreva as expressões em função do tempo para a velocidade do centro de massa e para a velocidade angular 𝜔(𝑡) do objeto enquanto ele rola deslizando.
e) Sabendo que no tempo o objeto esférico passa a rolar sem deslizar, ache a razão entre suas energias cinéticas de translação e rotação.
Ver solução completaQuestão 119
Duas cordas, com uma de suas extremidades presa ao teto, estão enroladas ao redor de um cilindro sólido de massa raio e comprimento . O cilindro é solto a partir do repouso.
- Com que aceleração o centro de massa do cilindro cai?
- Determine a tração em cada um dos fios.
- Quando o cilindro cai de uma altura , a partir do repouso, qual é a velocidade do seu centro de massa ?
Dado: O momento de inércia de um cilindro de massa e raio em relação a um eixo que passa pelo seu centro de massa é

Questão 120
Uma viga metálica de 400 kg e 4 m de comprimento estende-se horizontalmente, perpendicular à parede onde está presa. Um trabalhador de massa 70 kg está sentado na extremidade livre da viga. Qual o torque total sobre a viga em torno do ponto onde ela está presa na parede?
Ver solução completaQuestão 121
Que torque tem que ser exercido pelo pino na figura para evitar que o sistema gire?
Questão 122
A figura é um gráfico da posição angular (rad) do disco em rotação, no sentido indicado.
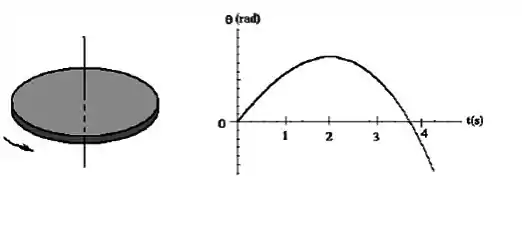
a) A velocidade angular do disco é positiva, negativa ou nula em t=0 s, t=1 s, t=2 s e t=3s.
b) A mesma pergunta do item a) para aceleração angular.
c) Indique na figura os vetores e nos instantes especificados.
Ver solução completaQuestão 123
Um haltere é constituído de uma barra rígida ligada por duas esferas de massas e , onde . Ele é deixado cair livremente a partir do repouso inclinado de em relação a horizontal como mostrado na figura. A descrição correta da queda do haltere é
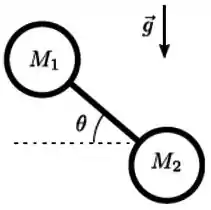
(a) ele cai mantendo a sua inclinação original sem girar.
(b) ele gira no sentido anti-horário e passa a cair alinhado horizontalmente.
(c) ele cai girando no sentido anti-horário pois .
(d) ele cai oscilando entre as inclinações e
(e) nenhuma das outras alternativas é correta.
Ver solução completaQuestão 124
. Um ioiô consiste em um objeto com simetria cilíndrica e um barbante enrolado em torno de um eixo central. O ioiô tem momento de inércia e raio do eixo central , e é solto do repouso mantendo a extremidade do barbante em uma posição fixa, descendo verticalmente. É correto afirmar que:
quanto maior o valor de , maior a aceleração angular do ioiô.
A energia potencial gravitacional se converte integralmente em energia cinética de rotação do ioiô.
A aceleração do ioiô é igual a , onde é a aceleração da gravidade.
o torque externo no ioiô é numericamente igual à tração no fio multiplicado pelo raio .
a aceleração angular do ioiô é numericamente igual a , onde é a aceleração da
gravidade.
Ver solução completaQuestão 125
Uma partícula massiva encontra-se grudada em uma das extremidades de uma barra sem massa (ver Figura abaixo). A outra extremidade da barra está conectada na origem do plano horizontal . A partícula e a barra giram no plano , de modo que a partícula descreve uma circunferência com centro no ponto . A posição angular da partícula (em rad) é dada por:
onde o tempo é dado em segundos. O momento de inércia da partícula em relação ao eixo perpendicular ao plano e que passa no ponto é .
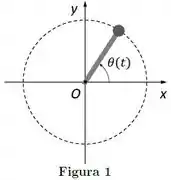
O módulo do torque resultante sobre a partícula em relação ao ponto no instante vale:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 126
O torque que faz uma força atuando no ponto será:
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 127
(Capítulo 9.1 – Exercício 61) Um pêndulo consistindo em um fio de comprimento preso a uma bolinha de massa oscila em um plano vertical. Quando o fio forma um ângulo com a vertical, (a) calcule a aceleração tangencial da bolinha, usando . (b) Qual é o torque exercido em relação ao ponto pivô? (c) Mostre que , com , fornece a mesma aceleração tangencial encontrada na parte (a).
Ver solução completaQuestão 128
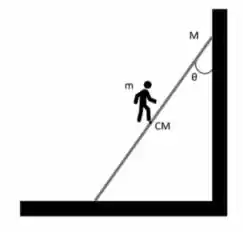
Um homem de massa sobe uma escada de massa que está no solo com coeficiente de atrito igual a , e também está apoiada na parede sem atrito formando um ângulo com a parede. Qual deve ser o ângulo limite para que o homem possa subir até o centro de massa da escada sem que ela deslize?
Questão 129
Empilham-se blocos idênticos, de comprimento cada um, sobre uma mesa horizontal. Qual é a distância máxima entre as extremidades do ultimo e do primeiro bloco para que a pilha não desabe? Sugestão: Considere as condições de equilíbrio, sucessivamente, de cima para baixo. Faça a experiencia! (use blocos de madeira, livro, tijolos, dominós, ... idênticos).
Ver solução completaQuestão 130
(Cap 9 – Ex 59) Um cilindro de , cujo raio é de , inicialmente em repouso, pode girar livremente em torno de seu eixo. Uma corda de massa desprezível é enrolada em torno dele e puxada com uma força de . Supondo que a corda não escorregue, determine (a) o torque exercido pela corda sobre o cilindro, (b) a aceleração angular do cilindro e (c) a rapidez angular do cilindro após .
Ver solução completaQuestão 131
(Cap 9 – Ex 59) Um cilindro de , cujo raio é de , inicialmente em repouso, pode girar livremente em torno de seu eixo. Uma corda de massa desprezível é enrolada em torno dele e puxada com uma força de . Supondo que a corda não escorregue, determine (a) o torque exercido pela corda sobre o cilindro, (b) a aceleração angular do cilindro e (c) a rapidez angular do cilindro após .
Ver solução completaQuestão 132
Dois corpos de massa e estão sujeitos à ação da gravidade e são pendurados por cordas na extremidade de uma barra de massa desprezível. A barra é apoiada sobre um ponto distante de uma de suas extremidades e permanece em equilíbrio, como mostrado na figura abaixo. Se a corda de apoio ao bloco é cortada encontre o torque agindo no sistema em relação ao ponto de apoio da barra.
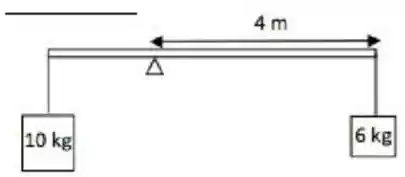
a)
b)
c)
d)
e)
Ver solução completaQuestão 133
Considere uma serra circular movida por um motor. O centro do disco da serra, quando a mesma é usada para cortar madeira, fica submetido a um torque cujo módulo vale . Se, nesta situação, tal disco gira com uma velocidade angular constante de , o trabalho realizado pelo motor em . vale:
a)
b)
c)
d)
e)
Ver solução completaQuestão 134
(Capítulo 9.1 – Exercício 60) Uma roda de amolar está inicialmente em repouso. Um torque externo constante de é aplicado sobre a roda durante , imprimindo à pedra uma rapidez angular de . O torque externo é então retirado, e a roda atinge o repouso depois. Determine (a) o momento de inércia da roda e (b) o torque causado pelo atrito, suposto constante.
Ver solução completaQuestão 135
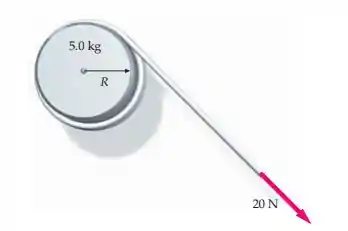
(Cap 9 – Ex 110) Um disco uniforme de tem um raio de e gira livremente em torno de seu eixo. Um cordão, enrolado em volta do disco, é puxado com uma força de . (a) Qual é o torque exercido por esta força em relação ao eixo de rotação? (b) Qual é a aceleração angular do disco? (c) Se o disco parte do repouso, qual é sua rapidez angular após ? (d) Qual é a energia cinética após os ? (e) Qual é o deslocamento angular do disco durante os ? (f) Mostra que o trabalho realizado pelo torque, , é igual à energia cinética.
Questão 136
(Cap 10 – Ex 28) Calcule o torque, em relação à origem, da força gravitacional que atua sobre uma partícula de massa localizada em , e mostre que este torque é independente da coordenada .
Ver solução completaQuestão 137
Uma bola de bilhar recebe uma tacada como indicado na figura. O atrito entre a bola e a mesa é desprezível.
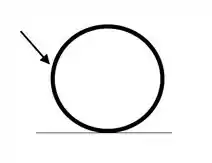
Imediatamente após a tacada, a bola
- Se move para esquerda e gira no sentido anti-horário.
- Se move para direita e giro do sentido anti-horário.
- Se move para esquerda e gira no sentido horário.
- Se move para a direita e gira no sentido horário.
- Se move para a direita e não gira.
Questão 138
Uma haste homogênea de comprimento L e massa M está presa por uma das extremidades a uma parede pelo ponto O. A haste é mantida na horizontal por uma corda que se prende a uma distância igual a 5L/6 e faz um angulo θ = 36,8° com a haste. Sobre a haste existe ainda uma massa pontual m posicionada à distância x do centro de massa da haste. A força da parede sobre a haste está representada na figura como
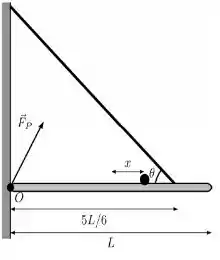
- Calcule a expressão literal para o momento de inércia I do sistema [haste + massa pontual] com relação a um eixo perpendicular à figura que atravessa o ponto O.
- Sabendo que a tensão T na corda não pode exceder 1160 N, encontre o valor máximo de x para que a corda não se rompa.
- Na situação do item (b), encontre o módulo da força que a parede realiza na haste.
- Suponha que a massa m se encontra a um valor x = 0,25m e que a corda se rompeu. No instante que a corda se rompe, calcule a aceleração angular α do sistema.
Nos próximos itens, adote: M = 100 kg, m = 12,0 kg e L = 1,20 m.
Questão 139
Dois discos e de mesmo raio , constituídos de materiais homogêneos, repousam sobre uma mesa horizontal lisa. Aplica-se a mesma forca a cada disco, tangencialmente às suas respectivas periferias, como indica a figura, fazendo-os girar em torno de um pino central no disco e no disco .
Considerando a massa do disco maior do que a massa do disco , as relações entre os módulos dos torques e , em relação a e , devido À força e os módulos das respectivas acelerações angulares resultantes e são dadas por
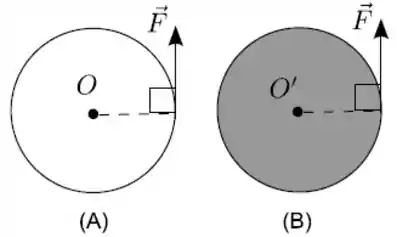
(a) e
(b) e
(c) e
(d) e
(e) e
Ver solução completaQuestão 140
1) Uma placa quadrada de lado tem aplicado em três de seus vértices as forças de mesma intensidade , e cujas orientações são apresentadas na figura, sendo . Ao calcularmos os torques , e produzidos por essas forças em relação ao vértice teremos os seus módulos satisfazendo à seguinte relação:
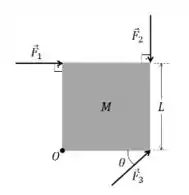
a)
b)
c)
d)
e)
Ver solução completaQuestão 141
O objeto ilustrado ao lado é composto de uma haste rígida de comprimento e de três partículas de massa . Inicialmente ele é mantido em repouso na posição horizontal através de um freio. No instante o freio é retirado e o objeto pode girar livremente em torno do eixo sob ação da força da gravidade. Despreze a massa da haste. Utilize para a aceleração da gravidade.
a) Mostre que o momento de inércia do objeto em torno do eixo é igual a .
b) Determine os torques resultantes e quando a haste ainda estiver na posição horizontal e depois de ter girado radianos.
c) Determine quando a haste ainda estiver na posição horizontal as acelerações lineares e das partículas nas extremidades esquerda e direita da haste.
d) Determine a energia cinética do objeto quando ele estiver passando pela posição vertical e sua aceleração angular nesta mesma posição.
Ver solução completaQuestão 142
O objeto ilustrado ao lado é composto por um cilindro de raio , uma haste rígida e dois discos afastados do eixo de rotação. O objeto tem momento de inércia . Ao longo do perímetro do cilindro está enrolada uma corda inextensível de massa desprezível. Outra parte desta corda está enrolada em uma roldana de raio e momento de inércia . Na extremidade da corda está uma pequeno cubo de massa , distante de um suporte. Não há deslizamento na corda. Inicialmente o sistema é mantido em repouso através de um freio. No instante o freio é retirado e o sistema inicia seu movimento. Utilize para a aceleração da gravidade.
a) Em função das forças indicadas na ilustração, escreva os torques que agem na roldana e no objeto no instante .
Ver solução completaQuestão 143
Um ioiô, disposto como mostrado na figura abaixo, repousa sobre uma superfície sem atrito. Quando uma força é aplicada sobre a corda, o ioiô:
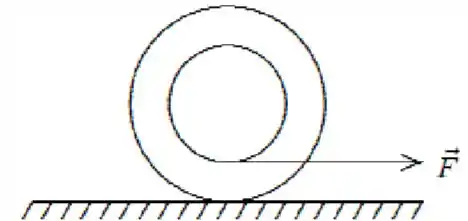
a) move-se para a esquerda e gira no sentido anti-horário.
b) move-se para a direita e gira no sentido anti-horário.
c) move-se para a esquerda e gira no sentido horário.
d) move-se para a direita e gira no sentido horário.
e) move-se para a direita e não gira.
Ver solução completaQuestão 144
Uma esfera desce rolando sem deslizar um plano inclinado. É correto afirmar em relação à força de atrito entre a esfera e a superfície do plano:
- exerce um torque no sentido do deslocamento;
- é nula;
- dissipa energia, por se tratar de uma força de atrito cinética;
- aponta no sentido contrário do deslocamento do Centro de Massa;
- exerce um torque no sentido contrário ao da velocidade angular;
Questão 145
Analise se as afirmações abaixo sobre vetores estão certas ou erradas e assinale a alternativa correta.
Obs.: Essa questão foi alterada em relação a original. Foi retirada as alternativas múltiplas escolha.
- O trabalho realizado por uma força ao longo de um deslocamento é obtido através de um produto escalar . Onde é o ângulo entre e . Portanto, conclui-se que se a força aplicada for perpendicular ao deslocamento, o trabalho realizado será nulo.
- O vetor torque , que expressa a tendência de um corpo sofrer ou alterar seu movimento de rotação, é dado pelo produto vetorial . Onde . O vetor é a distância do ponto de aplicação da força ao eixo de rotação e é o ângulo entre e . Portanto, é possível afirmar que o vetor torque é máximo quando os vetores e forem paralelos.
- Um corpo estará livre de sofrer ou alterar seu movimento de rotação se a força aplicada for perpendicular à direção do vetor .
Questão 146
Um io-iô, disposto como mostrado na figura abaixo, repousa sobre uma superfície sem atrito. Quando uma força é aplicada sobre a corda o io-iô:
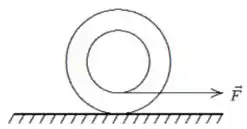
- move-se para a esquerda e gira no sentido anti-horário.
- move-se para a direita e gira no sentido anti-horário.
- move-se para a esquerda e gira no sentido horário.
- move-se para a direita e gira no sentido horário.
- move-se para a direita e não gira.
Questão 147
Uma corda está amarrada à maçaneta de uma porta, vista de cima, que dista 0,72 m do eixo de rotação, conforme figura. No instante mostrado, a força F aplicada possui módulo de 5,0 N. Qual é o torque exercido por esta força sobre a porta?
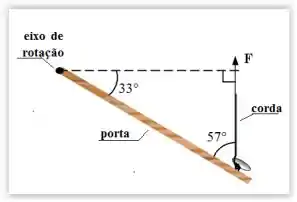
(A) + 2,1 N m
(B) + 3,0 N m
(C) - 3,0 N m
(D) - 1,5 N m
(E) + 1,5 N m
Ver solução completaQuestão 148
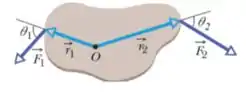
16) O corpo da figura abaixo pode girar em torno de um eixo perpendicular ao plano do papel passando por , e duas forças atuam sobre ele, como mostra a figura. Se , , , , e , qual é o torque resultante em relação ao eixo?
Questão 149
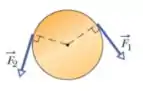
17) A figura abaixo mostra um disco homogêneo que pode girar em torno do centro como um carrossel. O disco tem raio de e massa de , e está inicialmente em repouso. A partir do instante , duas forças devem ser aplicadas tangencialmente à borda do disco, como mostra a figura, para que, no instante , o disco tenha uma velocidade angular de no sentido anti-horário. A força tem um módulo de . Qual é o módulo de ?
Questão 150
Na figura abaixo, uma barra vertical está presa a uma dobradiça na extremidade inferior e a um cabo na extremidade superior. Uma força horizontal é aplicada à barra, como mostrado. Se o ponto de aplicação da força é deslocado para cima ao longo da barra, a tração do cabo aumenta, diminui ou permanece constante?
- depende de quanto o ponto de aplicação da força
- se desloca;
- diminui;
- nada se pode concluir;
- permanece a mesma;
- aumenta;
Questão 151
O comprimento do braço do pedal de uma bicicleta é 0,152m e uma força vertical de 111 N é aplicada ao pedal pelo ciclista. Os valores aproximados do módulo do torque em relação ao eixo do braço do pedal quando o braço faz um ângulo de (a) , (b) e (c) com a vertical são respectivamente:
a) 15 N.m; 0 N.m; 17 N.m
b) 8,4 N.m; 17 N.m; 0 N.m
c) 17 N.m; 0 N.m; 15 N.m
d) 0 N.m; 17 N.m; 8,4 N.m
e) - 11,4 N.m; 23,5 N.m; 35,6 N.m
Ver solução completaQuestão 152
Um cilindro de massa gira em torno de um eixo que passa pelo centro. Sobre ele são aplicadas as forças indicadas na Figura onde e .
Qual é o torque exercido sobre o cilindro?
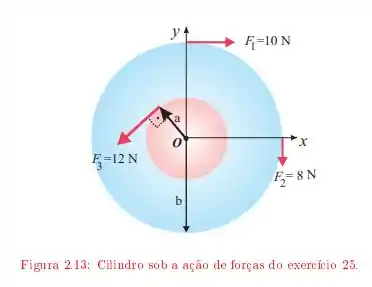
Questão 153
40. Uma bola de futebol, de massa e com diâmetro , rola sem deslizar sobre um plano inclinado. Ela parte do repouso e, depois de e tendo completado exatamente rotações, escapa pela borda do plano inclinado. Dado: .
(a) Calcule o torque resultante sobre a bola relativo ao seu centro de massa, enquanto ela rola sobre o plano inclinado.
Ver solução completaQuestão 154
Uma barra fina rígida, de comprimento e massa distribuída de maneira uniforme ao longo de seu comprimento, está sobre uma mesa horizontal sem atrito, e pode girar em torno de uma de suas extremidades, que está fixada à mesa. Em um determinado instante, são aplicadas três forças à barra . Conforme mostra a figura abaixo, são aplicadas no meio da barra, enquanto é aplicada na extremidade oposta à fixa. As forças são perpendiculares à barra enquanto faz um ângulo , tal que .
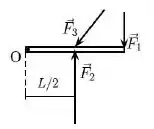
Sobre os módulos dos torques causados por cada uma das forças, em relação ao ponto fixo (O), é válida a relação:
(a) |
(b)
(c)
(d)
(e)
Ver solução completaQuestão 155
O disco de 20 cm de diâmetro mostrado na figura pode girar em torno do eixo que passa pelo seu centro, perpendicular ao disco, com atrito desprezível. As forças mostradas na figura estão aplicadas sobre o disco. Qual o torque resultante sobre o disco em torno do eixo mencionado?
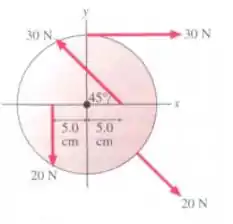
Questão 156
Uma pequena esfera ligada a uma extremidade de uma haste rígida leve gira em torno de um eixo perpendicular que está fixado à outra extremidade da haste. Em um certo sistema de referências, a sua velocidade angular é negativa, e a sua aceleração angular é negativa. Observando o sistema a partir da direção positiva do eixo de rotação, a esfera está:
a) girando no sentido horário e desacelerando.
b) girando no sentido anti-horário e desacelerando.
c) girando no sentido horário e acelerando.
d) girando no sentido anti-horário e acelerando.
e) Primeiro girando no sentido anti-horário e, em seguida, no sentido horário.
Ver solução completaQuestão 157
Calcule o torque resultante sobre um cilindro sob ação das forças de módulo , e em torno do centro, se e . Considere como positivo um vetor apontando para dentro da página e note que a força de módulo é tangente à circunferência interna no ponto em que a mesma intercepta a linha tracejada.
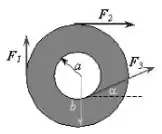
Escolha uma:
- Nenhuma das alternativas
Questão 158
Um quadrado homogêneo de madeira de comprimento de lado é colocado sobre uma mesa horizontal e está livre para girar em torno de seu eixo central. O quadrado está sujeito a duas forças como mostrado na figura. Qual a magnitude do torque resultante sobre o quadrado em relação ao eixo de rotação?
a)
b)
c)
d)
e)
Ver solução completaQuestão 159
Em , um bloco de massa está inicialmente em repouso sobre um plano horizontal e conectado a uma barra rígida de massa desprezível e comprimento que pode girar em torno do ponto O. Um torque é então aplicado à barra, tal que possui uma aceleração angular constante. Existe atrito entre e a superfície horizontal, tal que os coeficientes de atrito estático e cinético são, respectivamente e . Considere .
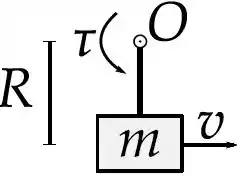
(a) Em que instante de tempo o bloco possui velocidade ?
(b) Encontre o valor do torque aplicado .
Ver solução completaQuestão 160
O caminhão ilustrado abaixo, está com sua lança esticada desde seu eixo até a sua ponta . Sua inclinação é de em relação à horizontal. A massa da lança é e para simplificar os cálculos considere-a uniformemente distribuída. O caminhão está estacionado, com a lança sustentando uma viga de aço de de comprimento e massa , que se encontra na posição horizontal. De forma a manter tudo em equilíbrio estático, um braço hidráulico no topo da cabine de controle, inclinado de em relação à horizontal, atua com uma força no centro de massa da lança . Despreze o atrito da lança com o eixo e as masas dos cabos e do gancho.
Utilize: ; ; ; .
Determine o vetor torque em relação ao eixo exercido pelo braço hidráulico sobre a lança.
Determine o vetor força que atua sobre a extremidade da lança presa ao eixo
Suponha agora que em determinado instante, o braço hidráulico pare de atuar, calcule para este instante o módulo da aceleração angular da lança.
Ver solução completaQuestão 161
Um fio inextensível e de massa desprezível conecta dois blocos, de massas e , onde . O fio passa sem deslizar por um roldana que pode girar sem atrito em torno de um eixo que passa pelo ponto . A roldana tem raio e momento de inércia em relação ao ponto . O sistema é liberado em uma região com aceleração gravitacional . Sabe-se que o módulo da aceleração do sistema, , é não nulo. Sejam e os módulos das trações no fio nos trechos e respectivamente.
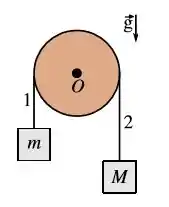
Pode-se afirmar que:
(a)
(b)
(c)
(d)
(e)
(f)
Ver solução completaQuestão 162
Calcule o efeito da massa da polia, de raio , sobre o sistema da figura abaixo. A masssa , que desliza sem atrito está ligado à massa suspensa pelo fio que passa sobre a polia. Determine (a) a aceleração do sistema; (b) as tensões e nos fios ligados a e .
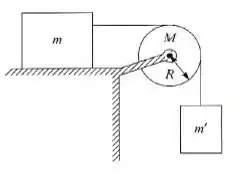
Questão 163
Questão discursiva.
A figura abaixo mostra duas partículas de massa e presas às extremidades de uma barra rígida de massa desprezível e comprimento , com e .
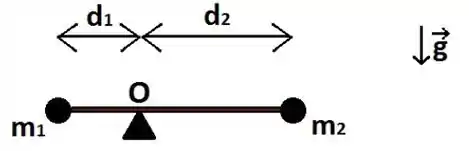
A barra é mantida fixa horizontalmente sobre o ponto , até ser liberada. A partir de então, a barra pode girar em torno de um eixo que passa pelo ponto , perpendicular ao plano da página.
Use .
- Calcule o momento de inérica do sistema em relação ao referido eixo.
- Calcule o módulo do torque resultante em relação ao ponto .
- Determine o módulo da aceleração tangencial de cada partícula assim que a barra é liberada.
Questão 164
Uma bola de 1,0 kg e uma bola de 2,0 kg, presas por um bastão rígido de 1,0 m de comprimento e massa desprezível, giram em torno do centro de massa do sistema no sentido horário a 20 rotações por minuto. Qual o torque necessário para levar o sistema ao repouso em 5,0 s?
Ver solução completaQuestão 165
Se duas forças de mesmo módulo agem sobre um objeto que pode girar em torno de um eixo fixo, a força que age num ponto mais distante do eixo produz o maior torque em relação ao eixo. Esta afirmação
(A) É sempre verdadeira
(B) Nem sempre é verdadeira
(C) É impossível decidir sem saber o momento de inércia do objeto
(D) É impossível decidir sem saber a massa do objeto
(E) É impossível sem saber a forma do objeto
Ver solução completaQuestão 166
Um haltere é formado por duas massas idênticas , presas nas extremidades de uma haste delgada de massa desprezível e de comprimento . Esse haltere está sujeito a duas forças de mesmo módulo , sempre perpendiculares à haste que as une, apontando em sentidos opostos. As forças atuam durante um intervalo de tempo .
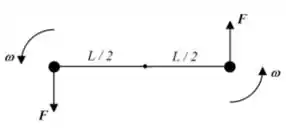
Inicialmente, o haltere está em repouso. Ao fim do intervalo de tempo , a velocidade angular do haltere será
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 167
Um objeto é composto por uma haste de massa desprezível e comprimento ligada ao centro de três discos de massa e raio como ilustra a figura. Este objeto está no plano vertical pode girar livremente em torno do eixo . No instante indicado na figura, a haste encontra-se inclinada de em relação ao eixo . O objeto está em equilíbrio estático, devido à força que tem direção perpendicular à haste. Despreze atritos. A aceleração da gravidade é .
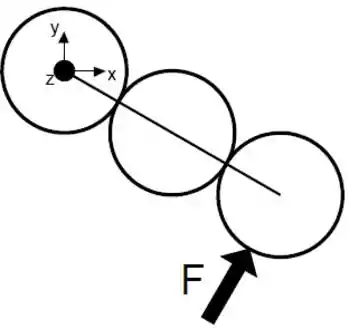
a) Calcule o torque produzido pela força e o torque produzido pela força da gravidade em termos dos dados do enunciado acima.
b) Suponha agora que , e . Em a força desaparece e o torque resultante é dado por . Calcule o módulo da aceleração angular para este instante e também para quando o objeto passar pela posição vertical.
Ver solução completaQuestão 168
Uma corda de massa desprezível e inextensível está enrolada ao redor de um disco uniforme de raio e de massa e possui a outra extremidade fixada numa barra (conforme mostra a figura). O disco, liberado a partir do repouso, cai com a corda na posição vertical e mantém o seu eixo de rotação sempre na mesma direção. Dado: o momento de inercia de um disco de raio e de massa , segundo um eixo que passa pelo seu centro e perpendicular a sua superfície, é igual a .
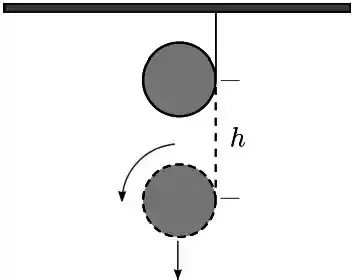
- Determine a aceleração do centro de massa do disco.
- Qual é o módulo da tensão na corda?
- Qual é a velocidade do centro de massa após o disco ter descido uma altura ?
- Qual é a razão entre as energias cinéticas de rotação e de translação , na mesma situação do item c)?
Questão 169
Considere o modelo simplificado de um carro descrito pela figura 1, que possui apenas duas rodas: uma traseira e uma dianteira. A distância entre as duas rodas é dada por . O centro de massa do carro se encontra no ponto de distância de distância da roda traseira. .
a) Sabendo que o carro completo tem massa de , calcule o valor das forças normais: da roda dianteira e na roda traseira , na situação de equilíbrio estático e repouso.
Dados:
Ver solução completa