Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 39.Problemas - Ex. 69
- Usando a integral do problema , determine a função de onda para uma função dada por:
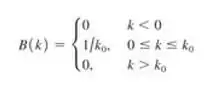
0
e . Portando, representa uma partícula com uma função de onda médio , com um espalhamento toal ou incerteza igual a . Chamaremos esse espalhamento de largura de , logo, .
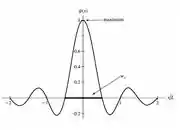
- Faça um gráfico de contra e de contra no caso , onde é um comprimento. Localize o ponto para o qual possui valor máximo e assinale esse ponto sobre o gráfico. Localize os dois pontos mais próximos desse máximo (um para cada lado dele) para os quais e defina a distancia entre esses dois pontos ao longo do eixo a largura de . Indique a distancia no seu gráfico. Qual é o valor de para ?
- Repita o item (b) para o caso .
- O momento linear é igual a , de modo que a largura de no momento linear é . Calcule o produto para cada um dos casos e . Discuta os seus resultados com base na aplicação do principio da incerteza de Heisenberg.
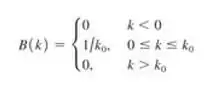
Passo 1
Olá, tudo bem? Vou ajudar você nessa aqui! Vamos lá?
Letra a)
Usando a integral que o enunciado propõe, e sabendo que é nulo fora do intervalo de , a função de onda fica assim ó:
Como é constante, pode sair da integral e daí ficamos com uma integral só com cosseno, que já sabemos resolver =)
Passo 2
Letra b)
O valor máximo dessa função, como vimos no livro texto, vai ser na origem . Isso se dá ao fato de que a função de onda aqui é uma combinação de duas funções: seno e uma hipérbole. O seno fica sempre oscilando entre seus valores máximos e mínimos, e esses são fixos. Já a hipérbole tende ao infinito quando se aproxima do zero, e tende a zero quando aumenta, tanto para mais, quanto para menos infinito.
O resultado dessa combinação é um máximo na origem e um conjunto de picos menores, dos dois lados, se achatando mais à medida que . A função de onda é nula quando temos:
Ou seja, onde , . E a largura dessa função vai ser:
Se tivermos , então a largura fica assim:
O gráfico de contra é uma reta horizontal, pois é constante (com o valor de ) no intervalo de . Tanto antes e depois desse intervalo, é zero. Então o gráfico é assim ó:
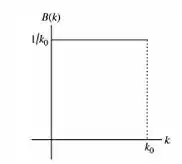
Já o gráfico de contra vai ser como eu expliquei ali em cima: um máximo na origem com o valor de e vai oscilando com a amplitude diminuindo para ambos lados.
Passo 3
Letra c)
Se tivermos o valor da largura vai ser modificado. Resgatando a expressão
Para a largura calculado no item anterior, agora com novo valor para :
Passo 4
Letra d)
Agora vamos calcular o produto . O valor de é . O valor de é . O produto fica:
O principio da incerteza nos diz que . Para o nosso cão, não interessa o valor de , o principio da incerteza é sempre satisfeito =)
Resposta
