a. Use os cálculos feitos nos problemas de 1 a 4 para estimar a dependência radial da autofunção relativa ao estado fundamental do dêuteron num potencial de raio e profundidade .
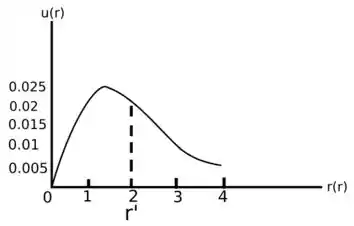
b. Esboce o potencial e a função .
c. Esboce também a densidade de probabilidade radial .
Passo 1
Iremos usar alguns dados importantes dos outros problemas que irei citar durante nossa resolução. Para começar, pegamos os dados do problema 4, tais como: que é a energia de ligação do dêuteron observada experimentalmente, raio , profundidade do potencial , os valores e do problema 2.
Passo 2
As funções obtidas no problema 2 são dadas por:
As condições de contorno impostas no problema 3 nos dão os passos que precisamos para determinar um termo em função de uma única variável.
assim:
.
Essas expressões devem ser as mesmas para . Precisamos de uma relação entre esses termos para que possamos ir adiante. Vamos igualar os termos e encontrar uma relação para C em termos de A.
.
Passo 3
a. Agora com nossas ferramentas em mãos iremos para a parte da funçãoser normalizada de onde foi extraída do problema 1.
(1)
Escrevendo em termos de e aplicando a integral acima, temos
(2)
Obs:
usando a relação:
,
agora substituímos essa relação na equação (2)
(3)
Integral 1
Integral 2
as integrais de e foram resolvidas por substituição.
Entretanto, a equação (2) ainda não foi normalizada. Mas já temos as respostas para que isso aconteça usando as respostas das integrais e substituindo na equação (2).
Com isso, nossa dependência radial é da forma:
.
Resposta
a.
.
b. Consultando o problema 2, o nosso potencial está confinado entre 0 e 2.
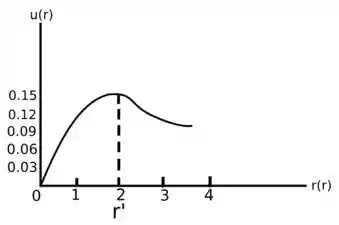
c. A densidade de probabilidade radial também se encontra no mesmo intervalo.