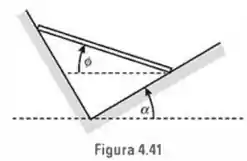
Uma vara de massa de e comprimento é colocada sobre as superfícies planas sem atrito, que formam ângulo reto, conforme mostra a Fig. 4.41. Determine a posição de equilíbrio e as forças de reações, em função do ângulo .
Passo 1
E aí, beleza?? Considere a seguinte figura:
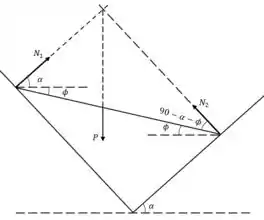
Para determinar as reações normais, vamos escrever o equilíbrio de forças na direção da barra e na direção perpendicular à barra:
Para resolver esse sistema, multiplicamos a primeira equação por e a segunda por e somamos. Assim, eliminamos a força e ficamos com:
Ou seja:
Para resolver a equação para , basta fazer o contrário. Multiplicamos a primeira equação por e a segunda por e, então, subtraímos. Assim, ficamos com:
Portanto:
Passo 2
Agora, para o ângulo , escrevemos o equilíbrio rotacional da barra em torno do ponto de contato da barra com a parede da direita:
Portanto:
Logo: