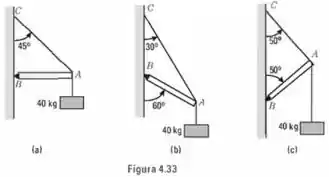
Determine as reações horizontal e vertical (Fig. 4.33) no ponto e a tensão no cabo , admitindo-se que a barra tem a massa de .
Passo 1
E aí, beleza?? Essa questão é uma continuação da questão passada. Assim, considere a seguinte figura:

Vamos novamente escrever a equação do equilíbrio rotacional da barra em torno do ponto :
Portanto, como :
Passo 2
Tomando o equilíbrio de forças na barra nos eixos horizontal e vertical, temos:
Portanto:
Passo 3
Substituindo os valores, em módulo, temos: