Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 32.1 - Ex. 20
Você tem 1,62 m de altura e deseja ver sua imagem completa em um espelho plano vertical.
a) Qual é a altura mínima do espelho que atende à sua necessidade?
b) A que distância acima do solo deve estar a base do espelho em (a), considerando que o topo de sua cabeça esteja a 14 cm acima do nível dos seus olhos? Use um diagrama de raios para explicar sua resposta.
Passo 1
O item a) nos pede a altura mínima do espelho que atende à nossa necessidade de ver nossa imagem completa:
Para responder esse item usaremos apenas uma (e bastante simples) fórmula.
Aplicando os valores:
Passo 2
Para responder o item b), faremos, na maior parte, uma análise, não haverá muitos cálculos.
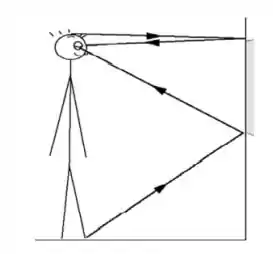
Bem, atenção!
Como queremos a distância mínima, vamos fazer algumas considerações:
A base superior do espelho:
Como a distância dos olhos até o topo da cabeça será de 14 cm, podemos usar a mesma relação usada na letra a):
Portanto, a base superior do espelho pode ficar 7 cm abaixo do topo da cabeça.
A base inferior do espelho:
Como a base superior do espelho ficará 7 cm abaixo do topo da cabeça, o espelho deverá ser posicionado respeitando a seguinte equação:
OBS:
Substraímos da altura da pessoa, o nível superior do espelho e, posteriormente, subtraímos a altura mínima do espelho para que ele possa enxergar todo o seu corpo.
Logo, a base inferior deve estar 74 cm acima do solo.