Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 8.Problemas - Ex. 48

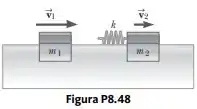
Dois flutuadores planadores são colocados em movimento em um trilho de ar horizontal. Uma mola de constante de força k é presa à extremidade traseira do segundo planador flutuador. Como mostrado na Figura P8.48, o primeiro planador flutuador, de massa m 1 , move-se para a direita com velocidade v 1 , e o segundo planador, de massa m 2 , move-se mais lentamente para a direita com velocidade v 2 . Quando m 1 colide com a mola presa a m 2 , a mola é comprimida por uma distância x m á x , e os flutuadores então se afastam novamente. Em termos de v 1 , v 2 , m 1 , m 2 e k , encontre (a) a velocidade v   na compressão máxima, (b) a compressão máxima x m á x e (c) a velocidade de cada flutuador depois de m 1 perder contato com a mola.

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Letra a:

Quando a mola está totalmente comprimida, cada carrinho se move com a mesma velocidade v. Aplique a conservação do momento para o sistema:

p i = p f :

m 1 v 1 + m 2 v 2 = m 1 + m 2 v → v = m 1 v 1 + m 2 v 2 m 1 + m 2

Passo 2

Letra b:

Apenas as forças conservadoras atuam; portanto, Δ E = 0 :

1 2 m 1 v 1 2 + 1 2 m 1 v 2 2 = 1 2 m 1 + m 2 v 2 + 1 2 k x m 2

x m 2 = 1 k m 1 + m 2 m 1 + m 2 m 1 v 1 2 + m 1 + m 2 m 2 v 2 2 - m 1 v 1 2 - m 2 v 2 2 - 2 m 1 m 2 v 1 v 2

x n t = m 1 m 2 v 1 2 + v 2 2 - 2 v 1 v 2 k m 1 + m 2 = v 1 - v 2 m 1 m 2 k m 1 + m 2

Passo 3

Letra c:

m 1 v 1 + m 2 v 2 = m 1 v 1 f + m 2 v 2 f

A conservação do momento é:

m 1 v 1 - v 1 f = m 2 v 2 f - v 2                   ( 1 )

A conservação de energia é:

1 2 m 1 v 1 2 + 1 2 m 2 v 2 2 = 1 2 m 1 v 1 f 2 + 1 2 m 2 v 2 f 2

m 1 v 1 2 - v 1 f 2 = m 2 v 2 f 2 - v 2 2

m 1 v 1 - v 1 f v 1 + v 1 f = m 2 v 2 f - v 2 ⋅ v 2 f + v 2

E com o uso da equação de momento, temos:

v 1 + v 1 f = v 2 f + v 2

v 1 f = v 2 f + v 2 - v 1                         ( 2 )

Substituindo a equação [2] na equação [1] e simplificando:

v 2 f = 2 m 1 v 1 + m 2 - m 1 v 2 m 1 + m 2

Após a substituição desta expressão na equação [2], temos:

v 1 f = m 1 - m 2 v 1 + 2 m 2 v 2 m 1 + m 2

Resposta

  1. v = m 1 v 1 + m 2 v 2 m 1 + m 2
  2. v 1 - v 2 m 1 m 2 k m 1 + m 2
  3. v 2 f = 2 m 1 v 1 + m 2 - m 1 v 2 m 1 + m 2 ,   v 1 f = m 1 - m 2 v 1 + 2 m 2 v 2 m 1 + m 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco 1 de massa m 1 desliza em um piso sem atrito e sofre uma colisão elástica unidimensional com o bloco 2 de massa m 2=3 m 1 . Antes da colisão, o centro de massa do sistema de dois blocos tinha
Na Fig. 9-67, o bloco 1 de massa m 1 desliza sem velocidade inicial ao longo de uma rampa sem atrito a partir de uma altura h=2,50m e colide com o bloco 2 de massa m 2=2,00 m 1 , inicialmente em repou
Na Fig. 9-64, o bloco A (com uma massa de 1,6k g ) desliza em direção ao bloco B (com uma massa de 2,4k g ) ao longo de uma superfície sem atrito. Os sentidos de três velocidades antes ( i ) e depois
Duas esferas de titânio se aproximam com a mesma velocidade escalar e sofrem uma colisão elástica frontal. Após a colisão, uma das esferas, cuja massa é 300g , permanece em repouso. (a) Qual é a massa
O coeficiente de restituição ϵ de uma colisāo frontal é definido como a razão entre a velocidade relativa depois da colisăo e a velocidade relativa antes da colisão.Qual é o valor de para ϵ uma colisã