Exercícios de Colisões Elásticas - Lista de Exercícios Resolvida

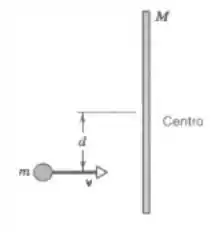
Uma bola de massa , com velocidade de que faz um ângulo de com a horizontal, atinge o centro de uma placa, também de massa , que se encontra inicialmente em repouso. Durante a colisão não há atrito e, devido à colisão, podemos considerar que a placa se move apenas verticalmente. Considerando esta colisão elástica, determine:

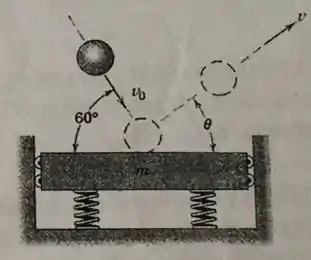
Que grandezas são conservadas nesta colisão. Justifique.

A direção e sentido dos vetores impulso atuando sobre a placa e sobre a bola.

O vetor velocidade final de ambas as massas, bola e placa, logo após o impacto.

O vetor força média que atuou na bola sabendo que o tempo da colisão foi de .

Uma bolinha de massa e velocidade colide com outra bolinha de massa (inicialmente em repouso) como mostra a figura abaixo. Considere que o choque é elástico (a energia mecânica se conserva) e que .

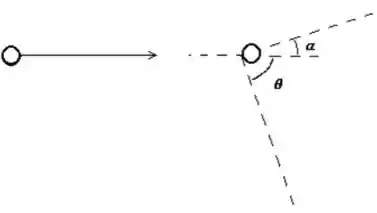
Escreva as equações de conservação de e de .

Calcule as velocidades finais.

Um bloco de massa está em equilíbrio preso a uma mola ideal, de constante elástica , inicialmente em sua posição relaxada, como mostra a figura. Uma bala de massa com velocidade horizontal de módulo colide com esse bloco de modo que a bala retorna após a colisão no sentido oposto com velocidade de módulo .

Considere que: a colisão é instantânea; que a mola é ideal; que a resistência do ar é desprezível; e que a gravidade tem módulo conhecido.

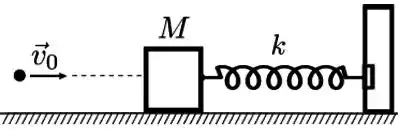
Determine, em função dos dados do problema:

A razão para que a colisão seja elástica.

Dois pêndulos de comprimento estão suspensos juntos conforme a figura abaixo. O pêndulo (de massa ) é solto a partir do repouso de uma altura enquanto que o pêndulo (de massa ) está em repouso na posição vertical.

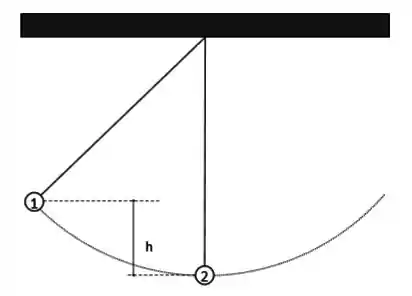
Considerando inicialmente que a colisão é elástica determine:

A velocidade do pêndulo imediatamente antes do choque.

A velocidade de cada pêndulo imediatamente depois do choque.

Dado: .

Considere um choque frontal entre duas bolinhas, como esquematizado na figura abaixo (; ; ; ):

Supondo que a colisão seja elástica (a energia mecânica se conserva), calcule as velocidades após o choque.

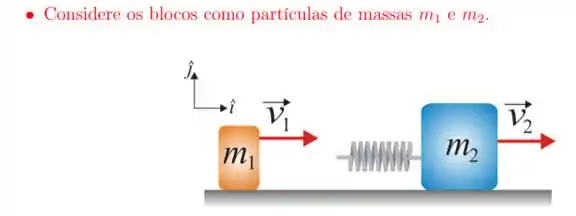
12. Um bloco de massa movimenta-se sobre um trilho horizontal sem atrito com velocidade . Em um dado instante, ele colide com uma mola leve (de massa desprezível), de constante elástica , conectada a um bloco de massa , que se move com velocidade . Sabe-se que na máxima compressão da mola , os blocos têm a mesma velocidade. O valor da máxima compressão da mola, em centímetros, é dada por:

Um próton sofre uma colisão elástica frontal com uma partícula desconhecida que está em repouso. O próton recua com da sua energia cinética inicial. A razão entre as massa da partícula desconhecida e a massa do próton () é:

a)

b)

c)

d)

e)

Um bloco A, com massa de , que estava se movendo com uma velocidade de no sentido positivo de eixo , sofre uma colisão elástica com um bloco , inicialmente em repouso. Se a massa do bloco é muito maior que a do bloco , a velocidade do bloco após a colisão é:

1. Zero.

Um cavaleiro de move-se a da esquerda para a direita sobre um trilho de ar horizontal sem atrito. Ele colide frontalmente com um cavaleiro de que se move a da direita para a esquerda. Supondo colisão elástica, determine o módulo, a direção e o sentido de cada cavaleiro depois da colisão.

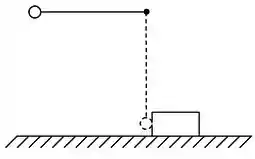
Uma bola de massa é presa a um pino por um fio leve e inextensível de 0,8 m de

comprimento. A bola é abandonada quando o fio está na horizontal. Na parte mais baixa da sua trajetória, a bola atinge um bloco de massa , inicialmente em repouso sobre uma superfície áspera. A colisao entre eles pode ser considerada perfeitamente elástica. O coeficiente de atrito cinético entre o bloco e a superfície é . Considere a aceleração gravitacional .

1. Qual é o trabalho realizado por cada força atuando sobre a bola até o momento logo antes da colisão?
2. Qual é a velocidade de cada corpo depois da colisão?
3. Até que altura sobe a bola após a colisão?
4. Qual é o trabalho realizado pela força de atrito sobre o bloco até parar?
5. Qual é a distância percorrida pelo bloco?

Dentro de uma câmara, temos uma névoa formada por gotículas d'água em suspensão, com uma densidade . Considere um cubo de massa M, se deslocando horizontalmente sem atrito sobre um trilho neste ambiente, com uma velocidade inicial de módulo e direção perpendicular a uma de suas faces, de área A. Despreze a resistência com o ar e o atrito com o trilho.

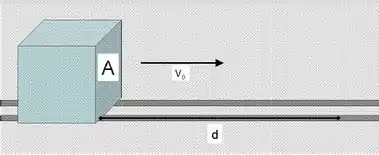
1. Se o corpo absorver a água ao longo de sua passagem, apenas pela face frontal, percorrendo uma distância , qual vai ser sua velocidade final?

b) Qual a variação de energia do sistema?

c)Considere agora que no lugar de gotículas d'água, temos cristais de gelo, que sofrem colisões elásticas com a superfície do corpo. Considerando que a densidade da névoa é a mesma do caso anterior, qual a velocidade do corpo, decorrido um tempo do início do deslocamento?

Dê suas respostas em termos

Um nêutron de massa colide de frente com um núcleo de deutério

inicialmente em repouso. A massa do deutério é o dobro da do nêutron, ou seja, . Se a velocidade do nêutron antes da colisão é é a colisão é elástica e unidimensional, determine:

(a) As velocidades e do nêutron e do núcleo de deutério depois da colisão.

(b) A energia cinética total do sistema.

Num piso sem atrito, um bloco colide frontalmente com outro bloco que estava em repouso. Os gráficos ao lado representam quatro possibilidades para a variação da energia cinética de cada bloco em função do tempo, desde antes até depois da colisão. Qual(ais) gráfico(s) pode(m) representar uma colisão elástica?

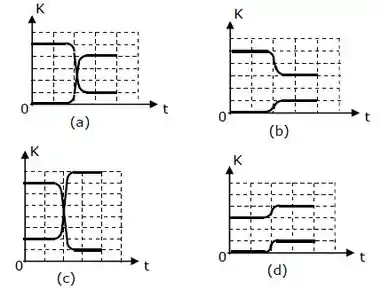
(A) Tanto (a) quanto (b).

(B) Tanto (a) quanto (c).

(C) Tanto (a) quanto (d).

(D) Somente (d).

(E) Somente (a).

Dois objetos se encontram sobre uma superfície horizontal sem atrito. Um objeto de 2,50 kg de massa colide elasticamente com outro de 3,60 kg que, inicialmente, está em repouso. O objeto mais leve possui, após a colisão, uma rapidez de 4,00 m/s e se move formando um ângulo em relação à sua direção original; o objeto mais pesado possui uma rapidez de 2,50 m/s e se move formando um ângulo , conforme é mostrado na figura.

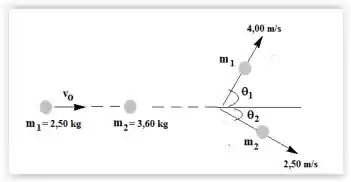
(a) Explique se o momento do objeto mais leve se conserva ou não.

(b) Determine a rapidez inicial do objeto mais leve.

(c) Calcule os ângulos e

Considere dois blocos inicialmente parados nas extremidades de uma rampa sem atrito como ilustrado na figura abaixo. O bloco vermelho tem massa e energia , enquanto o bloco azul tem massa e energia . Os blocos são soltos e ao alcançarem a superfície plana da rampa toda a energia está em forma de energia cinética.

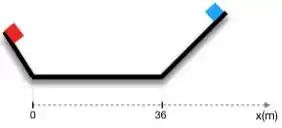
Calcule a posição onde os blocos sofrerão uma colisão.

Considere uma colisão perfeitamente elástica entre os blocos. Calcule as velocidades finais de cada bloco e o coeficiente de restituição da colisão.

Esboce, num único gráfico, a energia cinética de cada bloco e a energia cinética do sistema em termos da posição na parte plana da rampa.

Você observa um carro a colidindo frontalmente com uma bola de tênis, lançada contra ele a . Você observa que a bola é rebatida pelo carro na mesma direção na qual ela incidiu. A velocidade final da bola observada por você será aproximadamente de:

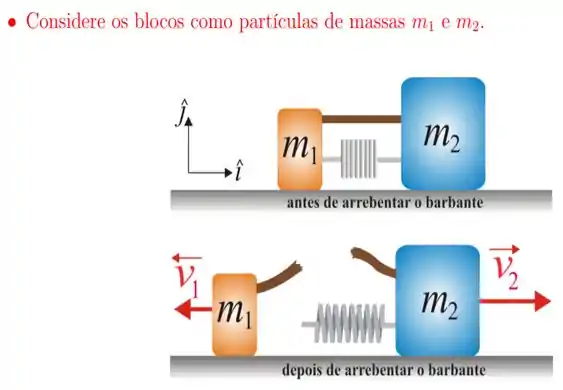
10. Dois blocos de massas e estão parados sobre uma superfície horizontal sem atrito. Uma mola leve (de massa desprezível), comprimida, é presa a um dos blocos. Um barbante que inicialmente mantém os blocos juntos arrebenta-se; depois disso, o bloco de massa move-se com velocidade , e o bloco de massa move-se com velocidade . A energia potencial elástica antes do barbante arrebentar, em Joules, é:

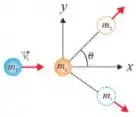
Q - Uma partícula de massa se movimenta com velocidade e colide elasticamente com uma partícula em repouso de massa como mostrado na figura. Após a colisão, é observado que as duas partículas têm mesma componente dos vetores velocidade. Determine o módulo do vetor velocidade da partícula de massa , em , imediatamente após a colisão.

Q - Dois patinadores, de massas e , deslizam em linha reta sobre uma pista de gelo sem atrito, estando de mãos dadas. A velocidade dos patinadores é , enquanto eles andam de mão dadas. Num determinado instante eles se empurram e o patinador de massa passa a deslizar com velocidade e o

de massa passa a mover-se com velocidade . Nestas condições, a energia fornecida pelo

empurrão, em Joules, é:

• Considere os patinadores como partículas.

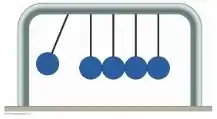
Q - Considere o dispositivo da figura, chamado de pêndulo de Newton. Todas as colisões entre as bolas no dispositivo são elásticas.

Se uma bola em um extremo é puxada para trás e solta, como mostrado na figura, haverá uma quebra da conservação de momento se duas bolas no outro extremo se moverem com metade da velocidade da primeira bola?

O resultado do evento em será uma quebra da conservação de energia?

Mostre que o único resultado consistente com a conservação de momento e a conservação de energia é que se bolas forem puxadas para trás e soltas, bolas deverão subir do outro lado.

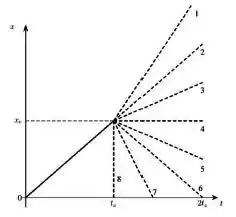
Uma pequena esfera de massa desliza ao longo do eixo x em uma mesa horizontal sem atrito e colide elasticamente, frontalmente, com uma outra esfera, de massa > , que estava inicialmente em repouso (a colisão é unidimensional). O gráfico abaixo mostra a posição da esfera de massa em função do tempo até o instante da colisão , que ocorre na posição (linha sólida). Qual a reta tracejada indicada no gráfico que representa a evolução da posição da esfera de massa m após a colisão?

1. 5
2. 1
3. 2
4. 3
5. 4
6. 6
7. 7
8. 8

Um elétron colide, elasticamente, com um átomo de hidrogênio que está inicialmente em repouso. Suponha todo o movimento ocorrendo ao longo de uma linha reta. Qual fração da energia cinética inicial do elétron é transferida para o átomo? (Tome a massa do átomo de hidrogênio como vezes a massa de um elétron).

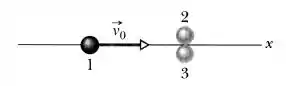
As três bolas da figura são idênticas. As bolas 2 e 3 estão se tocando e alinhadas perpendicularmente à trajetória da bola 1. A velocidade da bola 1 tem módulo e está dirigida para o ponto de contato das bolas 2 e 3. Após a colisão, quais são

(a) o módulo e

(b) a orientação da velocidade da bola 2,

(c) o módulo e

(d) a orientação da velocidade da bola 3 e

(e) o módulo e

(f) a orientação da velocidade da bola 1?

(Sugestão: sem atrito, cada impulso está dirigido ao longo da reta que liga os centros das bolas envolvidas na colisão e é perpendicular às superfícies que se tocam.)

Uma barra de comprimento e massa repousa sobre uma mesa horizontal sem atrito. Um pequeno objeto de massa movendo-se com velocidade , como mostra a figura ao lado (visão de cima), colide elasticamente com a barra a uma distância de seu centro.

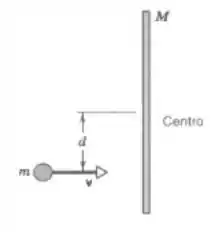
b) Qual deve ser a massa do objeto para que ele fique em repouso após a colisão? DICA: Aplique as leis de conservação enunciadas no item anterior, e considere que no final a barra irá transladar + girar em torno de um eixo que passa pelo próprio centro de massa dela.

Considere uma colisão frontal (de maneira que o movimento ocorre em uma única dimensão) entre duas partículas, de massas e . Inicialmente a partícula de massa encontra-se em repouso enquanto a de massa se move com velocidade . Sabendo que a colisão é elástica, pode-se afirmar que, após a colisão:

(a) A partícula de massa passa ao repouso enquanto a de massa passa a se mover com velocidade .

(b) A partícula de massa passa ao repouso enquanto a de massa passa a se mover com velocidade .

(c) A partícula de massa passa a se mover com velocidade no sentido contrário ao de ao passo que a de massa se move com velocidade no mesmo sentido de .

(d) Ambas as partícula se movem com velocidades no mesmo sentido de .

(e) A partícula de massa passa ao repouso enquanto a de massa passa a se mover com velocidade .

Num jogo de bilhar, um jogador deseja colocar a bola roxa/escura na caçapa, como mostrado na figura. Se o ângulo da caçapa é , em que ângulo a bola branca é defletida? Considere que a colisão é elástica e despreze o atrito e o movimento de rotação das bolas, e considere bolas de massas iguais.

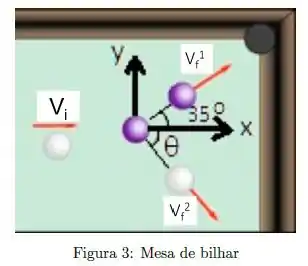
(A) .

(B) 50.

(C) .

(D) .

(E) .

Dois objetos constituem um sistema isolado. Em uma colisão elástica entre os dois objetos, qual das seguintes afirmações pode ser falsa?

(a) A energia cinética de cada objeto é a mesma antes e depois da colisão.

(b) Os módulos das forças exercidas durante a colisão por cada objeto no outro são iguais entre si.

(c) O momento linear do sistema é o mesmo antes e depois da colisão.

(d) A energia cinética total do sistema é conservada.

(e) O módulo do impulso que o objeto A faz no B é igual ao que o B faz no A.

Uma partícula (1) de massa se move na direção positiva do eixo com velocidade no topo de uma mesa sem atrito de altura . Ao final da mesa encontra-se uma partícula (2) de massa . Ignore a dimensão das partículas.

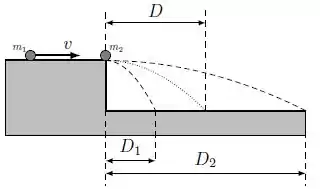
a) Supondo que a partícula (1) colide com a partícula (2) elasticamente como é descrito na figura, encontre a distância total percorrida por cada partícula em relação a base da mesa (na figura as distâncias são representadas por e , suas trajetórias são descritas pelas linhas tracejadas). O tempo de queda é .

Duas bolas e , de massas e diferentes, colidem elasticamente. Inicialmente a bola tem velocidade , onde é uma constante positiva, e a bola está em repouso. Após a colisão a bola passa a se mover com velocidade , na direção perpendicular à direção do movimento inicial. Considere o plano da colisão como sendo horizontal e despreze as forças de atrito.

(a) Faça um esboço dos vetores velocidades das bolas e após a colisão, indicando o sistema de coordenadas e os ângulos envolvidos.

(b) Escreva o sistema de equações que a partir do qual é possível determinar a direção e a magnitude da velocidade da bola após a colisão. Justifique cada uma destas equações.

(c) Determine o ângulo entre e a direção .

(d) Determine o vetor e seu módulo em função de .

Um próton sofre uma colisão elástica frontal com uma partícula desconhecida que está em repouso. O próton recua com da sua energia cinética inicial. A razão entre as massa da partícula desconhecida e a massa do próton é:

(A)

(b)

(C)

(D)

(E)

A partícula , de massa , desliza para a direita ao longo do eixo em um piso sem atrito com uma velocidade escalar de . Quando chega ao ponto no instante , ela sofre uma colisão elástica unidimensional com a partícula de massa , que estava inicialmente em repouso, conforme a figura ao lado.

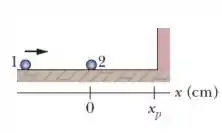
Quais as velocidades finais das partículas e após essa colisão?

Um disco de massa colide com um bloco de massa na ausência de forças externas. Após a colisão, o bloco adquire momento linear na direção e a componente do momento linear do disco é conservada (veja a figura abaixo).

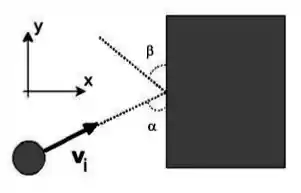
Admitindo que a colisão é elástica, se , a componente da velocidade final do disco pode ser escrita em termos da componente da sua velocidade inicial como:

nenhuma das outras alternativas.

Uma partícula de massa desloca-se num plano horizontal, sem atrito, com velocidade . Sabe-se ainda que ela colide com uma segunda partícula de massa , inicialmente em repouso.Sendo o choque unidimensional e elástico, determine suas velocidades após o choque.

a) e

b) e

c) e

d) e

e) e

Uma bola de bilhar de está inicialmente em repouso quando recebe o impacto de uma segunda bola de mesma massa. Verificamos que após o impacto a bola passou a se movimentar com velocidade de e a bola ficou em repouso. Considerando o choque perfeitamente elástico, determine a quantidade de movimento da bola .

(a)

(b)

(c)

(d)

(e)

Uma bola de massa m, movendo -se com velocidade para a direita, choca–se com outra bola de massa , inicialmente em repouso. Após colidirem, a bola adquire uma velocidade de para a direita. Determine a velocidade final da bola .

Uma bola de tênis, com massa desconhecida, é lançada com velocidade =37,5 i [m/s] e colide, elásticamente, contra uma parede, a força da colisão na parede, dada pelo gráfico ao lado, produz um impulso sobre a bola J= 4,5 Kg.m/s (-i). A força máxima na colisão é =2250 N e ocorre em Δtc/2. Determine:

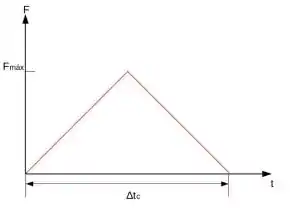
1. O vetor velocidade da bola após perder o contato com a parede.
2. A massa da bola.
3. O tempo da colisão.
4. Variação da energia cinética do sistema bola-parede entre os instantes imediatamente antes da colisão e imediatamente depois de deixar o contato com a parede.
5. Variação do momento linear da bola entre os instantes imediatamente antes da colisão e imediatamente depois de deixar o contato com a parede.

A partícula , de massa , desliza para a direita ao longo do eixo em um piso sem atrito com uma velocidade escalar de . Quando chega ao ponto no instante , ela sofre uma colisão elástica unidimensional com a partícula de massa , que estava inicialmente em repouso, conforme a figura ao lado.

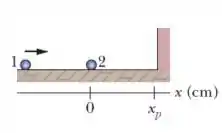
Após a colisão, a partícula se chocará com uma parede localizada no ponto (ver figura acima). Considerando essa colisão elástica, e a massa da parede muito maior que a da partícula , qual a velocidade da partícula após essa colisão dela com a parede?

Após colidir com a parede, a partícula irá colidir novamente com a partícula ? Se sim, calcule em que posição e em que instante essa nova colisão irá ocorrer, e calcule também as novas velocidades finais de e após essa colisão (considerando colisão elástica). Se não, justifique.

Uma haste fina e homogênea , de massa e comprimento , é livre para girar numa mesa de ar horizontal (sem atrito) em torno de um eixo vertical que passa pela extremidade . Uma bola rígida de massa é lançada com velocidade contra a extremidade enquanto a haste está em repouso. A colisão é elástica e a bola fica em repouso imediatamente após a colisão.

Dado: o momento de inércia da haste em relação ao eixo de rotação é .

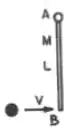
1. Determine a massa da bola em termos da massa da haste.
2. O momento linear do sistema bola haste se conserva na colisão? Justifique sua resposta.

Um sistema isolado é constituído por uma partícula A de massa com velocidade inicial constante de módulo v e por uma partícula B inicialmente em repouso. Após colidirem elasticamente, ambas permanecem na reta do movimento inicial da partícula A, que passa a ter uma velocidade de módulo no mesmo sentido do seu movimento inicial. A massa da partícula B é:

Amplificador de velocidade. Na figura, o bloco 1, de massa , desliza ao longo de um eixo em um piso sem atrito, com uma velocidade , até sofrer uma colisão elástica unidimensional com o bloco 2, de massa , inicialmente em repouso. Em seguida, o bloco 2 sofre uma colisão elástica unidimensional com o bloco 3 de massa , inicialmente em repouso.

1. Qual é a velocidade final do bloco 3?

Comparados aos valores iniciais do bloco 1,

(b) A velocidade,

(c) a energia cinética e

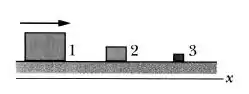(d), o momento do bloco 3 são maiores, menores ou iguais?

Uma barra de comprimento e massa repousa sobre uma mesa horizontal sem atrito. Um pequeno objeto de massa movendo-se com velocidade , como mostra a figura ao lado (visão de cima), colide elasticamente com a barra a uma distância de seu centro.

a) Quais grandezas são conservadas na colisão? Justifique sua resposta.

Um corpo de massa desce, a partir do repouso, uma rampa semiesférica de raio sem atrito, partindo da mesma altura do centro rampa. Ao chegar no ponto mais baixo ele colide com outro corpo de massa que se encontrava ali em repouso. Considere a colisão elástica e com . Encontre a altura que o corpo 2 sobe em função de .

Tome .

As duas massas à direita, e conforme mostra figura abaixo, estão ligeiramente separadas e inicialmente em repouso; a massa da esquerda incide sobre as outras duas com velocidade . Supondo que as colisões sejam diretas e elásticas:

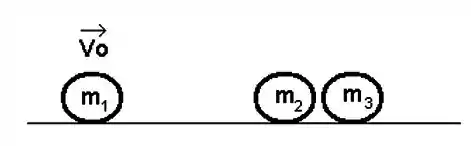
(a) Achar a velocidade que a segunda massa adquire. Considerar o choque elástico e frontal.

(b) Achar a velocidade que a última massa adquire.

(c) Mantendo e constantes, calcule o valor de para que a velocidade do terceiro corpo seja máxima.

(Cap 9 – Ex 66) Uma bola de aço de massa está presa em uma extremidade de uma corda de de comprimento. A outra extremidade está fixa. A bola é liberada quando a corda está na horizontal (Fig. 9-68). Na parte mais baixa da trajetória, a bola se choca com um bloco de metal de inicialmente em repouso sobre uma superfície sem atrito. A colisão é elástica. Determine

(a) a velocidade escalar da bola e

(b) a velocidade escalar do bloco, ambas imediatamente após a colisão.

O gráfico mostra a velocidade dos corpos A e B antes, durante e depois de uma colisão. A afirmação correta é:

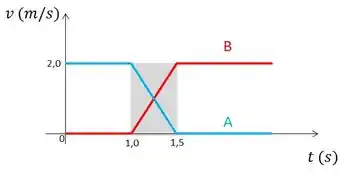
(a) A Energia Cinética não se conserva.

(b) A colisão é perfeitamente elástica.

(c) A velocidade inicial de A é igual à velocidade inicial de B.

(d) O coeficiente de restituição é igual à 0.

(e) Existe uma força externa atuando no sistema.

Q - Em um certo referencial inercial, uma partícula, de massa movimentando-se com velocidade sobre uma superfície horizontal, colide elasticamente com uma partícula de massa que está parada. Considerando que o movimento das partículas após a colisão continua sendo ao longo do eixo , o módulo do vetor velocidade (em ) da partícula de massa imediatamente depois da colisão, no referencial centro de massa, é:

Um projétil de atinge um bloco de pendurado em um pêndulo erguendo-o a de sua posição horizontal. Determine aproximadamente a velocidade inicial do projétil.

()

OBS: Utilize conservação da quantidade de movimento e conservação da energia mecânica.

(Cap 9 – Ex 67) O bloco 1 de massa desliza em um piso sem atrito e sofre uma colisão elástica unidimensional com o bloco 2 de massa . Antes da colisão, o centro de massa do sistema de dois blocos tinha uma velocidade de . Qual é a velocidade

(a) do centro de massa e

(b) do bloco 2 após a colisão?

(Cap 9 – Ex 70) Na Fig. 9-71, o disco 1, de massa , desliza sem atrito em uma bancada de laboratório até sofrer uma colisão unidimensional com o disco 2, inicialmente em repouso. O disco 2 é arremessado para fora da bancada e vai cair a uma distância da base da bancada. A colisão faz o disco 1 inverter o movimento e ser arremessado para fora da outra extremidade da bancada, indo cair a uma distância da base oposta. Qual é a massa do disco 2? (Sugestão: tome cuidado com os sinais.)

(Cap 9 – Ex 69) Uma pequena esfera de massa está verticalmente acima de uma bola maior de massa (com uma pequena separação, como no caso das bolas de beisebol e basquete da Fig.9-70a) e as duas bolas são deixadas cair simultaneamente de uma altura . (Suponha que os raios das bola são desprezíveis em comparação com .)

(a) Se a bola maior ricocheteia elasticamente no chão e depois a bola menor ricocheteia elasticamente na maior, que valor de faz com que a bola maior pare momentaneamente no instante em que colide com a menor?

(b) Nesse caso, que altura atinge a bola menor (Fig. 9-70b)?

(Cap 9 – Ex 63) Um corpo com de massa sofre uma colisão elástica com um corpo em repouso e continua a se mover na mesma direção e sentido, mas com um quarto da velocidade inicial.

(a) Qual é a massa do outro corpo?

(b) Qual é a velocidade do centro de massa dos dois corpos se a velocidade inicial do corpo de era ?

(Cap 9 – Ex 62) Na Fig. 9-66, o bloco (com uma massa de ) desliza em direção ao bloco (com uma massa de ) ao longo de uma superfície sem atrito. Os sentidos de três velocidades antes () e depois () da colisão estão indicados; as velocidades escalares correspondentes são , e . Determine

(a) o módulo e

(b) o sentido (para a esquerda ou para a direita) da velocidade ·

(c) A colisão é elástica?

Um bloco de massa deslizando sobre uma mesa horizontal, com coeficiente de atrito cinético colide com uma mola de massa desprezível, de constante de mola inicialmente na posição relaxada. O bloco atinge a mola com velocidade de .

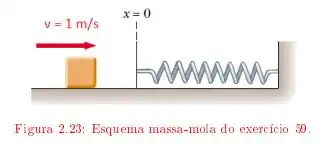
Que acontece depois que a mola atinge a sua deformação máxima?

Um bloco de massa deslizando sobre uma mesa horizontal, com coeficiente de atrito cinético colide com uma mola de massa desprezível, de constante de mola inicialmente na posição relaxada. O bloco atinge a mola com velocidade de .

c) Que fração da energia inicial é dissipada pelo atrito nesse processo?

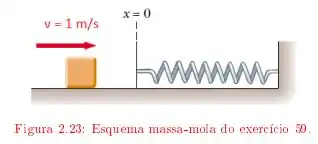
Um bloco de massa deslizando sobre uma mesa horizontal, com coeficiente de atrito cinético colide com uma mola de massa desprezível, de constante de mola inicialmente na posição relaxada. O bloco atinge a mola com velocidade de .

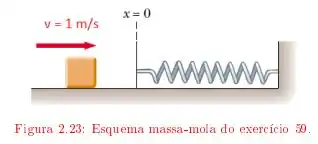
Qual é a deformação máxima da mola?

Um vagão , de massa , move-se com velocidade igual a sobre trilhos horizontais sem atrito até colidir com outro vagão , de massa , inicialmente em repouso. Após a colisão, o vagão fica parado. A energia cinética final do vagão B vale:

(a)

(b)

(c)

(d)

(e)

Redija uma definição para os termos citados a seguir:

- conservação de momento

- colisão totalmente elástica

- colisão totalmente inelástica

Um projétil de é disparado horizontalmente com velocidade em , contra um corpo de massa suspenso por um fio de de comprimento. Em um choque perfeitamente elástico e frontal, o corpo sobe até uma altura . Qual é o ângulo máximo formado pelo fio com a vertical?

Em um experimento, um projétil de massa e velocidade atinge um bloco de massa suspenso por um fio e inicialmente em repouso. Depois da colisão, o projétil se aloja no bloco e o conjunto atinge uma altura

1. Calcule a altura .
2. Calcule a energia dissipada na colisão.

Em outro experimento, uma bola de massa e velocidade colide elasticamente com um bloco de massa suspenso por um fio e inicialmente em repouso. O bloco então atinge uma altura .

3. Calcule a razão entre as alturas e .

Um bloco de massa está em equilíbrio preso a uma mola ideal, de constante elástica , inicialmente em sua posição relaxada, como mostra a figura. Uma bala de massa com velocidade horizontal de módulo colide com esse bloco de modo que a bala retorna após a colisão no sentido oposto com velocidade de módulo .

Considere que: a colisão é instantânea; que a mola é ideal; que a resistência do ar é desprezível; e que a gravidade tem módulo conhecido.

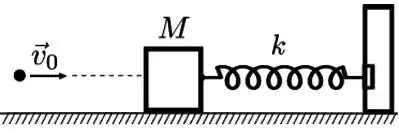
Determine, em função dos dados do problema:

a) a velocidade do bloco de massa imediatamente após a colisão.

b) a compressão máxima da mola.

c) a razão para que a colisão seja elástica.

Um bloco de massa desliza sobre uma superfície horizontal sem atrito com velocidade de e colide com outro bloco de massa em repouso. A colisão é perfeitamente elástica, os blocos ficam em contato por e o bloco tem velocidade de com sentido oposto ao da velocidade inicial. A intensidade da força média exercida pelo bloco sobre durante o contato é:

Dois carros, sendo um compacto com massa de e o outro um grande consumidor de gasolina com massa de, colidem frontalmente a velocidades típicas de estrada. (a) Qual carro possui maior módulo de variação no momento linear? Qual carro possui maior variação na velocidade? (b) Considerando que o carro maior altere sua velocidade em , calcule a variação na velocidade do carro menor em termos de . (c) Os ocupantes de qual dos carros sofrerão lesões mais graves? Explique.

A energia interna de um sistema isolado permanece constante, embora possa ser convertida entre diferentes tipos de energia. Esta afirmação trata do princípio de conservação da energia, um princípio fundamental da física. Tendo em mente o princípio de conservação da energia, considere uma colisão entre duas bolas sobre uma mesa de bilhar. Após a colisão, as bolas perdem energia pela ação do atrito até pararem. Considere que a colisão entre as bolas seja elástica, e que a perda de energia cinética das bolas pelo atrito com a mesa se dê exclusivamente por aquecimento (energia térmica). O que se pode dizer a respeito da conservação da energia desde o instante imediatamente anterior à colisão até o instante em que as bolas param?

(A) A energia total do sistema composto pelas duas bolas se conserva, enquanto a energia mecânica deste sistema é conservada apenas durante a colisão.

(B) A energia total do sistema composto pelas duas bolas não se conserva. Tampouco a energia mecânica deste sistema é conservada durante a colisão.

(C) A energia total do sistema composto pelas duas bolas e pela mesa de bilhar se conserva, mas a energia mecânica deste sistema não é conservada durante a colisão.

(D) A energia total do sistema composto pelas duas bolas e pela mesa de bilhar se conserva, enquanto a energia mecânica deste sistema é conservada apenas durante a colisão.

(E) A energia total do sistema composto pelas duas bolas e pela mesa de bilhar não se conserva. Tampouco a energia mecânica deste sistema é conservada durante a colisão

Um pequeno disco de massa se move sobre uma mesa horizontal sem atrito com velocidade constante de módulo , quando sofre uma colisão unidimensional elástica com outro objeto de massa , inicialmente em repouso. Considerando o módulo do momento linear e a energia cinética do sistema formado pelos dois discos após a colisão é correto afirmar que:

(a) e

(b) e

(c) e

(d) e

(e) (a) e

(f) e

(g) e

Considere uma colisão frontal (de maneira que o movimento ocorre apenas em uma dimensão) entre duas partículas de massas e . Inicialmente a partícula de massa move-se com velocidade e a de massa com velocidade . Sabendo que a colisão é elástica, após a colisão, as velocidades das partículas de massa e serão, respectivamente:

(a) e

(b) 0 e

(c) 0 e

(d) e

(e) e

Em uma colisão elástica, uma partícula de e velocidade atinge outra partícula de massa , e que seguia na mesma direção com velocidade de . As velocidades finais das partículas são respectivamente:

não há como calcular as velocidades sem informações sobre se o momento linear é conservado.

Dois blocos de massas iguais deslizam sobre uma superfície horizontal de maneira que o atrito entre eles e a superfície é desprezível. O movimento acontece na presença do campo gravitacional terrestre. Os módulos das velocidades iniciais dos blocos são tais que . O bloco carrega consigo uma mola (ver figura abaixo) de constante elástica cuja massa é desprezível.

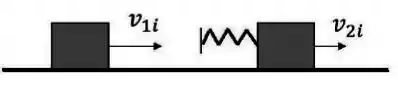
No instante em que a compressão da mola é máxima, podemos afirmar que

o momento linear total é idêntico ao da situação inicial mas a energia cinética não.

o momento linear total é idêntico ao da situação inicial e a energia cinética também.

o momento linear total não é idêntico ao da situação inicial mas a energia mecânica sim.

o momento linear total não é idêntico ao da situação inicial e a energia potencial elástica aumentou.

nenhuma das outras alternativas.

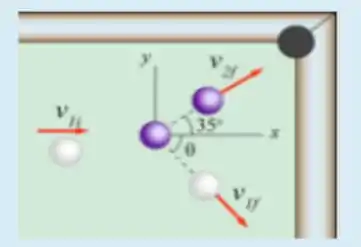
Num jogo de bilhar, um jogador deseja colocar a bola roxa, inicialmente em repouso, na caçapa. Para tal lança uma bola branca, que colide com a bola roxa, como mostrado na figura. Se o ângulo que a direção inicial da bola branca faz com a trajetória da bola roxa é 35º. Em que ângulo a bola branca é defletida?

Considere que a colisão é elástica e que as bolas têm mesma massa. Despreze o atrito e o movimento de rotação das bolas.

a) 35º;

b) 55º;

c) 90º;

d) 25º;

e) 45º

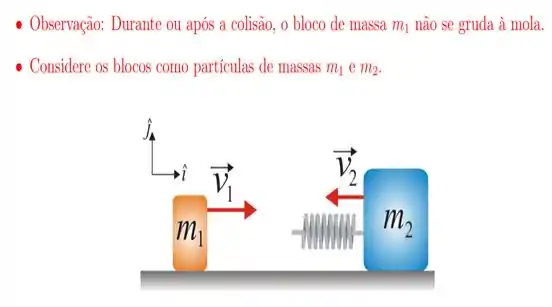
11. Um bloco de massa movimenta-se sobre um trilho horizontal sem atrito com velocidade . Em um dado instante, ele colide com uma mola leve (de massa desprezível) conectada a um bloco de massa , que se move com velocidade . Durante o processo de colisão, quando a velocidade do bloco é , a energia potencial elástica armazenada na mola é:

Q – Um bloco de inércia se desloca com velocidade e atinge uma mola que esta presa a um segundo bloco de inércia que tem velocidade . A inércia da mola é desprezível em relação às outras inércias. A mola é comprimida e depois volta a sua posição normal sem dissipar energia.

Quais são as velocidades finais dos dois blocos?

Que fração da energia cinética inicial o bloco perde?

No caso particular onde , faça o gráfico da fração versus e comente as situações para , e .

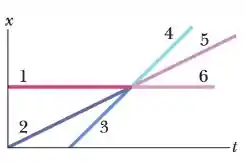
Dois corpos sofrem uma colisão elástica unidimensional ao longo de um eixo . A figura mostra a posição dos corpos e do centro de massa em função do tempo quando estes entram na região . Pode-se dizer que:

(a) A massa do corpo que estava se movendo mais depressa antes da colisão é igual à do outro corpo.

(b) As retas e representam os movimentos dos corpos depois da colisão.

(c) Os dois corpos estavam se movendo antes da colisão.

(d) A reta representa o movimento do centro de massa antes da colisão.

(e) A massa do corpo que estava se movendo mais depressa antes da colisão é maior que a do outro corpo.

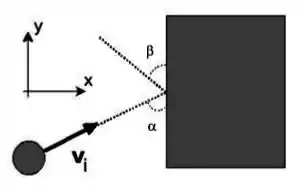
Um disco de massa colide com um bloco de massa na ausência de forças externas. Após a colisão, o bloco adquire momento linear na direção e a componente do momento linear do disco é conservada (veja a figura abaixo). Admitindo que a colisão é elástica, podemos afirmar que:

o ângulo de incidência do disco é igual ao ângulo de reflexão .

o ângulo de reflexão não depende da relação das massas do disco e do bloco.

o ângulo de reflexão é menor que o ângulo de incidência .

o ângulo de reflexão é maior que o ângulo de incidência .

o ângulo de reflexão é zero.

Dois blocos se movem sobre uma superfície horizontal sem atrito, conforme indicado na figura. O bloco de , inicialmente movendo-se para a direita com rapidez de , colide com o segundo bloco de , que está inicialmente movendo-se para esquerda com rapidez de . Após a colisão, o bloco de move-se para a esquerda, com rapidez , e o bloco de passa a se mover para a direita, com rapidez de . Esta colisão pode ser caracterizada como:

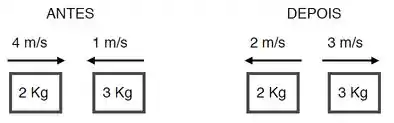
(A) perfeitamente elástica.

(B) parcialmente elástica.

(C) completamente inelástica.

(D) caracterizada por um aumento da energia cinética.

(E) não é possível caracterizar a colisão, pois o momento linear não foi conservado.

Uma bolha de bilhar se move a uma velocidde de e colide com uma bola de massa igual, inicialmente em repouso. Se a primeira bola para após a colisão, a segunda bola se moverá com uma velocidade de:

A.

B.

C.

D.

E.

Um átomo de hidrogênio , movendo-se com velocidade , colide elasticamente com uma molécula de hidrogênio em repouso, sofrendo uma deflexão de .

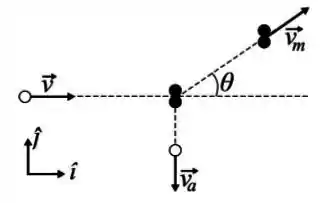
(a) Calcule o valor numérico do ângulo , em graus, da figura entre a direção do movimento da molécula após a colisão e a direção inicial de movimento do átomo.

(b) Calcule os módulos das velocidades do átomo e da molécula após a colisão em termos de .