Apoios Elásticos
Produzido por Pablo RicardoTeoria
Introdução
Algumas estruturas que estivermos estudando, podem acabar tendo apoios elásticos, que nada mais são que apoios que se deformam. Para isso precisamos primeiro saber como identificar esses apoios, e em seguida saber como trata-los em estruturas isostáticas e hiperestáticas.
- Os tipos de apoios elásticos.
Podemos ter 3 tipos de apoios elásticos, que são.
- Mola vertical (que pode ser representada por):
- Mola horizontal (que pode ser representada por):
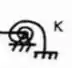
- Mola para momentos fletores (que pode ser representada por):
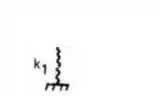
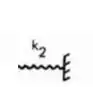
- Molas verticais e horizontais sempre irão virar apoios do primeiro gênero
- Molas do tipo engaste elástico sempre irão virar apoios com momentos fletores, podendo ser carrinhos ou engastes dependendo da situação.
As fórmulas para cálculo das deformações
As fórmulas para cálculo da deformação das molas, são muito simples, e elas sempre serão somadas as deformações que já aprendemos calcular, elas basicamente se dividem em dois grupos. O primeiro grupo das molas verticais, ou horizontais, que podemos determinar a sua equação usando o nosso velho conceito de trabalhos virtuais, tendo dessa maneira que a nossa fórmula será dada por:
Em que sabemos que é a força na nossa mola no sistema com a carga unitária, e é a deformação na nossa mola, e lembra como determinar a deformação na mola pela física 1?
E lembre-se que é a força real que age na nossa mola, sendo assim podemos escrever a nossa fórmula como:
E vamos ver que no futuro, para conseguirmos relacionar essa fórmula com o resto da conta, iremos precisar do termo então para já ficarmos tranquilos com isso podemos multiplicar ambos os lados da equação, obtendo assim a nossa fórmula final.
E se seguirmos esse mesmo processo, conseguiremos chegar na fórmula final para o segundo grupo de molas, que são as molas do tipo engaste elástico, que podemos seguir da seguinte maneira.
Logo
Que multiplicando ambos os lados por obteremos a nossa equação final dada por:
Agora a pergunta mais importante é: como aplicamos esse conceito a uma estrutura isostática e uma estrutura hiperetática?
As estruturas isostáticas
Vamos supor que tenhamos o seguinte problema em mãos:
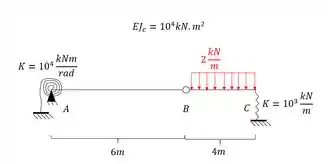
E desejemos saber o valor da rotação em B. Como começaríamos a fazer isso?
Passo 1 – transformar o sistema de molas em um sistema equivalente
Nós não sabemos trabalhar bem com molas, mas sabemos trabalhar muito bem com apoios, por isso vale lembrar sempre a seguinte regrinha.
No nosso exemplo, podemos ver que temos uma mola vertical do lado direito, que irá virar um apoio do primeiro gênero. E uma mola do tipo engaste elástico do lado esquerdo, que junto com o apoio do segundo gênero irá equivaler a um engaste.
Sendo assim a nossa estrutura equivalente será:
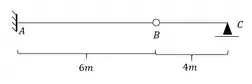
Passo 2 – desenhar o diagrama do carregamento real
Perceba que nesse nosso primeiro exemplo a estrutura de fato é isostática. E agora basta fazermos o que já sabemos para determinar a deformação normal dessa estrutura, sabemos que o primeiro diagrama a ser determinado é o de momentos fletores devido a carga real na nossa estrutura, que será dada por:
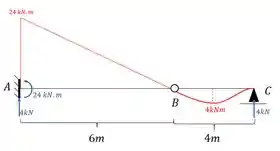
Perceba que também colocamos as reações de apoio que vão ser bem importantes pra gente.
A partir desse gráfico, podemos analisar cada item do enunciado separadamente.
Passo 3 – desenhar o diagrama do sistema com a carga unitária
- Rotação a elástica do ponto B
- Deformação relacionada a mola em C
- Deformação relacionada a mola em A
- Deformação total será a soma de todas as parcelas contribuintes da deformação.
- Sabemos que molas verticais e horizontais viram apoios do primeiro gênero
- Sabemos que molas do tipo engaste elástico viram apoios com momento
Como já temos o diagrama com carregamento real, precisamos do diagrama colocando no ponto B um momento que represente a rotação a elástica em uma rótula, dessa maneira o nosso sistema será:
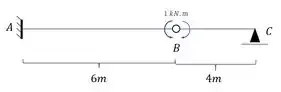
E o diagrama será dado por:
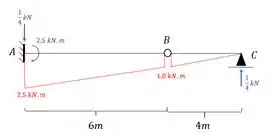
Passo 4 – Cálculo das deformações
Se combinarmos esses dois diagramas vamos ter que:
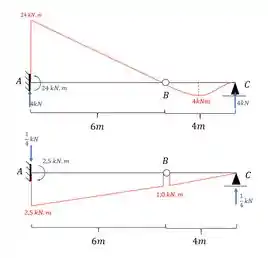
Mas perceba que isso são as deformações apenas relativas ao diagrama de momentos, vamos agora contabilizar o que se refere as molas.
Como se trata de uma mola vertical, sabemos que a sua fórmula é dada por.
Sabemos que:
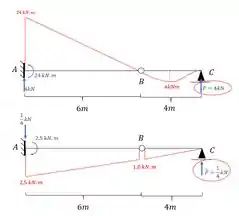
Substituindo teremos que:
Como se trata de uma mola do tipo engaste elástico, sabemos que a sua fórmula é dada por.
Sabemos que:
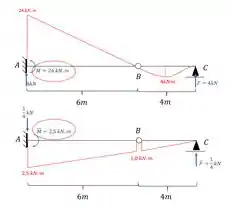
Substituindo teremos que:
A Estrutura hiperestática
Nas estruturas hiperestáticas vamos seguir exatamente os mesmos princípios da estrutura isostática, mas lembrando algumas regrinhas.
Para isso vamos ver um segundo exemplo.
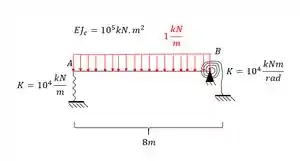
Já sabemos que a primeira coisa que devemos fazer é transformar esse sistema em um sistema equivalente.
Dessa maneira nosso sistema equivalente será.
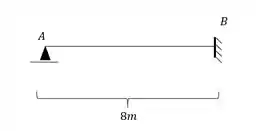
Perceba que esse sistema equivalente tem 1 apoio do terceiro gênero e 1 do primeiro gênero, totalizando 4 incógnitas. Sabemos também que temos as 3 equações de equilíbrio, e nenhuma rotula, sendo assim, teremos um total de 1 hiperestático, ou seja, precisamos usar as nossas regrinhas para estruturas hiperestáticas.
Sabemos que como temos um hiperestático, devemos quebrar um vínculo, e quebrando esse vínculo, a estrutura vai ser isostática. Sendo assim a nossa estrutura principal será dada por.
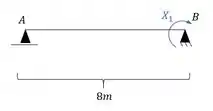
E perceba que daqui para frente as regras são todas as que já sabemos sobre estruturas hiperestáticas.
- Diagrama da estrutura com o carregamento externo
- Diagrama no sistema 1 com carregamento hiperestático unitário
- Deformação
- Deformação
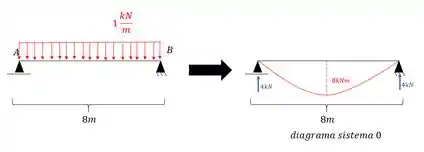
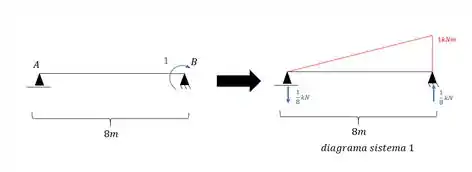
E agora precisamos determinar as deformações, e aqui que temos que tomar cuidado. Vamos começar com a deformação zero:
Sabemos que essa deformação vai ter a parcela relativa a combinação de diagramas, devido a mola vertical e devido a mola tipo engaste elástico, dessa maneira a nossa sequencia será dada por:
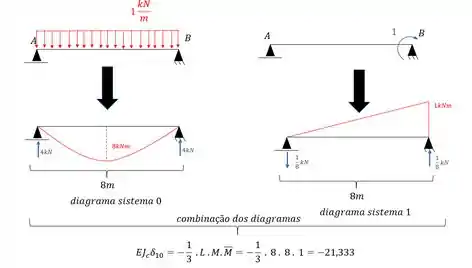
Feita a contribuição dos diagramas, vamos fazer agora a analise e contribuição das molas:
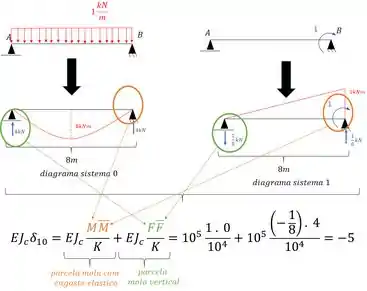
Agora só precisamos somar as duas parcelas contribuídas, e assim teremos que:
Sabemos que essa deformação vai ter a parcela relativa a combinação de diagramas, devido a mola vertical e devido a mola tipo engaste elástico, dessa maneira a nossa sequencia será dada por:
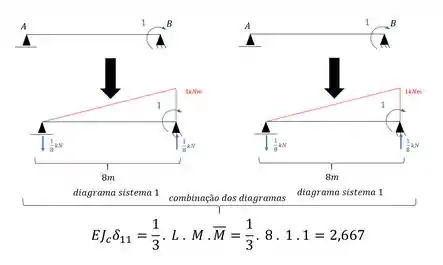
Feita a contribuição dos diagramas, vamos fazer agora a análise e contribuição das molas:
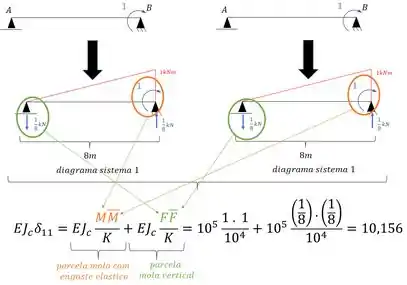
Agora só precisamos somar as duas parcelas contribuídas, e assim teremos que:
E agora, por fim, só precisamos resolver o nosso velho amigo sistema de equações que é dado por:
Substituindo teremos que:
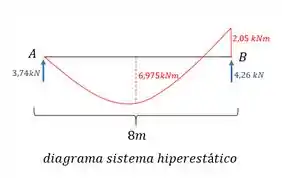
Determinação dos diagramas e das reações de apoio
Precisamos analisar os dois diagramas, e para isso devemos ter eles em mãos.
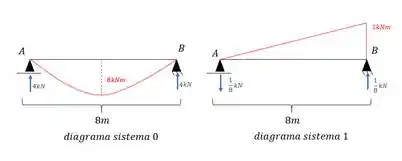
Para as reações de apoio usamos
Para os momentos teremos que
Passo 3 – desenhar o diagrama do sistema com a carga unitária
Passo 4 – Cálculo das deformações
A Estrutura hiperestática
Determinação dos diagramas e das reações de apoio
Exercícios Resolvidos
Exercício Resolvido #1
Origem do Exercício
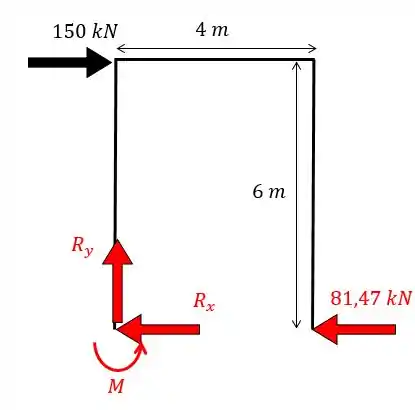
Determine a rotação do ponto A e o deslocamento vertical do ponto B da estrutura dada abaixo.
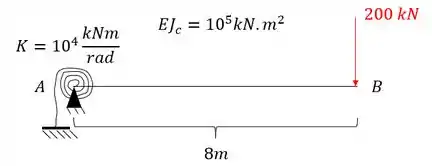
Passo 1
Nós não sabemos trabalhar bem com molas, mas sabemos trabalhar muito bem com apoios, por isso vale lembrar sempre a seguinte regrinha.
- Molas verticais e horizontais sempre irão virar apoios do primeiro gênero
- Molas do tipo engaste elástico sempre irão virar apoios com momentos fletores, podendo ser carrinhos ou engastes dependendo da situação.
No nosso exemplo, podemos ver que temos uma mola do tipo engaste elástico do lado esquerdo, que junto com o apoio do segundo gênero irá equivaler a um engaste.
Sendo assim a nossa estrutura equivalente será:
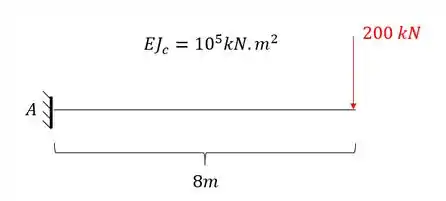
Passo 2
Perceba que nesse nosso primeiro exemplo a estrutura de fato é isostática. E agora basta fazermos o que já sabemos para determinar a deformação normal dessa estrutura, sabemos que o primeiro diagrama a ser determinado é o de momentos fletores devido a carga real na nossa estrutura, que será dada por:
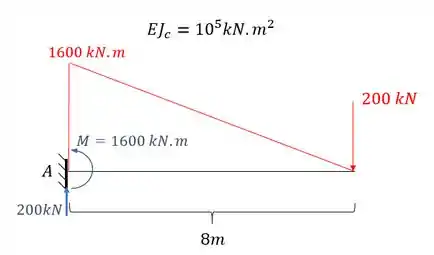
Perceba que também colocamos as reações de apoio que vão ser bem importantes pra gente.
A partir desse gráfico, podemos analisar cada item do enunciado separadamente.
Passo 3
O primeiro objetivo é determinar a rotação do ponto A.
- Rotação no ponto A
- Deformação relacionada a mola em A
- Deformação total será a soma de todas as parcelas contribuintes da deformação.
- Deslocamento vertical no ponto B
- Deformação da mola em A devido uma carga em B
- Deformação total será a soma de todas as parcelas contribuintes da deformação.
Como já temos o diagrama com carregamento real, precisamos do diagrama colocando no ponto A um momento que represente a rotação no ponto A:
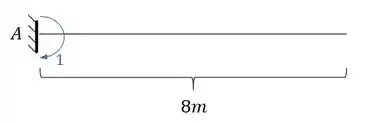
E o diagrama será dado por:
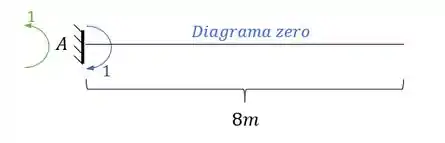
E perceba que o diagrama nesse caso será zero. Mas as reações de apoio para nós serão importantes.
Passo 4
Perceba que se combinarmos os diagramas teremos que:
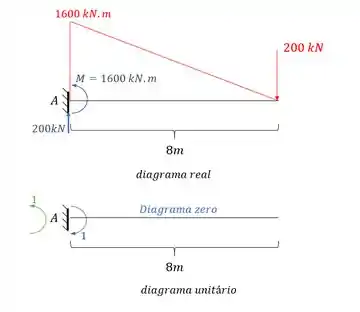
Mas perceba que isso são as deformações apenas relativas ao diagrama de momentos, vamos agora contabilizar o que se refere as molas, ou seja, em um primeiro momento isso pode parecer que a rotação será zero. Mas precisamos tomar cuidado, porque temos a mola, sendo assim teremos que.
Como se trata de uma mola do tipo engaste elástico, sabemos que a sua fórmula é dada por.
Sabemos que:
Substituindo teremos que:
Passo 5
O segundo objetivo é determinar o deslocamento vertical em B.
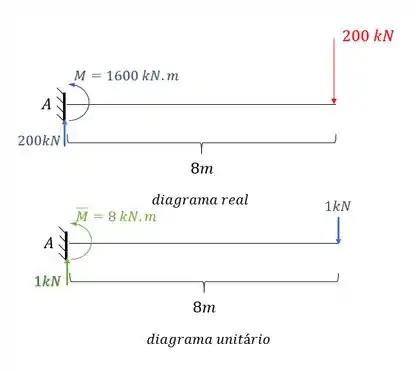
Como já temos o diagrama com carregamento real, precisamos do diagrama colocando no ponto B uma carga vertical que represente o deslocamento no ponto B:
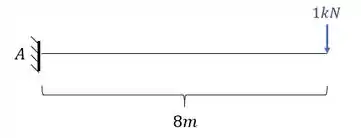
E o diagrama será dado por:
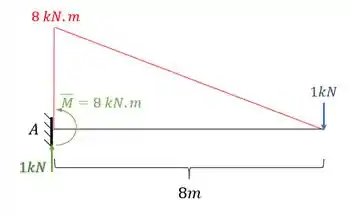
Passo 6
Perceba que se combinarmos os diagramas teremos que:
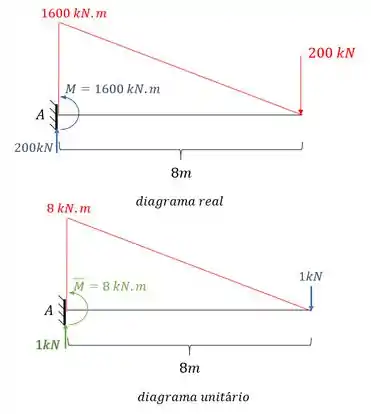
Como se trata de uma mola do tipo engaste elástico, sabemos que a sua fórmula é dada por.
Sabemos que:
Substituindo teremos que:
Resposta
Exercício Resolvido #2
Origem do Exercício
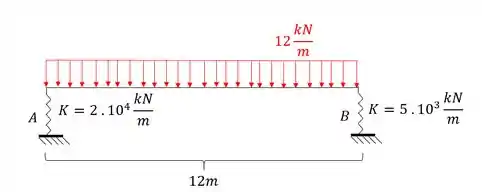
Determine o diagrama de deslocamentos verticais da viga dada abaixo, determinando pelo menos 3 pontos deslocados.
Passo 1
Antes de determinar qualquer coisa precisamos antes determinar os pontos que iremos determinar os deslocamentos, que nesse caso iremos usar estrategicamente os apoios e o ponto central da estrutura.
Passo 2
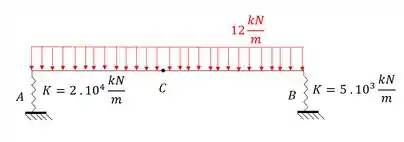
Em seguida sabemos que o que devemos fazer é determinar o sistema equivalente que iremos usar na nossa estrutura.
Como só temos molas verticais, teremos apenas apoios verticais, e como não temos forças horizontais, não iremos nós preocupar com o que ocorre na horizontal, sendo assim o nosso sistema será dado por:

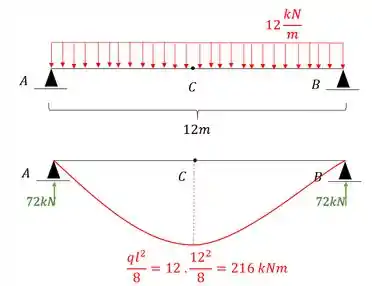
Sabemos que antes de começar a usar qualquer fórmula precisamos garantir logo o nosso diagrama para esse sistema equivalente com o carregamento externo, sendo assim, teremos que o nosso diagrama será:
Passo 3
Agora precisamos descobrir o deslocamento de cada um dos pontos que tivermos definido. Perceba que como temos que descobrir os deslocamentos dos apoios, é melhor começarmos exatamente por eles, dessa maneira teremos que:
- Apoio em A
- Apoio em B
- Deformação em C
Para descobrirmos o deslocamento vertical nele, precisamos por uma carga unitária no ponto em que queremos saber e na direção que queremos saber, dessa maneira teremos que:
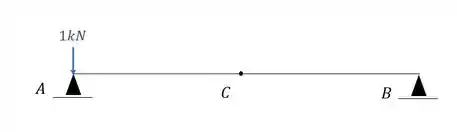
Perceba que esse diagrama será zero, logo, qualquer combinação entre diagrama será inútil para ver se tem deslocamento, pois já sabemos que nesse caso a combinação será zero.
Em contra partida temos as reações de apoio que serão dadas por.
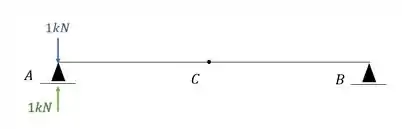
Porque a reação de apoio é importante para nós? Exatamente porque sabemos que a fórmula para determinar a deformação na mola é:
Sabemos que:
E perceba que consideramos a contribuição das duas molas, é que nesse caso a reação em uma será zero, e por esse motivo será desprezada, mas substituindo o que temos na fórmula teremos que:
Para descobrirmos o deslocamento vertical nele, precisamos por uma carga unitária no ponto em que queremos saber e na direção que queremos saber, dessa maneira teremos que:

Perceba que esse diagrama será zero, logo, qualquer combinação entre diagrama será inútil para ver se tem deslocamento, pois já sabemos que nesse caso a combinação será zero.
Em contra partida temos as reações de apoio que serão dadas por.
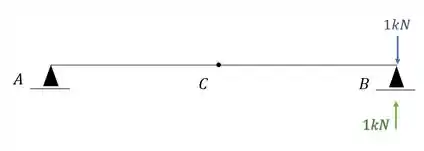
Porque a reação de apoio é importante para nós? Exatamente porque sabemos que a fórmula para determinar a deformação na mola é:
Sabemos que:
E perceba que consideramos a contribuição das duas molas, é que nesse caso a reação em uma será zero, e por esse motivo será desprezada, mas substituindo o que temos na fórmula teremos que:
Passo 4
Para descobrirmos o deslocamento vertical nele, precisamos por uma carga unitária no ponto em que queremos saber e na direção que queremos saber, dessa maneira teremos que:
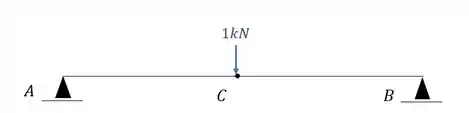
Agora nesse caso iremos ter sim diagrama, e nesse caso o diagrama junto com as reações de apoio será dado por:
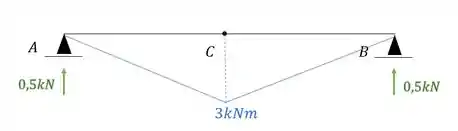
E devemos combinar ele com o diagrama de carregamentos reais que é dado por:
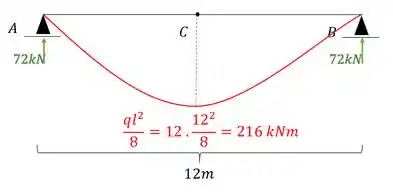
É usando a nossa tabela de combinações, sabemos que a combinação desses dois diagramas resulta em:
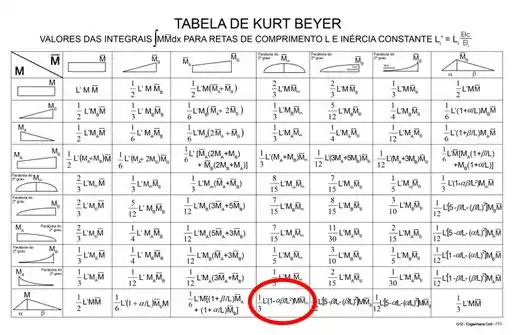
Também temos as reações de apoio que serão dadas por.

Porque a reação de apoio é importante para nós? Exatamente porque sabemos que a fórmula para determinar a deformação na mola é:
Sabemos que:
E perceba que consideramos a contribuição das duas molas, substituindo o que temos na fórmula teremos que:
Logo a deformação total em C será a soma das duas parcelas dadas por:
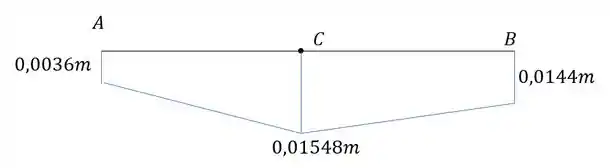
Tendo todas as deformações teremos que o nosso diagrama será:
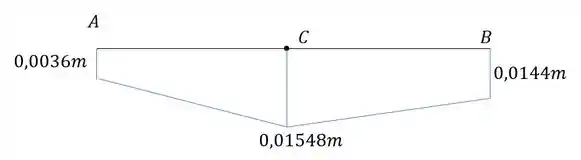
Resposta
Exercício Resolvido #3
Elaboração própria
Calcule as reações nos apoios e da viga abaixo sabendo que a viga está apoiada por uma mola linear em e uma mola de rotação em . Dado: ; ;
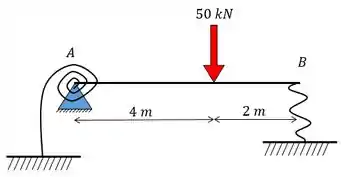
Passo 1
Pessoal, vamos resolver essa questãozinha que tem uma viga em condição hiperestática e possui duas molas, como dito no enunciado. Uhullll
A primeira coisa que a gente tem que lembrar é que vamos retirar as molas e substituir por apoios fixos. Dessa forma a nossa resolução fica mais fácil pois resolvermos um problema hiperestático normal. Depois, lá no final do problema a gente calcula a parcela relativa aos apoios elásticos e soma tudo.
Vamos ver com calma tudo isso, partiu!
Passo 2
Vamos retirar as molas e substituí-las por outros tipos de apoio. Para isso a gente tem que lembrar que a mola de rotação é substituída por um apoio do tipo engaste ou carrinho. Como o apoio é de segundo gênero então vamos substituir por um engaste.
Já a mola linear será substituída por um apoio de primeiro gênero. Assim, vamos obter:
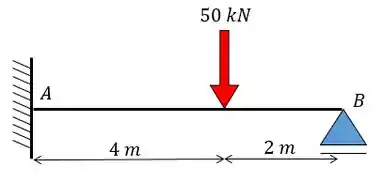
Pronto! Chegamos no nosso problema hiperestático convencional. Agora vamos resolvê-lo normalmente.
Passo 3
Este problema hiperestático possui um grau de hiperestaticidade, então vamos quebrar um vínculo (pode ser qualquer um, eu vou quebrar o apoio porque eu acho ele boboca) a gente só precisa lembrar que temos de colocar uma força equivalente. Dessa forma vamos obter:
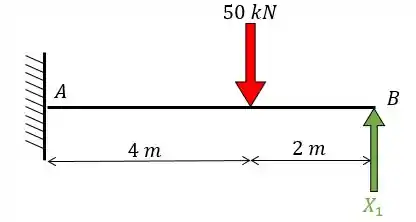
Eis que temos o nosso hiperestático e agora o que temos que fazer é achar o valor desse “indivíduo” escrutável... Para isso vamos dividir o problema em dois sistemas e fazer os seus respectivos diagramas de momento fletor.
Ps: Como, ao dividirmos o problema em dois sistemas, a gente obtém sistemas isostáticos, não vou perder muito tempo fazendo as contas não ok? Só vou mostrar como que fica o resultado para vocês =D
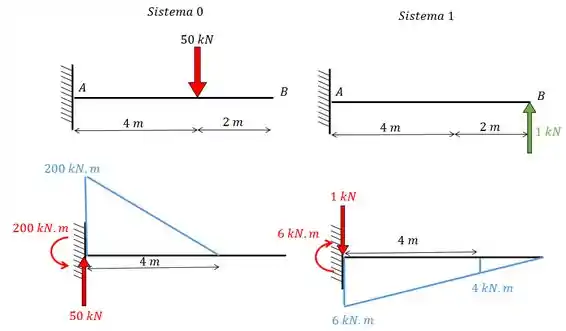
Viram como eu sou bonzinho e além de colocar o diagrama do momento fletor (em azul) ainda coloquei as forças resultantes (em vermelho). Owwnnnnn, que fofis....
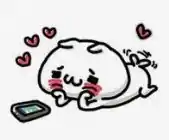
Passo 4
Agora a gente tem que lembrar de como calcular o nosso hiperestático . A gente faz isso através da equação do deslocamento que tem a seguinte forma:
Então a gente vai precisar achar a deformação do sistema 0 em relação ao sistema 1 () e do sistema 1 em relação a ele mesmo (). Lembrando que vamos fazer isso com ajuda daquela nossa tabelinha marota.
Então vamos lá! Primeiro vamos calcular , aqui a gente precisa ficar ligado porque pode parecer que é a combinação de dois triângulos, mas na verdade é um triângulo e um trapézio. Isso acontece porque no sistema 0 o diagrama acaba em assim o triângulo do sistema 1 vira um trapézio =D
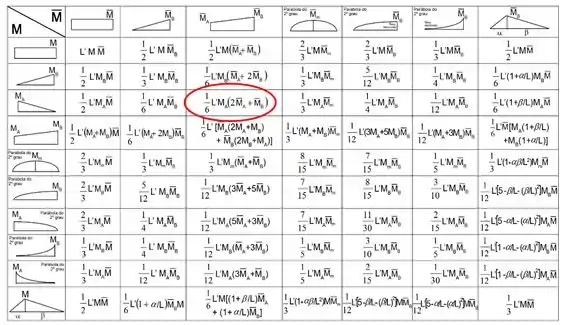
A tabela mostra a combinação de um triângulo com um trapézio:
Substituindo nós vamos ter:
Observe que há um sinal negativo que é introduzido devido aos sentidos opostos do momento fletor.
Agora para , dessa vez são dois triângulos mesmo:
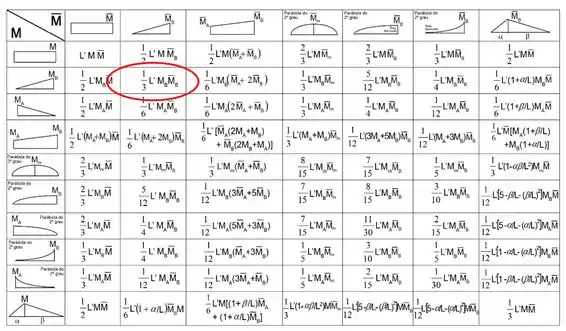
Pessoal, achamos os valores de e já podemos substituir na expressão abaixo?
A resposta é não =(
Por que a resposta é não? Porque se fizéssemos isso então a gente não estaria considerando a parte dos apoios elásticos, que até agora ainda não apareceram... Vamos ver como eles aparecem.
Passo 5
Para considerarmos a parte relativa aos apoios elásticos nós vamos calcular um novo e um novo , vamos chamá-los de e . Esses novos termos são as deformações de cada apoio elástico e são dados por aquelas equações que vimos na teoria:
Vamos olhar novamente as reações da nossa viga:
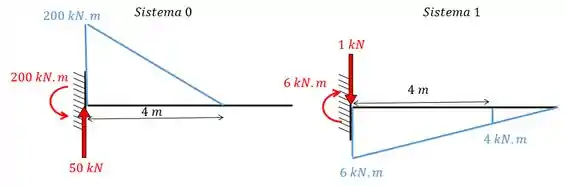
Com as reações vamos poder calcular os valores e .
Agora vamos fazer a substituição:
Para vamos ter:
Substituindo:
Passo 6
Agora podemos finalmente utilizar a equação para achar o nosso hiperestático . Para isso vamos somar os seguintes valores:
E vamos obter:
Obtendo.
E finalmente podemos substituir na equação do hiperestático:
Passo 7
Dessa forma vamos ter:
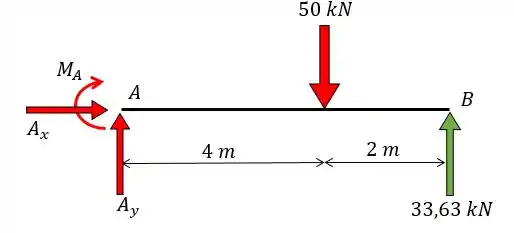
Nós achamos o nosso hiperestático que é
Pelas equações da estáticas vamos achar:
Resposta
Exercício Resolvido #4
Elaboração própria
Calcule as reações nos apoios e da viga abaixo sabendo que a viga está apoiada por duas molas lineares horizontais e duas verticais. Dado:;
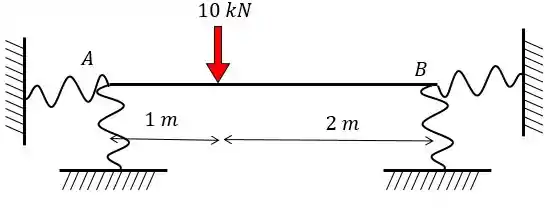
Passo 1
Pessoal, vamos resolver essa questãozinha que tem uma viga em condição hiperestática e possui duas molas, como dito no enunciado. Uhullll
A primeira coisa que a gente tem que lembrar é que vamos retirar as molas e substituir por apoios fixos. Dessa forma a nossa resolução fica mais fácil pois resolvermos um problema hiperestático normal. Depois, lá no final do problema a gente calcula a parcela relativa aos apoios elásticos e soma tudo.
Vamos ver com calma tudo isso, partiu!
Passo 2
Vamos retirar as molas e substituí-las por outros tipos de apoio. Como os apoios estão restritos tanto no eixo vertical quanto no eixo horizontal pelos elásticos então vamos substituir por apoios de segundo gênero. Dessa forma a gente vai ter o seguinte:
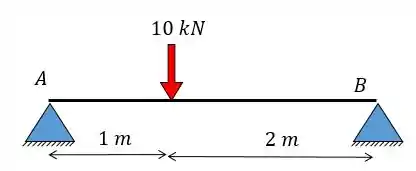
Pronto! Chegamos no nosso problema hiperestático convencional. Agora vamos resolvê-lo normalmente.
Passo 3
Este problema hiperestático possui um grau de hiperestaticidade, então vamos quebrar um vínculo (pode ser qualquer um, eu vou quebrar o apoio ) a gente só precisa lembrar que temos de colocar uma força equivalente. Dessa forma vamos obter:
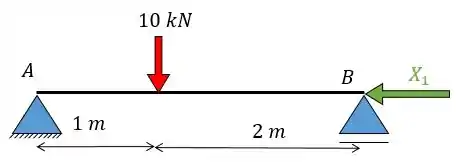
Eis que temos o nosso hiperestático e agora o que temos que fazer é achar o valor desse “indivíduo” escrutável... Para isso vamos dividir o problema em dois sistemas e fazer os seus respectivos diagramas de momento fletor.
Ps: Como, ao dividirmos o problema em dois sistemas, a gente obtém sistemas isostáticos, não vou perder muito tempo fazendo as contas não ok? Só vou mostrar como que fica o resultado para vocês =D
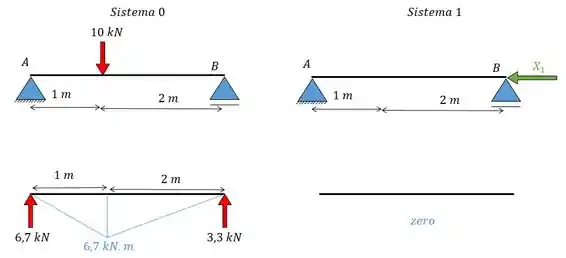
Viram como eu sou bonzinho e além de colocar o diagrama do momento fletor (em azul) ainda coloquei as forças resultantes (em vermelho). Owwnnnnn, que fofis....
Passo 4
Agora a gente tem que lembrar de como calcular o nosso hiperestático . A gente faz isso através da equação do deslocamento que tem a seguinte forma:
Então a gente vai precisar achar a deformação do sistema 0 em relação ao sistema 1 () e do sistema 1 em relação a ele mesmo (). Lembrando que vamos fazer isso com ajuda daquela nossa tabelinha marota. Mas reparem numa coisa, o momento para o caso do sistema 1 é nulo então vamos ter:
Pessoal, achamos os valores de e já podemos substituir na expressão abaixo?
A resposta é não =(
Por que a resposta é não? Porque se fizéssemos isso então a gente não estaria considerando a parte dos apoios elásticos, que até agora ainda não apareceram...
Essa é a diferença dos exercícios com molas. Quando não tem mola, os temos EJCδ são iguais a combinação dos diagramas. Quando tem mola, esses termos são compostos pela combinação dos diagramas + as parcelas referentes às molas. Vamos ver como fica isso.
Passo 5
Para considerarmos a parte relativa aos apoios elásticos nós vamos calcular um novo e um novo , vamos chamá-los de e . Esses novos termos são as deformações de cada apoio elástico e são dados por aquelas equações que vimos na teoria:
Mas nesse caso, não temos molas rotacionais, só molas lineares. Então fica assim:
Ou seja, com as reações de apoio NOS PONTOS ONDE FICAM AS MOLAS, nós vamos poder calcular os valores e . Vamos olhar novamente as reações da nossa viga:
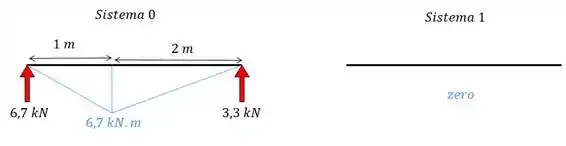
Mas como no sistema 1, as reações de apoio são nulas nos 2 pontos onde temos molas (A e B), então vamos ter:
No caso da combinação , que só usamos o sistema 1, também vai ficar tudo nulo:
Passo 6
Então o que podemos assumir deste exercício?
Como todos os deslocamentos são nulos então de fato o nosso hiperestático é nulo:
Sendo assim, basta substituir na nossa viga e achar as reações normalmente. Lembrando que o nosso hiperestático representa o valor de :
Passo 7
Dessa forma vamos ter:
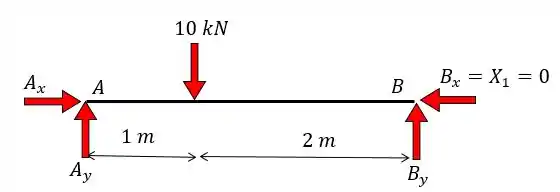
Pelas equações da estáticas vamos achar:
Resposta
Exercício Resolvido #5
Origem do Exercício
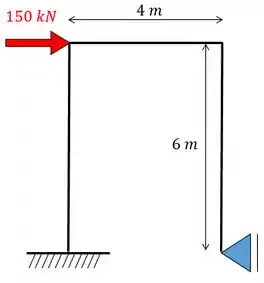
Determine o deslocamento horizontal do ponto C do pórtico dado abaixo.
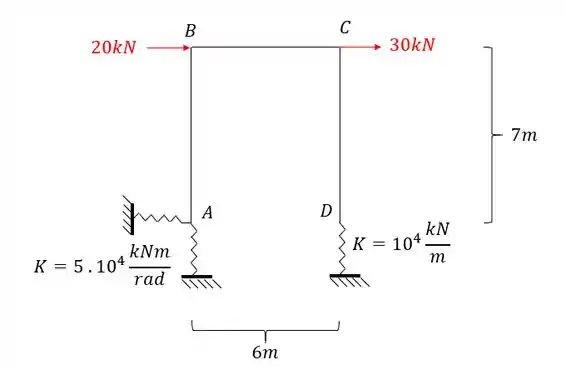
Passo 1
Sabemos que o que devemos fazer é determinar o sistema equivalente que iremos usar na nossa estrutura.
Como só temos molas verticais e horizontais, teremos apenas apoios verticais, sendo assim o nosso sistema será dado por:
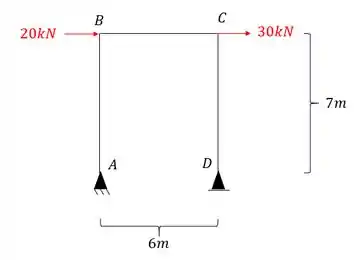
Sabemos que antes de começar a usar qualquer fórmula precisamos garantir logo o nosso diagrama para esse sistema equivalente com o carregamento externo, sendo assim, teremos que o nosso diagrama será:
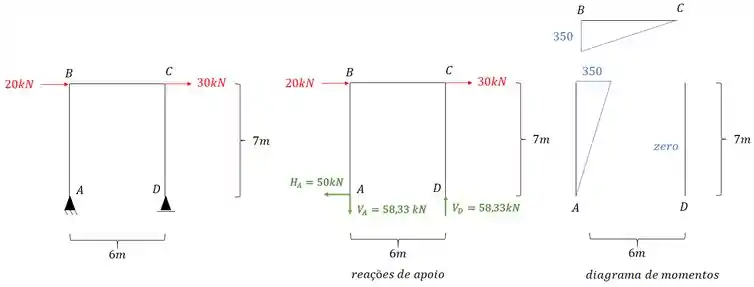
Passo 2
Agora precisamos determinar o deslocamento horizontal do ponto C.
- Deslocamento em C
Para descobrirmos o deslocamento horizontal nele, precisamos por uma carga unitária no ponto em que queremos saber e na direção que queremos saber, dessa maneira teremos que:
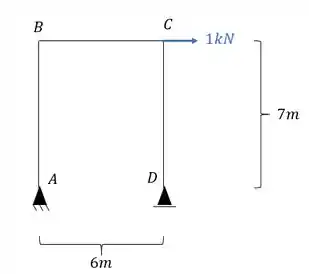
Agora nesse caso iremos ter um diagrama, e nesse caso o diagrama junto com as reações de apoio será dado por:
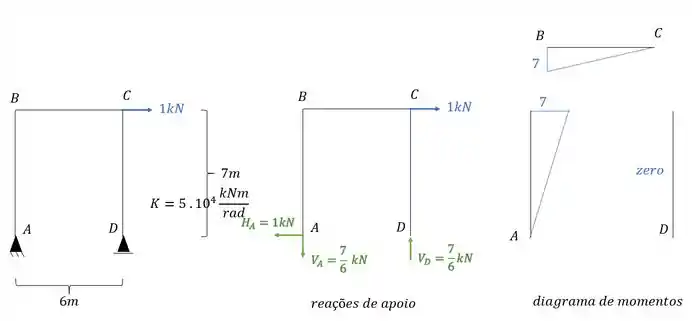
E devemos combinar ele com o diagrama de carregamentos reais que é dado por:
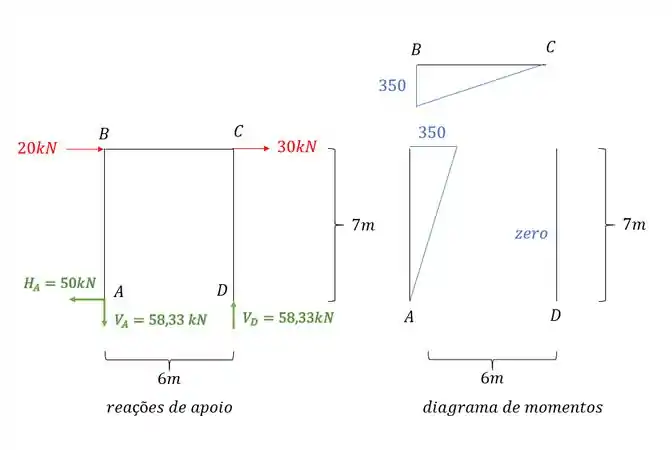
Combinando os diagramas teremos que:
Como temos que:
Substituindo teremos que:
Também temos as reações de apoio que serão dadas por.
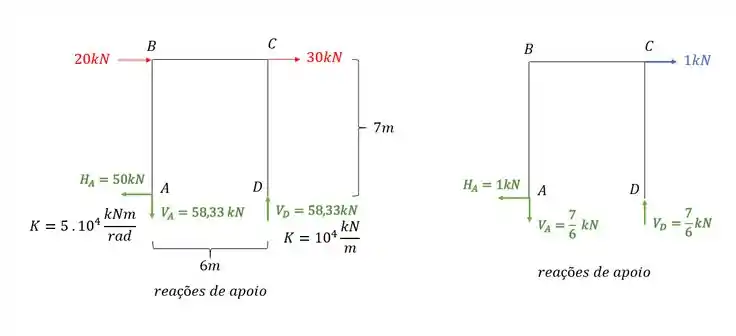
Porque a reação de apoio é importante para nós? Exatamente porque sabemos que a fórmula para determinar a deformação na mola é:
Sabemos que:
E perceba que consideramos a contribuição das duas molas, substituindo o que temos na fórmula teremos que:
Logo a deformação total em C será a soma das duas parcelas dadas por:
Resposta
Exercício Resolvido #6
Origem do Exercício
Determine o deslocamento horizontal do ponto C do pórtico dado abaixo.
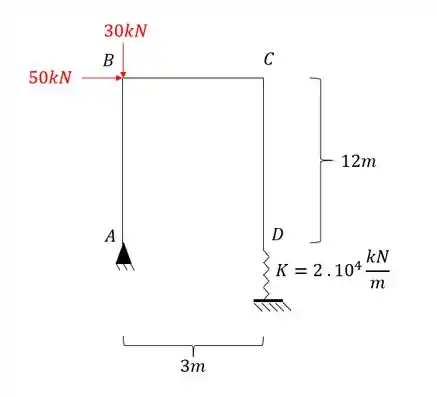
Passo 1
Sabemos que o que devemos fazer é determinar o sistema equivalente que iremos usar na nossa estrutura.
Como só temos uma mola vertical, teremos apenas apoios verticais, sendo assim o nosso sistema será dado por:
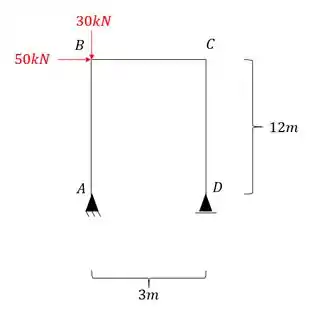
Sabemos que antes de começar a usar qualquer fórmula precisamos garantir logo o nosso diagrama para esse sistema equivalente com o carregamento externo, sendo assim, teremos que o nosso diagrama será:
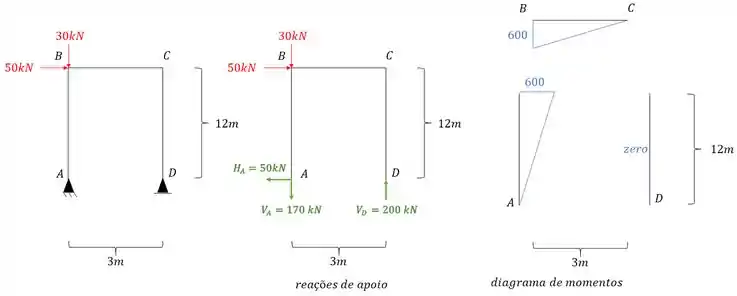
Passo 2
Agora precisamos determinar o deslocamento horizontal do ponto C.
- Deslocamento em C
Para descobrirmos o deslocamento horizontal nele, precisamos por uma carga unitária no ponto em que queremos saber e na direção que queremos saber, dessa maneira teremos que:
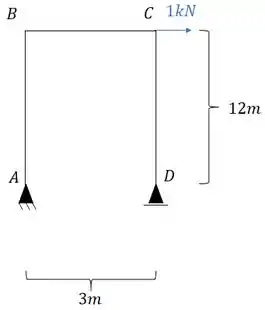
Agora nesse caso iremos ter um diagrama, e nesse caso o diagrama junto com as reações de apoio será dado por:
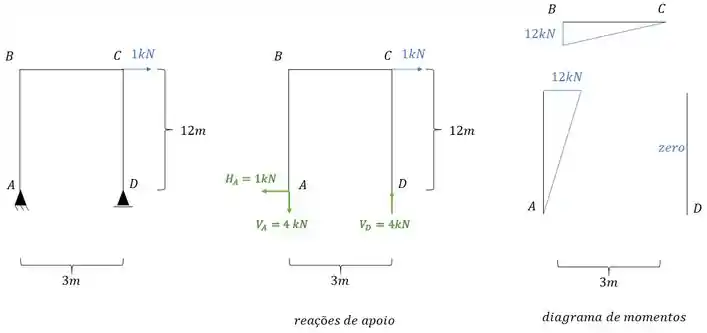
E devemos combinar ele com o diagrama de carregamentos reais que é dado por:
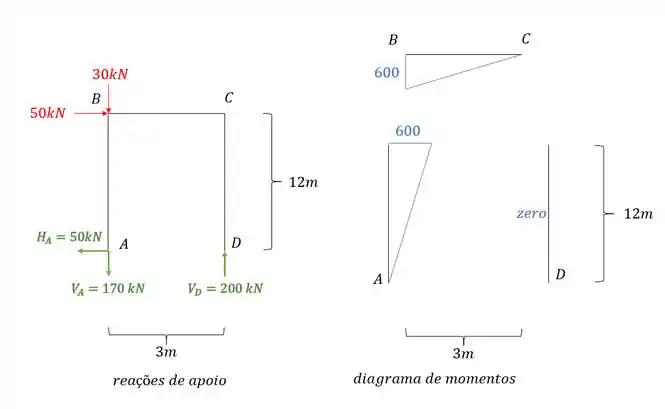
Combinando os diagramas teremos que:
Como temos que:
Substituindo teremos que:
Também temos as reações de apoio que serão dadas por.
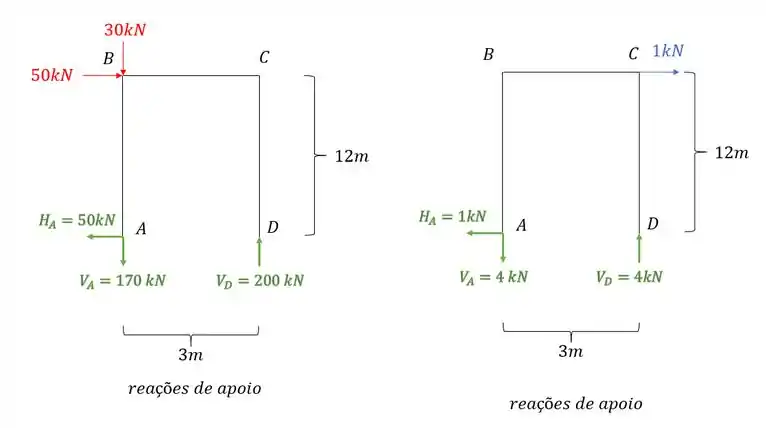
Porque a reação de apoio é importante para nós? Exatamente porque sabemos que a fórmula para determinar a deformação na mola é:
Sabemos que:
Substituindo o que temos na fórmula teremos que:
Logo a deformação total em C será a soma das duas parcelas dadas por:
Resposta
Exercício Resolvido #7
Origem do Exercício
Determine o diagrama de momentos fletores do pórtico abaixo.
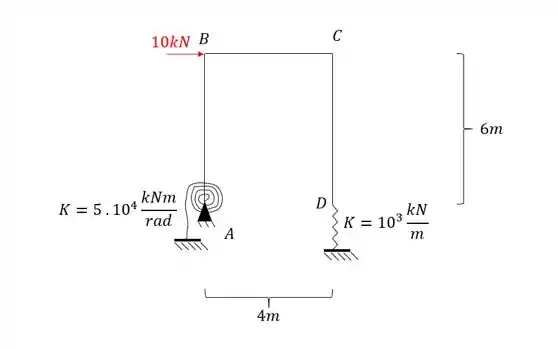
Passo 1
Antes de determinar qualquer coisa precisamos antes determinar o sistema equivalente que iremos usar na nossa estrutura.
No apoio esquerdo temos um apoio do segundo gênero, mas uma mola do tipo engaste elástico, sendo assim, podemos representar como um apoio do terceiro gênero. Em contra partida, o apoio da direita é apenas uma mola vertical, sendo dessa maneira apenas um apoio do primeiro gênero. Teremos assim que a nossa estrutura equivalente será:
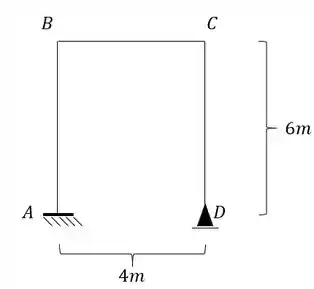
Perceba que nosso sistema equivalente é hiperestático, com 4 incógnitas e 3 equações. Com isso precisamos quebrar pelo menos um vínculo para termos um sistema isostático e dessa maneira resolvermos o seguinte sistema:
Passo 2
Quebrando o vínculo de momento do apoio engastado temos que:
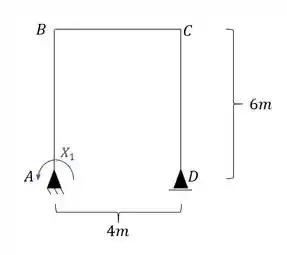
Sabemos que antes de começar a usar qualquer fórmula precisamos garantir logo o nosso diagrama para esse sistema equivalente com o carregamento externo, sendo assim, teremos que o nosso diagrama será:
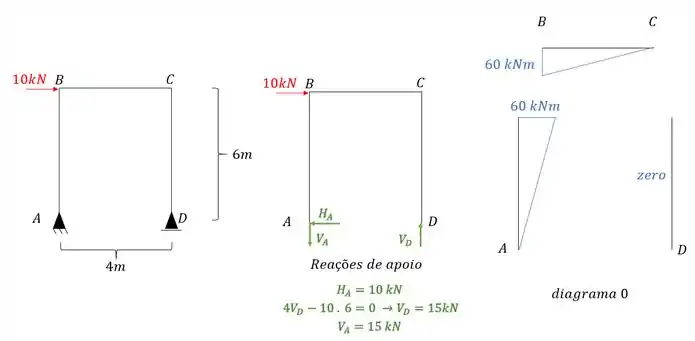
Passo 3
Da mesma maneira precisamos determinar o nosso diagrama considerando o nosso hiperestático igual a 1, sendo assim teremos que:
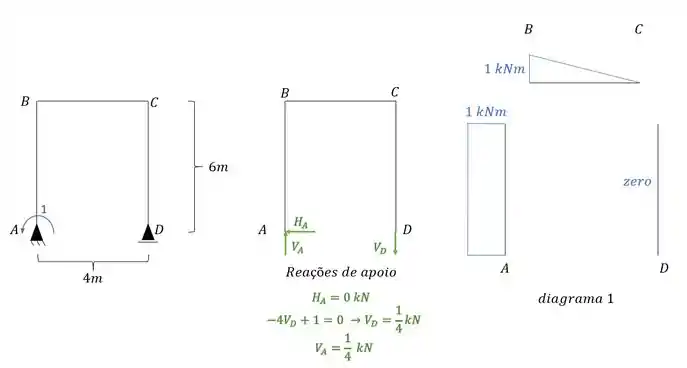
Passo 4
Agora precisamos determinar cada uma das nossas deformações, vamos começar pela deformação .
-
Sabemos que como temos mola na nossa estrutura deveremos tomar alguns cuidados, mas em suma, para nossa deformação devemos ter as seguintes parcelas:
- Combinação do diagrama zero com o diagrama 1
- Combinação da reação da mola em A no sistema zero e a reação da mola em A no sistema com a carga unitária (lembrando que que a mola em A é um engaste elástico)
- Combinação da reação da mola em D no sistema zero e a reação da mola em D no sistema com a carga unitária (lembrando que que a mola em D é uma mola vertical).
-
Sabemos que como temos mola na nossa estrutura devemos tomar alguns cuidados, mas em suma, para nossa deformação devemos ter as seguintes parcelas:
- Combinação do diagrama 1 com o diagrama 1
- Combinação da reação da mola em A no sistema com a carga unitária e a reação da mola em A no sistema com a carga unitária (lembrando que que a mola em A é um engaste elástico)
- Combinação da reação da mola em D no sistema com a carga unitária e a reação da mola em D no sistema com a carga unitária (lembrando que que a mola em D é uma mola vertical).
Sabendo disso vamos começar pela combinação de diagramas:
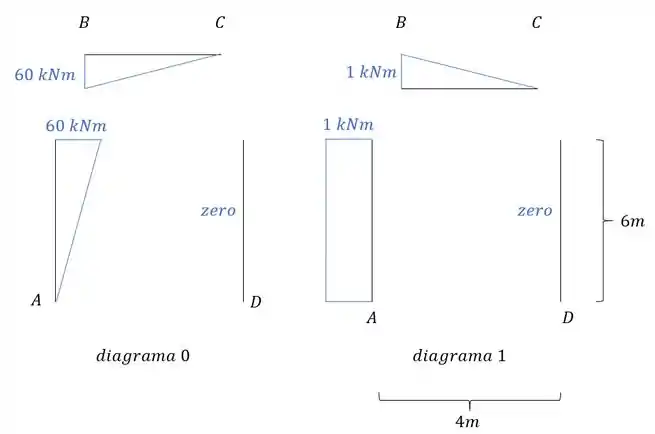
Precisamos fazer a combinação da mola que temos em A, e assim teremos que como é um engaste elástico a nossa fórmula será:
Olhando as reações de apoio teremos que:

Assim teremos que:
E por fim fazemos a combinação para determinação da contribuição da mola em B, que é uma mola vertical que calcularemos pela equação:
Olhando as nossas reações de apoio teremos que:

Substituindo teremos que:
Juntando tudo teremos que:
Passo 5
Agora precisamos determinar a deformação .
Sabendo disso vamos começar pela combinação de diagramas:
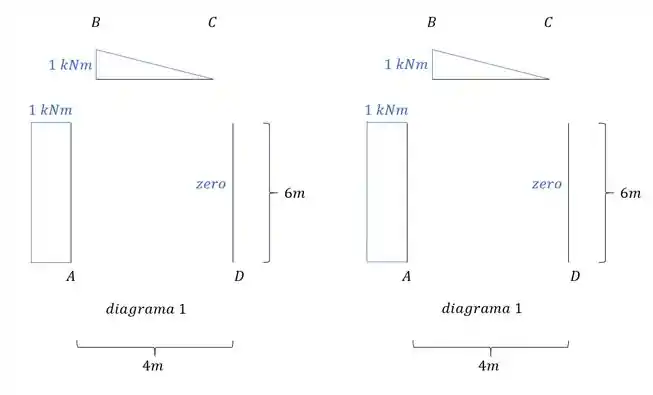
Precisamos fazer a combinação da mola que temos em A, e assim teremos que como é um engaste elástico a nossa fórmula será:
Olhando as reações de apoio teremos que:
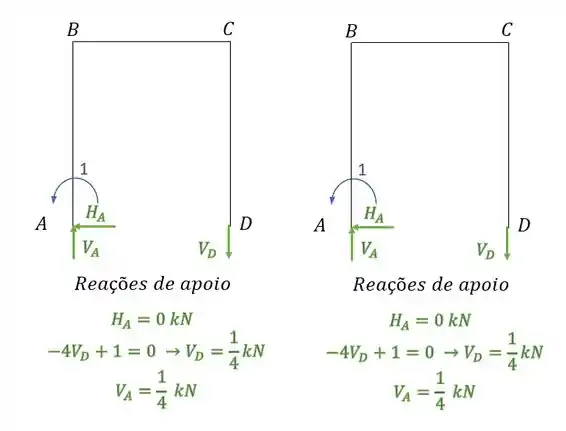
Assim teremos que:
E por fim fazemos a combinação para determinação da contribuição da mola em B, que é uma mola vertical que calcularemos pela equação:
Olhando as nossas reações de apoio teremos que:
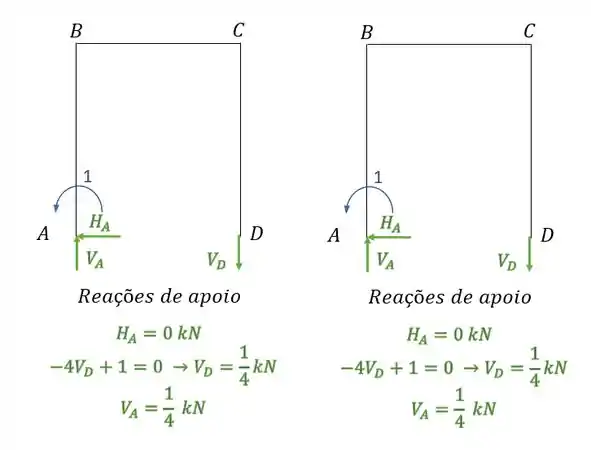
Substituindo teremos que:
Juntando tudo teremos que:
Passo 5
Agora substituímos no nosso sistema que é dado por:
Substituindo teremos que:
Passo 6
Para determinação dos momentos devemos usar:
Em que i é o ponto que estamos determinando o nosso momento, sendo assim teremos que:
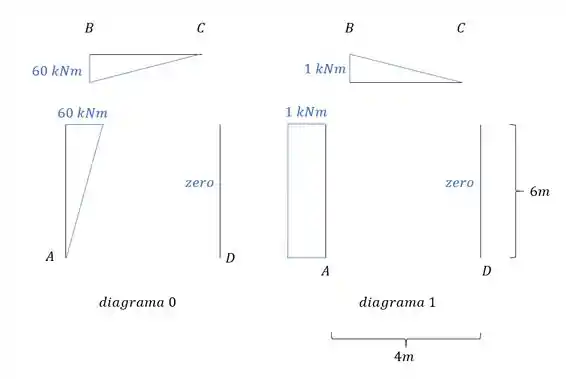
Substituindo vamos ter que:
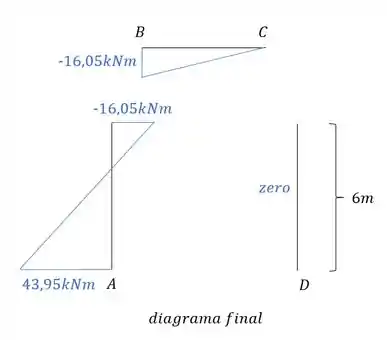
Montando esse diagrama vamos ter que:
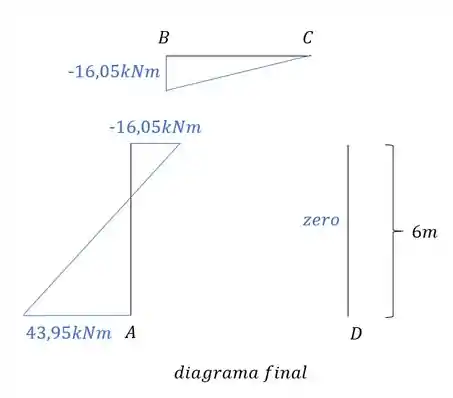
Resposta
Exercício Resolvido #8
Elaboração própria
Determine as reações de apoio do pórtico abaixo.
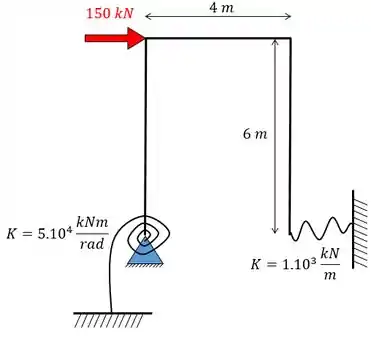
Passo 1
Fala, galerinha!!! Esse problema pede para acharmos as reações de apoio e para isso é importante a gente perceber que existem dois apoios elásticos e que se trata de uma estrutura hiperestática.
Então a primeira coisa que vamos fazer é trocar os apoios elásticos por apoios simples. Depois nós vamos trabalhar apenas com a estrutura hiperestática, quebrando os apoios e aplicando as forças (hiperestáticos) correspondentes.
Por fim vamos aplicar o conceito dos deslocamentos para achar o hiperestático e o deslocamento pedido!
Passo 2
Vamos achar a estrutura correspondente, sem os apoios elásticos. A mola rotacional irá se transformar num engaste e a mola linear num apoio de primeiro gênero.
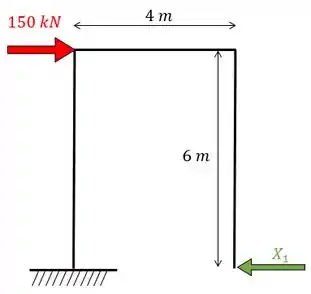
Perceba que temos uma estrutura hiperestática com grau hiperestático igual a 1. Então vamos quebrar um dos apoios de forma a obter um sistema isostático:
E como temos um hiperestático vamos dividir em 2 sistemas:
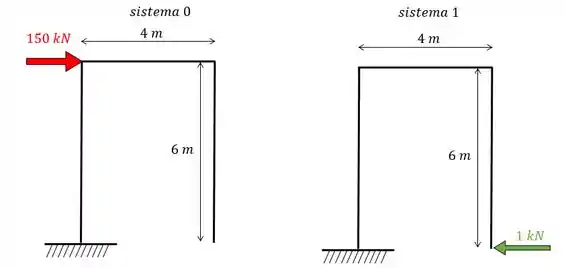
Passo 3
Beleza, agora vamos como vão ficar as nossas equações do deslocamento. Se não tivéssemos as molas a nossa equação seria da seguinte forma:
Mas a gente tem dois apoios elásticos que também irão se deslocar, então temos de aplicar o deslocamento referente aos apoios elásticos. Isso acontece da forma:
Ou seja, para cada e nós vamos ter na verdade três deslocamentos: o do sistema hiperestático, o da mola linear e o da mola rotacional. Assim vamos ter:
Onde:
Então para resolver nosso sistema nós vamos ter que achar esses 6 deltas ().
Passo 4
Vamos achar primeiro os deltas da estrutura hiperestática, e .
Para isso a gente precisa desenhar o diagrama do momento fletor para cada sistema, obtendo:
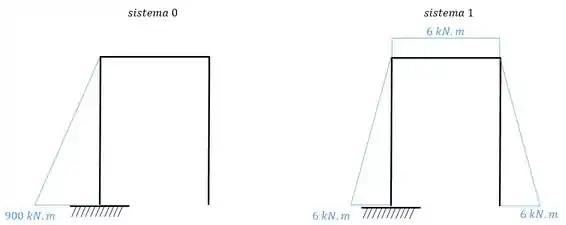
Agora vamos fazer as combinações, vamos começar com o deslocamento que, por ter duas barras com momento fletor nulo, nos fornece apenas a combinação de dois triângulos. Assim, vamos ter:
Substituindo os valores.
Esse já foi! Agora vamos para . Dessa vez vamos ter a combinação de (2 triângulos + 2 retângulos + 2 triângulos)
Substituindo os valores.
Para os sistemas hiperestáticos já acabamos agora vamos ver os deslocamentos referentes às molas.
Passo 5
No caso das molas nós vamos ter a linear e a rotacional sendo que para cada uma delas vamos aplicar as duas combinações dos sistemas e . Dessa forma podemos começar pela mola linear. Agora o que importa para nós não é o diagrama de momentos fletores mas sim as reações de cada apoio:
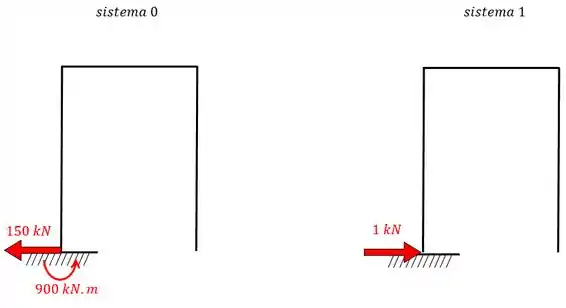
Aplicando a equação da mola linear vamos ter:
Substituindo os valores vamos obter:
E vamos fazer a mesma coisa para o sistema 11:
Substituindo os valores vamos obter:
Passo 6
Agora para a mola rotacional. No caso das molas lineares a gente utiliza as forças e para molas rotacionais utilizamos o momento. Lembrando do diagrama de resultantes:
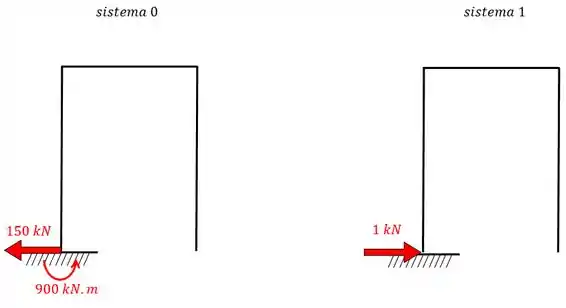
Aplicando o conceito:
Aqui não precisamos nem substituir porque no sistema 1 não há momento, logo . Dessa forma
Passo 7
Agora que achamos os 6 deltas vamos somar todos:
Obtendo:
Agora é só aplicar na equação real:
Passo 8
Agora é só achar o resto das forças:
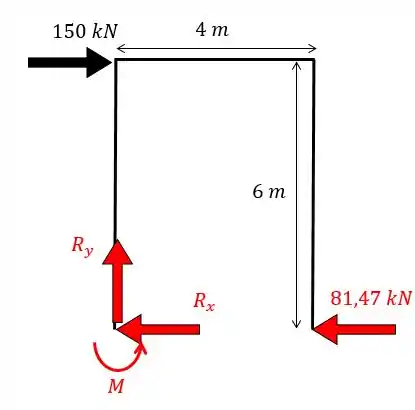
Aplicando as equações da estática vamos obter:
Resposta