Deslocamento em Estruturas Isostáticas – Método das Tabelas
Produzido por Pablo RicardoTeoria
Tem um jeito mais rápido de calcular deslocamento nas estruturas?
Opa, tem sim! Existe um método que nos ajuda muito... com uma fórmula só ele calcula deslocamentos em estruturas que tem momentos de inércias diferentes (porém constantes) em diferentes pontos!
Esse método ainda nos dá uma tabela que nos ajuda a calcular tudo de maneira mais simples, como se fosse mágica. O método das tabelas está para deslocamentos como a seção de Richter está para treliças, ou seja, é um método que acelera os cálculos de deslocamentos usando uma tabela.
Á fórmula de cara parece meio feinha, porque ela é assim:
Feia né? Mas vamos simplificar as coisas que ela vai ficar bem mais simples.
Esse é o nosso velho conhecido módulo de elasticidade, então quanto a ele podemos ficar bem tranquilos porque esse não mudou.
- Coluna vertical
- Coluna horizontal
- Coluna horizontal + coluna vertical
- L’
- O sinal
- Barra 1
- Barra 2
- Barra 3
Esse cara é novo, mas ele é bem legal porque ele facilita a nossa vida. Ele é o que a gente chama de Momento de inércia de comparação, e a utilidade dele é permitir que a gente facilite as nossas contas. Por exemplo, imagine que eu tenha um pórtico com os seguintes momentos de inércia:
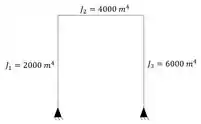
Você percebe que é meio complicado trabalhar com um pórtico com tantos momentos de inércia diferentes. Então, podemos fazer o seguinte: podemos adotar um momento de inércia de comparação, que geralmente fazemos igual ao menor momento de inercia do pórtico, com isso teríamos que:
Com isso podemos escrever o nosso pórtico como
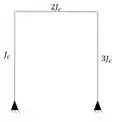
E porque fazemos o que fizemos com o pórtico anterior? De simplificar tudo para ? Exatamente para facilitarmos o nosso cálculo dessa divisão. O termo de cima sempre vai ser . O termo de baixo vai variar para cada barra (no nosso exemplo anterior seria , e como sabemos que é um somatório que vem antes, já sabemos que teremos que fazer uma relação e uma integral para cada uma das barras. Perceba que se analisarmos pórticos com o mesmo momento de inercia em todas as barras, esse fator sempre vai ser 1, e então não vamos precisar nos preocupar com ele.
Esse termo vai ser o que a gente vai usar a nossa tabelinha de momentos. Eu já vou mostrar pra vocês a tabelinha, mas é importante lembrar que pra gente, representa sempre os momentos fletores que de fato ocorrem na nossa peça, e seus diagramas. Enquanto que representa os momentos fletores que ocorrem na nossa peça devido a uma carga unitária colocada no ponto e na direção que queremos saber o deslocamento. Por exemplo, se quisermos saber o deslocamento horizontal em um certo ponto A, colocamos uma carga unitária, no ponto A, na direção horizontal, e aí calculamos os momentos fletores, beleza?
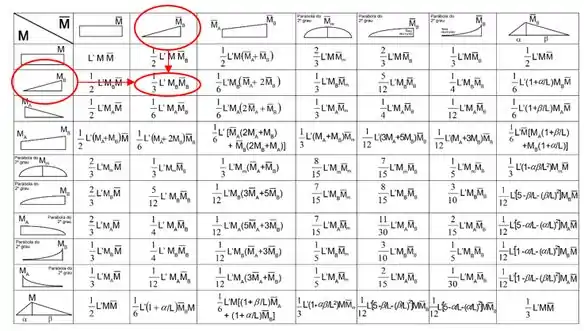
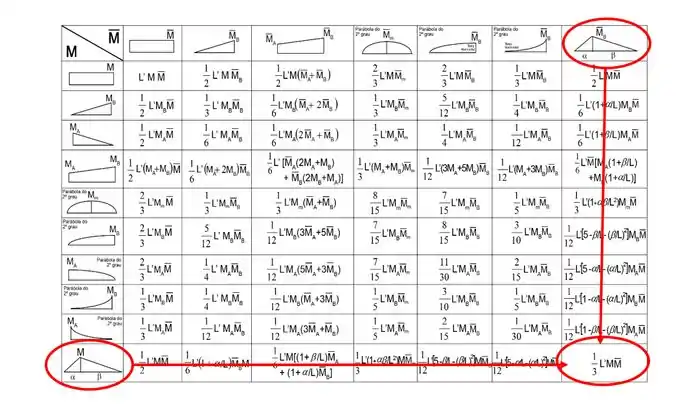
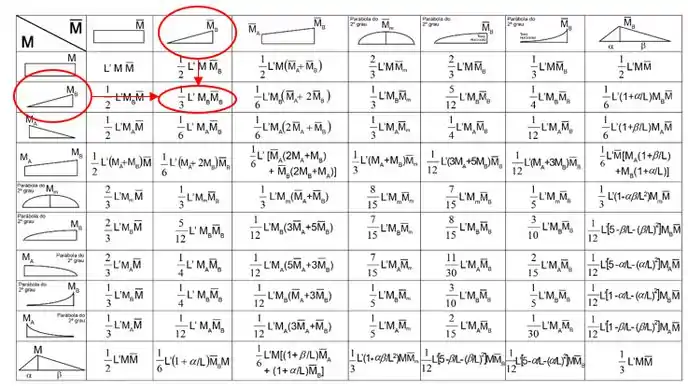
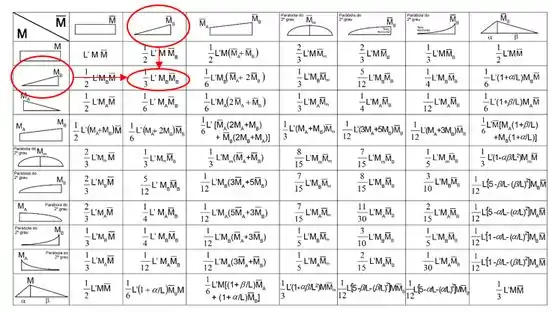
Mas e a tabela? A nossa tabela é a seguinte:
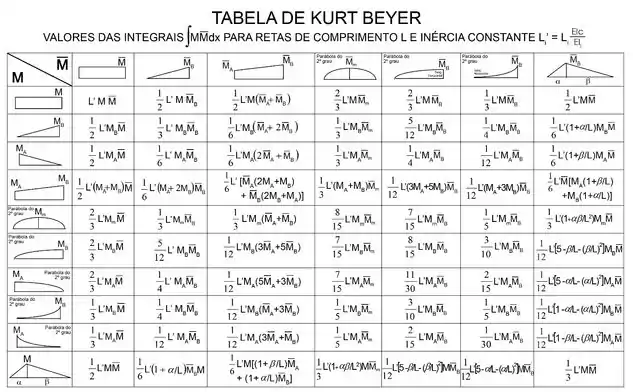
E tem algumas coisas importantes que precisamos saber dessa tabela antes de sair usando ela.
Você pode ver que a coluna vertical representa o formato do diagrama de momento reais que agem na barra que estamos analisando.
Representa o formato do diagrama de momentos virtuais que agem na mesma barra que estávamos analisando pra coluna vertical.
Combinando o que achamos pra coluna vertical com o que achamos para a coluna horizontal, encontramos uma fórmula que entra no lugar do termo , tornando o cálculo muito mais simples.
É MUITO IMPORTANTE tomar cuidado com esse termo, sempre que todas as inercias de todas as barras forem iguais, o comprimento que vamos usar vai ser o próprio comprimento da barra, mas quando for diferente, usaremos uma variação desse valor de acordo com a inércia, que é dada pela seguinte fórmula.
E vai ser o valor de L’ que vai entrar na formula.
É bem importante entender como funciona o sinal, é bem fácil, mas precisamos tomar muito cuidado. Ele funciona da seguinte maneira:
Sempre que combinarmos momentos que estejam do mesmo lado, vai ser positivo. E sempre que combinarmos momentos que estejam em lado opostos vai ser negativo.
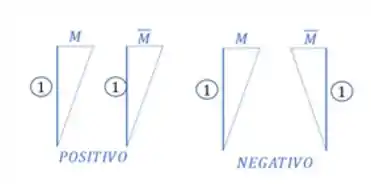
Mas agora que sabemos isso tudo, vamos fazer um passo a passo pra entender bem o que temos que fazer.
Exemplinho bem tranquilo
Imagine que queremos determinar o deslocamento horizontal do ponto D do seguinte pórtico dado aqui em baixo com . E todas as barras possuem inercias iguais.
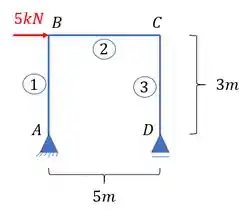
Passo 1
A primeiro coisa que devemos fazer é verificar a inércia. Como foi dito que todas as inercias são iguais, então podemos dizer que:
Se é tudo igual, isso implica que:
Que simplifica a nossa fórmula para
Passo 2
A segunda coisa que precisamos fazer é determinar o diagrama de momentos devido a carga que age na nossa estrutura, e o diagrama fica sendo:
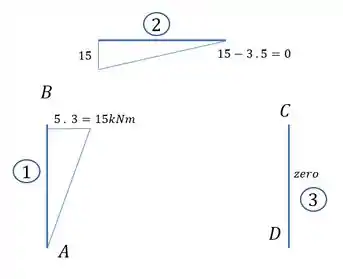
E perceba que fizemos bem separadinho pra ficar fácil de entender.
Passo 3
Aplicamos a carga unitária no ponto em que queremos saber o deslocamento, e determinamos o diagrama de momentos fletores causados por essa carga unitária.
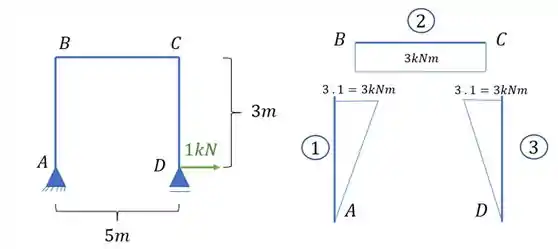
Passo 4
Determinação das combinações para cada uma das barras.
Primeiro temos as barras com os seus momentos.
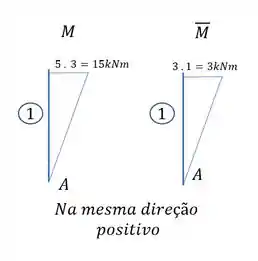
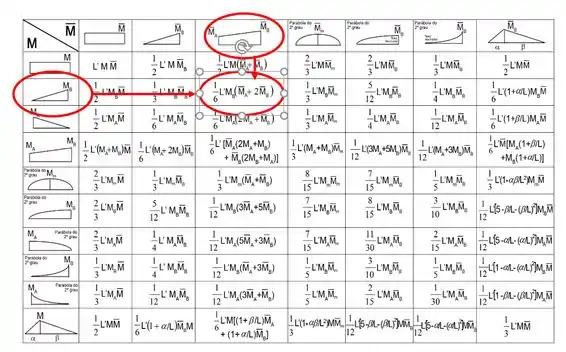
Usando a tabela temos que:

E a fórmula será a combinação desses dois gráficos.
E por fim verificamos se o comprimento da barra se manterá igual
Que para a barra 1 será igual a 3m.
Substituindo na fórmula teremos que
Primeiro temos as barras com os seus momentos.
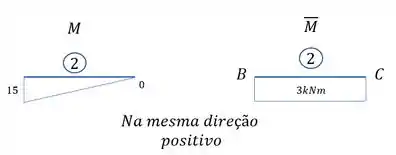
Usando a tabela temos que:
E por fim verificamos se o comprimento da barra se manterá igual
Que para a barra 2 será igual a 5m.
Substituindo na fórmula teremos que
Primeiro temos as barras com os seus momentos.
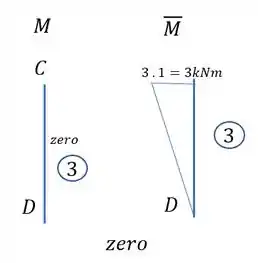
Substituindo na fórmula teremos que
Passo 5
Cálculo da deformação total
Como sabemos que:
Substituindo teremos que
Ufa, em fim terminamos, agora que ficou bem simples entender o funcionamento dos deslocamentos nas estruturas isostáticas pelo método das tabelas, bora fazer exercício pra isso ficar ainda mais tranquilo. Vamos partir pros exercícios.
Exemplinho bem tranquilo
Passo 1
Passo 2
Passo 3
Passo 4
Passo 5
Exercícios Resolvidos
Exercício Resolvido #1
José Carlos Süssekind, Curso de análise estrutural, Deformação em estruturas método das forças, 4ºed.RJ:LTC,1980,(pagina),(número do exercício)
Calcule o deslocamento horizontal do ponto C do pórtico dado abaixo usando o método das tabelas.
Use para todas as barras do pórtico.
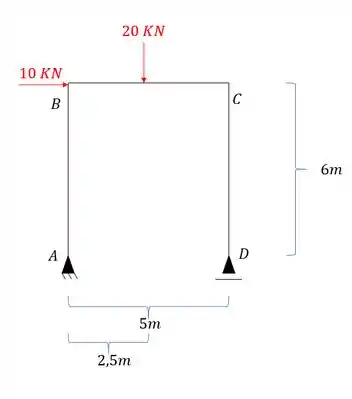
Passo 1
Como vimos na teoria temos um passo a passos bem legal que podemos ir seguindo para determinarmos o deslocamento do nosso ponto.
A primeira coisa que devemos fazer é verificar a inércia. Como foi dito que todas as inercias são iguais, então podemos dizer que:
Se é tudo igual, isso implica que:
Que simplifica a nossa fórmula para
Passo 2
A segunda coisa que precisamos fazer é determinar o diagrama de momentos devido a carga que age na nossa estrutura, e o diagrama fica sendo:
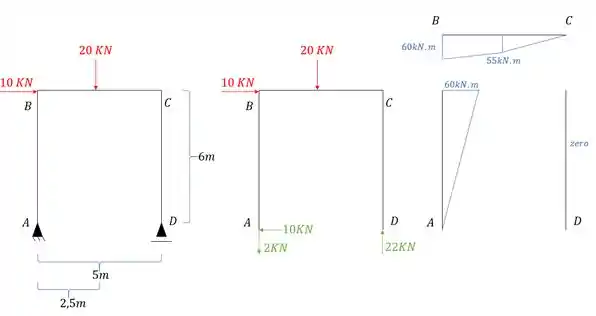
E perceba que fizemos bem separadinho pra ficar fácil de entender.
Passo 3
Aplicamos a carga unitária no ponto em que queremos saber o deslocamento, na direção que queremos saber o deslocamento, e determinamos o diagrama de momentos fletores causados por essa carga unitária.
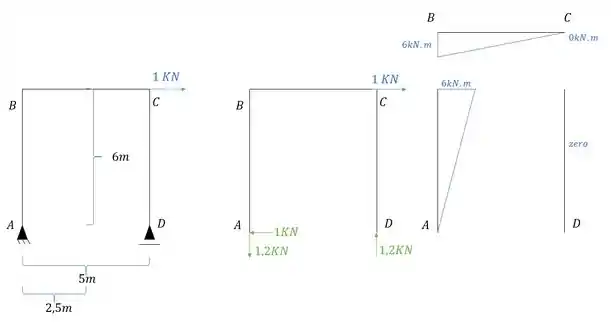
Passo 4
Determinação das combinações para cada uma das barras.
- Barra 1
- Barra 2
- Região com trapézios
- Região com triângulos
- Barra 3
Primeiro temos as barras com os seus momentos.
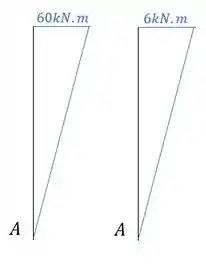
Como estão na mesma direção sabemos que é positivo.
Usando a tabela temos que:

E a fórmula será a combinação desses dois gráficos.
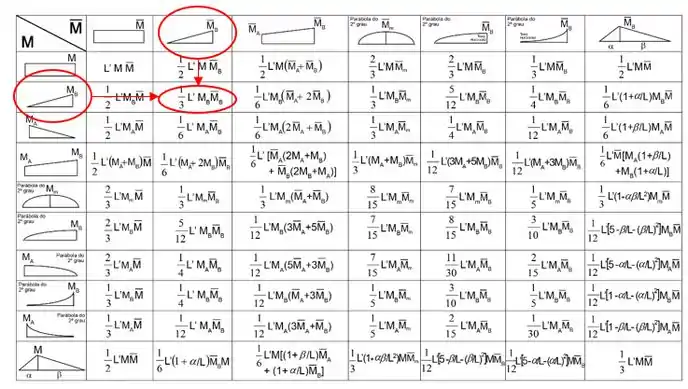
E por fim verificamos se o comprimento da barra se manterá igual
Que para a barra 1 será igual a 6m.
Substituindo na fórmula teremos que
Primeiro temos as barras com os seus momentos.
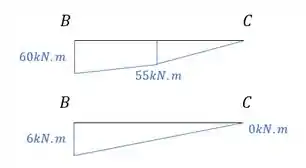
Perceba que a primeira barra, do caso real, possui duas regiões diferentes. Quando isso acontece devemos compatibilizar as regiões da seguinte maneira.
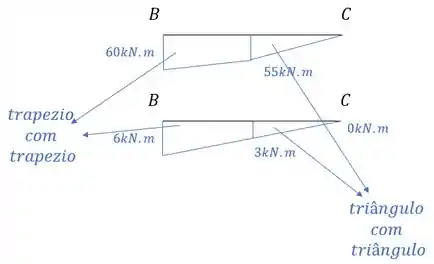
Usando a tabela temos que:
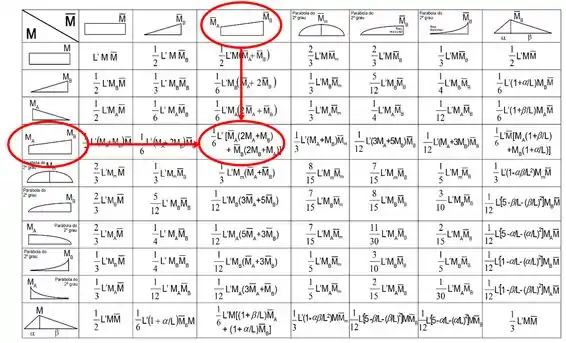
E por fim verificamos se o comprimento da barra se manterá igual
Que para a barra 2 será igual a 2,5m por estarmos combinando diagramas na metade da barra.
Substituindo na fórmula teremos que
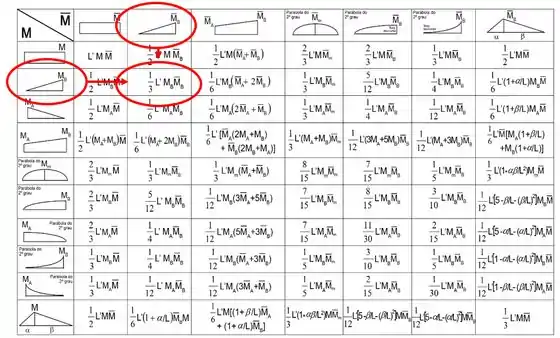
Substituindo na fórmula teremos que
Como ambas as barras são zero podemos desprezar essa parte, mas já sabemos que o valor é zero
Passo 5
Cálculo da deformação total
Como sabemos que:
Substituindo teremos que
Resposta
Exercício Resolvido #2
José Carlos Süssekind, Curso de análise estrutural, Deformação em estruturas método das forças, 4ºed.RJ:LTC,1980,(pagina),(número do exercício)
Calcule o deslocamento Vertical do ponto D do pórtico dado abaixo usando o método das tabelas.
Use para todas as barras do pórtico.
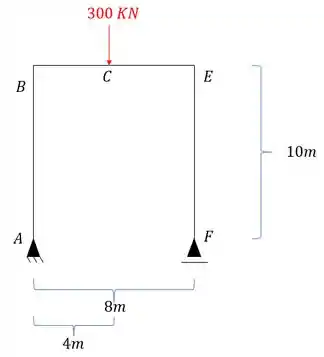
Passo 1
Como vimos na teoria temos um passo a passos bem legal que podemos ir seguindo para determinarmos o deslocamento do nosso ponto.
A primeira coisa que devemos fazer é verificar a inércia. Como foi dito que todas as inercias são iguais, então podemos dizer que:
Se é tudo igual, isso implica que:
Que simplifica a nossa fórmula para
Passo 2
A segunda coisa que precisamos fazer é determinar o diagrama de momentos devido a carga que age na nossa estrutura, e o diagrama fica sendo:
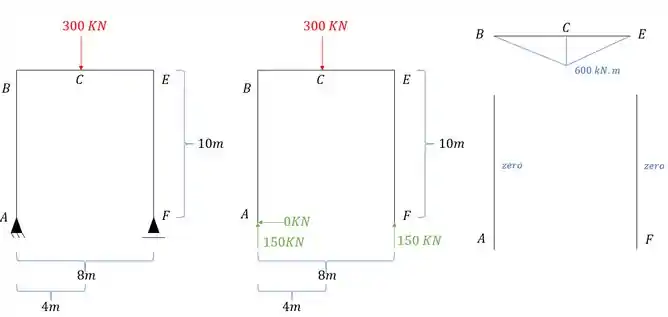
E perceba que fizemos bem separadinho pra ficar fácil de entender.
Passo 3
Aplicamos a carga unitária no ponto em que queremos saber o deslocamento, na direção que queremos saber o deslocamento, e determinamos o diagrama de momentos fletores causados por essa carga unitária.
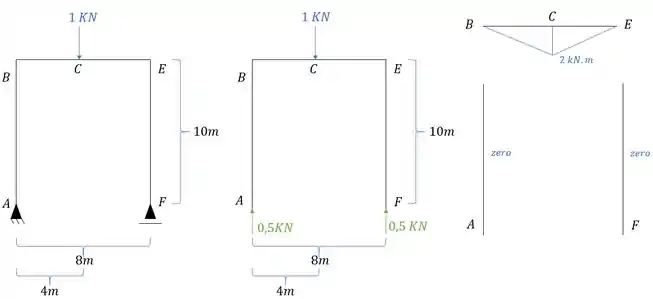
Passo 4
Determinação das combinações para cada uma das barras.
- Barra 1 e 3
- Barra 2
Como ambas as barras são zero podemos desprezar essa parte, mas já sabemos que o valor é zero
Primeiro temos as barras com os seus momentos.
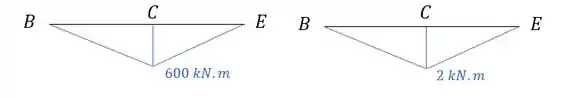
Como estão na mesma direção sabemos que é positivo.
Usando a tabela temos que:
E a fórmula será a combinação desses dois gráficos.
E por fim verificamos se o comprimento da barra se manterá igual
Que para a barra 2 será igual a 8m.
Substituindo na fórmula teremos que
Passo 5
Cálculo da deformação total
Como sabemos que:
Substituindo teremos que
Resposta
Exercício Resolvido #3
José Carlos Süssekind, Curso de análise estrutural, Deformação em estruturas método das forças, 4ºed.RJ:LTC,1980, (Adaptado)
Calcule o deslocamento vertical do ponto médio do pórtico dado abaixo usando o método das tabelas.
Use para todas as barras do pórtico.
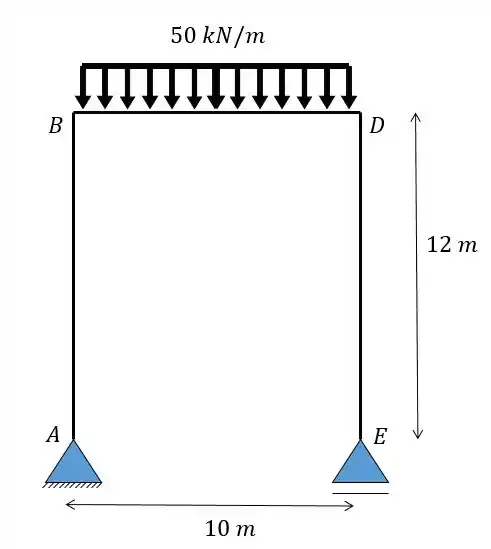
Passo 1
Como vimos na teoria temos um passo a passos bem legal que podemos ir seguindo para determinarmos o deslocamento do nosso ponto.
A primeira coisa que devemos fazer é verificar a inércia. Como foi dito que todas as inercias são iguais, então podemos dizer que:
Se é tudo igual, isso implica que:
Como a nossa equação é dada por:
Então podemos simplificar a nossa fórmula para
Passo 2
A segunda coisa que precisamos fazer é determinar o diagrama de momentos devido a carga que age na nossa estrutura, fazendo isso vamos ter o seguinte diagrama para a barra :
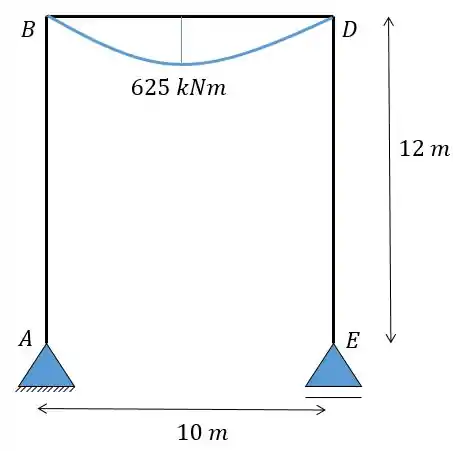
Como só existem forças verticais então não há momento fletor nas outras barras.
Passo 3
Aplicamos a carga unitária no ponto em que queremos saber o deslocamento, na direção que queremos saber o deslocamento.
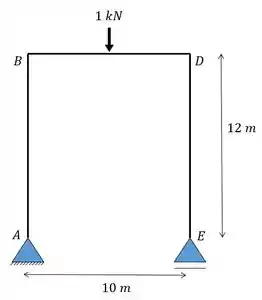
Depois determinamos o diagrama de momentos fletores causados por essa carga unitária.
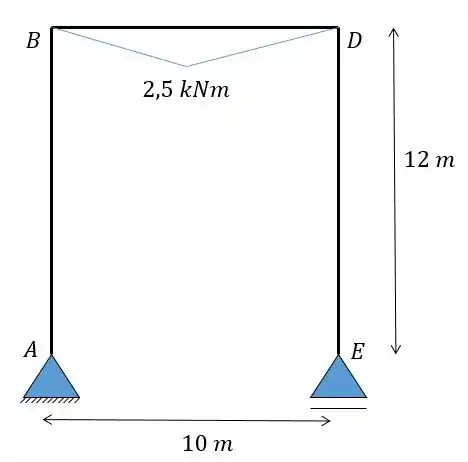
Passo 4
Determinação das combinações para cada uma das barras.
- Barra e
- Barra
Como ambas as barras são zero podemos desprezar essa parte, mas já sabemos que o valor é zero
Primeiro temos as barras com os seus momentos.
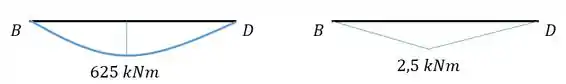
Como estão na mesma direção sabemos que é positivo.
Usando a tabela temos que:
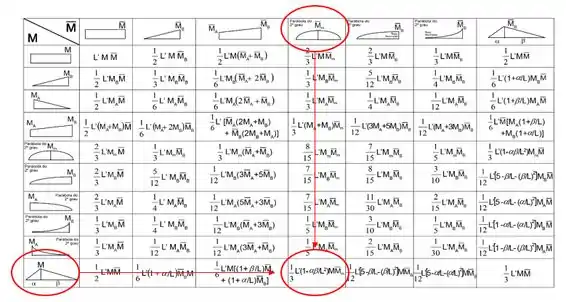
A fórmula será a combinação desses dois gráficos , já já vamos fazer isso mas antes vamos verificar se o comprimento da barra se manterá igual:
Que para a barra será igual a .
Substituindo na fórmula teremos que
Passo 5
Cálculo da deformação total
Como sabemos que:
Substituindo teremos que
Resposta
Exercício Resolvido #4
José Carlos Süssekind, Curso de análise estrutural, Deformação em estruturas método das forças, 4ºed.RJ:LTC,1980,(pagina),(número do exercício)
Calcule o deslocamento Vertical do ponto D da viga dada abaixo usando o método das tabelas.
Use para todos os trechos da viga.
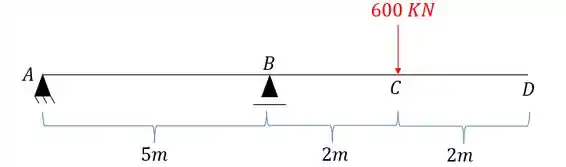
Passo 1
Como vimos na teoria temos um passo a passos bem legal que podemos ir seguindo para determinarmos o deslocamento do nosso ponto.
A primeira coisa que devemos fazer é verificar a inércia. Como foi dito que todas as inercias são iguais, então podemos dizer que:
Se é tudo igual, isso implica que:
Que simplifica a nossa fórmula para
Passo 2
A segunda coisa que precisamos fazer é determinar o diagrama de momentos devido a carga que age na nossa estrutura, e o diagrama fica sendo:
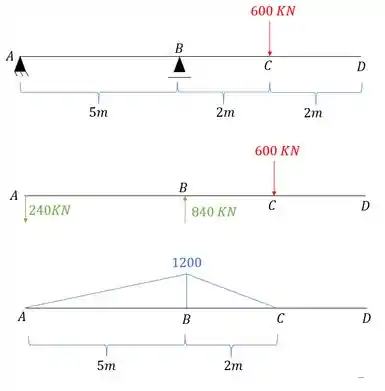
E perceba que fizemos bem separadinho pra ficar fácil de entender.
Passo 3
Aplicamos a carga unitária no ponto em que queremos saber o deslocamento, na direção que queremos saber o deslocamento, e determinamos o diagrama de momentos fletores causados por essa carga unitária.
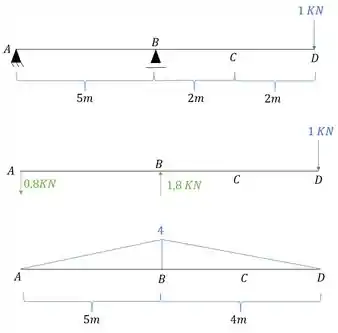
Passo 4
Determinação das combinações para cada uma das barras.
- Trecho AB
- Trecho BC
- Região com trapézio-triangulo
- Região CD
Primeiro temos as barras com os seus momentos.
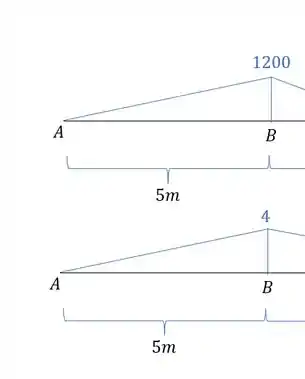
Como estão na mesma direção sabemos que é positivo.
Usando a tabela temos que:

E a fórmula será a combinação desses dois gráficos.
E por fim verificamos se o comprimento da barra se manterá igual
Que para a barra 1 será igual a 5m.
Substituindo na fórmula teremos que
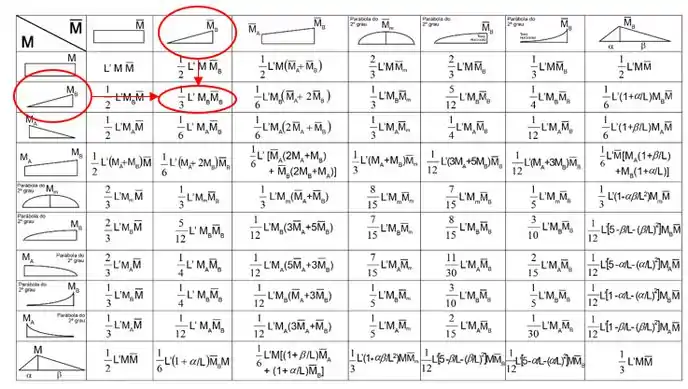
Primeiro temos as barras com os seus momentos.
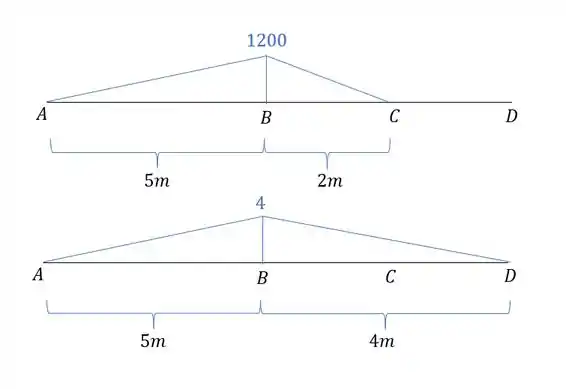
Perceba que a primeira barra, do caso real, para o trecho BC, possui duas regiões diferentes. Uma triangular e uma zero. Enquanto a barra com carregamento virtual é triangular, com isso basta combinas a região certa.
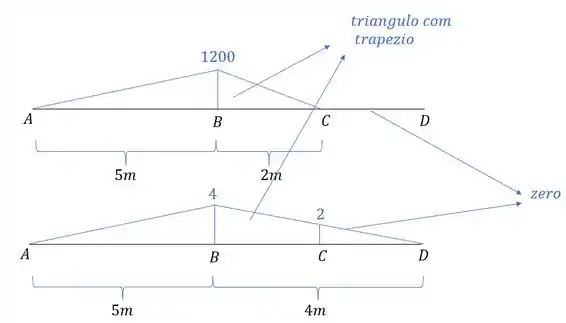
Usando a tabela temos que:
E por fim verificamos se o comprimento da barra se manterá igual
Que para a barra 2 será igual a 2m por estarmos combinando diagramas na metade da barra.
Substituindo na fórmula teremos que
Como ambas as barras são zero podemos desprezar essa parte, mas já sabemos que o valor é zero
Passo 5
Cálculo da deformação total
Como sabemos que:
Substituindo teremos que
Resposta
Exercício Resolvido #5
José Carlos Süssekind, Curso de análise estrutural, Deformação em estruturas método das forças, 4ºed.RJ:LTC,1980,(pagina),(número do exercício)
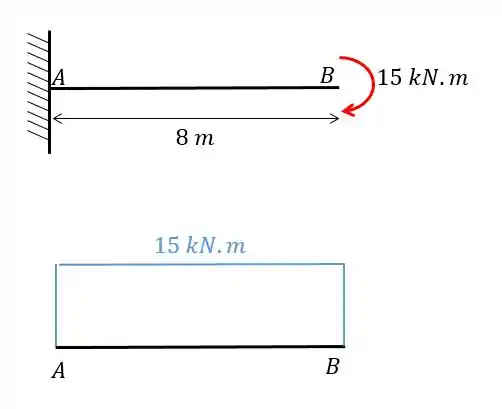
Calcule o deslocamento vertical do ponto B da viga dada abaixo usando o método das tabelas.
Use para todos os trechos da viga.
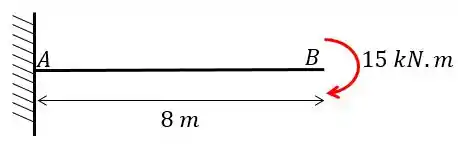
Passo 1
Neste exercício vamos calcular o deslocamento vertical do ponto devido ao momento e para isso vamos utilizar nossa equação de deslocamento. Mas é importante notar que existe apenas uma barra então vamos poder simplificar nossa equação de
Para
Passo 2
A segunda coisa que precisamos fazer é determinar o diagrama de momentos devido a carga que age na nossa estrutura, e o diagrama fica sendo:
Passo 3
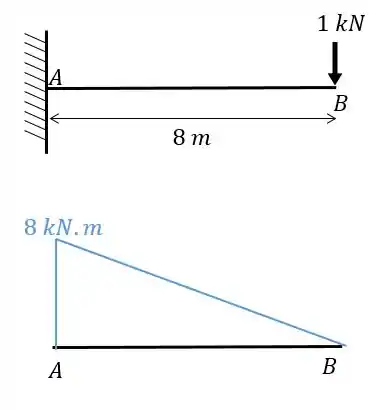
Aplicamos a carga unitária no ponto em que queremos saber o deslocamento, na direção que queremos saber o deslocamento, e determinamos o diagrama de momentos fletores causados por essa carga unitária.
Passo 4
Agora precisamos combinar os dois diagramas de momento fletor.
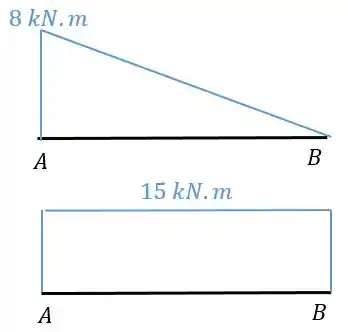
Como estão na mesma direção sabemos que é positivo.
Usando a tabela temos que:
E a fórmula será a combinação desses dois gráficos.
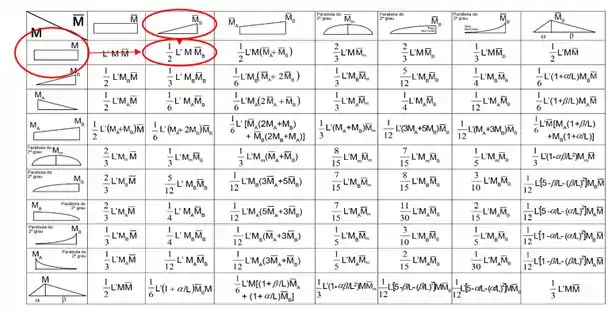
E por fim verificamos se o comprimento da barra se manterá igual
Que para a barra será igual a .
Substituindo na fórmula teremos que
Passo 5
Cálculo da deformação total
Como sabemos que:
Substituindo teremos que
Resposta
Exercício Resolvido #6
José Carlos Süssekind, Curso de análise estrutural, Deformação em estruturas método das forças, 4ºed.RJ:LTC,1980,(pagina),(número do exercício)
Calcule o deslocamento Vertical do ponto C da viga dada abaixo usando o método das tabelas.
Use para todos os trechos da viga.
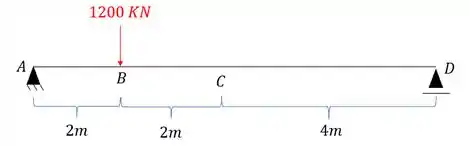
Passo 1
Como vimos na teoria temos um passo a passos bem legal que podemos ir seguindo para determinarmos o deslocamento do nosso ponto.
A primeira coisa que devemos fazer é verificar a inércia. Como foi dito que todas as inercias são iguais, então podemos dizer que:
Se é tudo igual, isso implica que:
Que simplifica a nossa fórmula para
Passo 2
A segunda coisa que precisamos fazer é determinar o diagrama de momentos devido a carga que age na nossa estrutura, e o diagrama fica sendo:
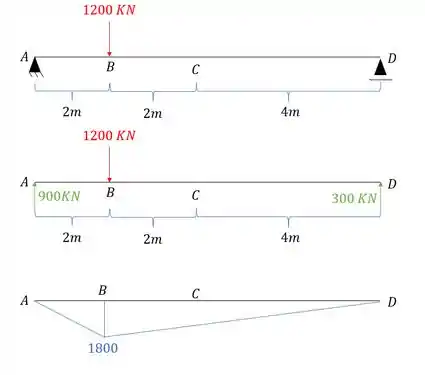
E perceba que fizemos bem separadinho pra ficar fácil de entender.
Passo 3
Aplicamos a carga unitária no ponto em que queremos saber o deslocamento, na direção que queremos saber o deslocamento, e determinamos o diagrama de momentos fletores causados por essa carga unitária.
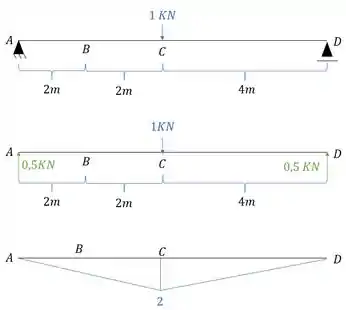
Passo 4
Agora precisamos combinar os dois diagramas de momento fletor.
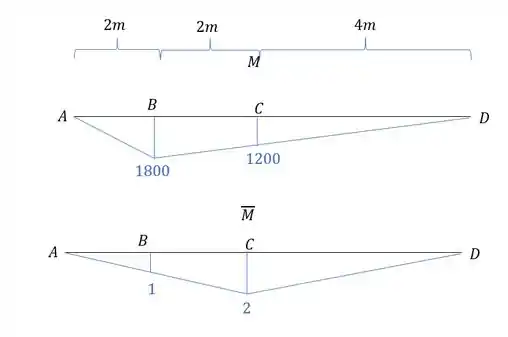
Perceba que temos 3 regiões diferentes, e por isso precisamos combinar cada uma das 3.
- Região AB
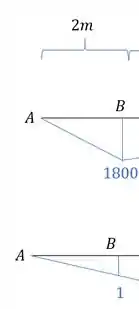
Como estão na mesma direção sabemos que é positivo.
Usando a tabela temos que:

E a fórmula será a combinação desses dois gráficos.
E por fim verificamos se o comprimento da barra se manterá igual
Que para a barra 1 será igual a 2m.
Substituindo na fórmula teremos que
- Trecho BC
- Região CD
Primeiro temos as barras com os seus momentos.
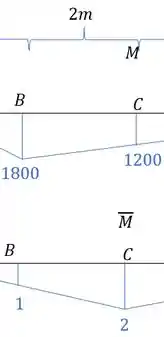
Perceba que a primeira barra, do caso real, para o trecho BC, possui duas regiões diferentes. Uma triangular e uma zero. Enquanto a barra com carregamento virtual é triangular, com isso basta combinas a região certa.
Usando a tabela temos que:

E por fim verificamos se o comprimento da barra se manterá igual
Que para a barra 2 será igual a 2,5m por estarmos combinando diagramas na metade da barra.
Substituindo na fórmula teremos que
Perceba que como os trapézios do problema são invertidos, também invertemos os momentos de dentro dos parênteses.
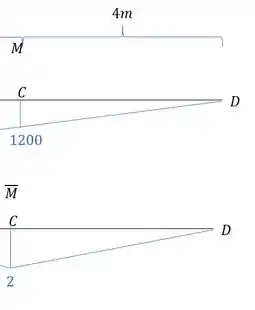
Como estão na mesma direção sabemos que é positivo.
Usando a tabela temos que:
E a fórmula será a combinação desses dois gráficos.
E por fim verificamos se o comprimento da barra se manterá igual
Que para a barra 1 será igual a 4m.
Substituindo na fórmula teremos que
Passo 5
Cálculo da deformação total
Como sabemos que:
Substituindo teremos que
Resposta
Exercício Resolvido #7
José Carlos Süssekind, Curso de análise estrutural, Deformação em estruturas método das forças, 4ºed.RJ:LTC,1980,(pagina),(número do exercício)
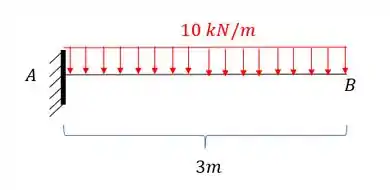
Calcule o deslocamento Vertical do ponto B da viga dada abaixo usando o método das tabelas.
Use para todos os trechos da viga.
Passo 1
Como vimos na teoria temos um passo a passos bem legal que podemos ir seguindo para determinarmos o deslocamento do nosso ponto.
A primeira coisa que devemos fazer é verificar a inércia. Como foi dito que todas as inercias são iguais, então podemos dizer que:
Se é tudo igual, isso implica que:
Que simplifica a nossa fórmula para
Passo 2
A segunda coisa que precisamos fazer é determinar o diagrama de momentos devido a carga que age na nossa estrutura, e o diagrama fica sendo:
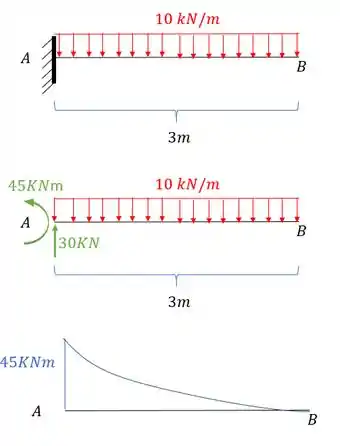
E perceba que fizemos bem separadinho pra ficar fácil de entender.
Passo 3
Aplicamos a carga unitária no ponto em que queremos saber o deslocamento, na direção que queremos saber o deslocamento, e determinamos o diagrama de momentos fletores causados por essa carga unitária.
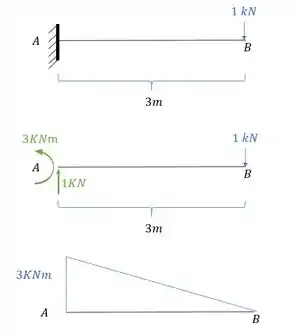
Passo 4
Agora precisamos combinar os dois diagramas de momento fletor.
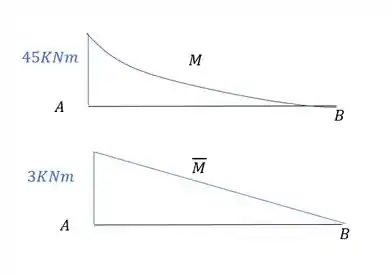
Como estão na mesma direção sabemos que é positivo.
Usando a tabela temos que:
E a fórmula será a combinação desses dois gráficos.
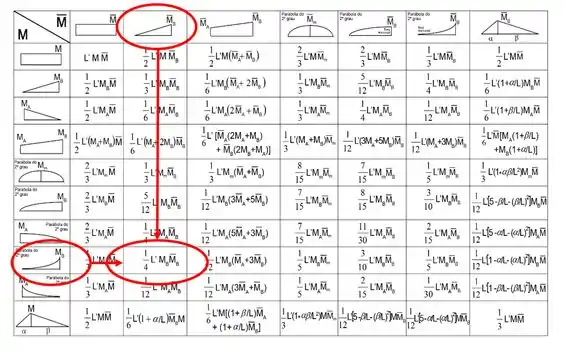
E por fim verificamos se o comprimento da barra se manterá igual
Que para a barra 1 será igual a 3m.
Substituindo na fórmula teremos que
Passo 5
Cálculo da deformação total
Como sabemos que:
Substituindo teremos que
Resposta
Exercício Resolvido #8
José Carlos Süssekind, Curso de análise estrutural, Deformação em estruturas método das forças, 4ºed.RJ:LTC,1980,(pagina),(número do exercício)
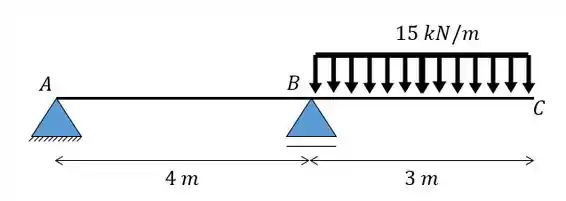
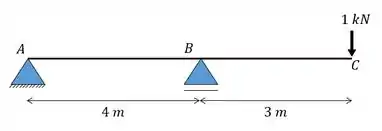
Calcule o deslocamento vertical do ponto C da viga dada abaixo usando o método das tabelas.
Use para todos os trechos da viga.
Passo 1
Como vimos na teoria temos um passo a passos bem legal que podemos ir seguindo para determinarmos o deslocamento do nosso ponto.
A primeira coisa que devemos fazer é verificar a inércia. Como foi dito que todas as inercias são iguais, então podemos dizer que:
Se é tudo igual, isso implica que:
Como a nossa equação é dada por:
Então podemos simplificar a nossa fórmula para
Passo 2
A segunda coisa que precisamos fazer é determinar o diagrama de momentos devido a carga que age na nossa estrutura, e o diagrama fica sendo:
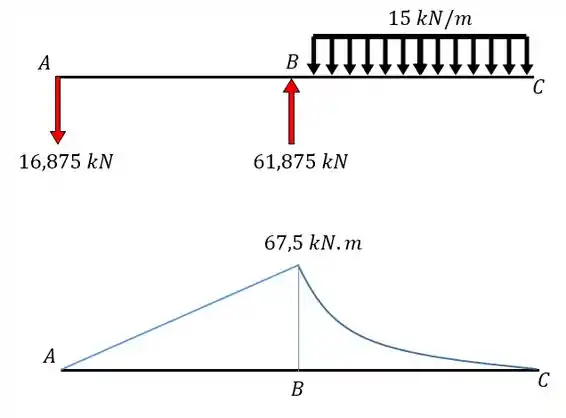
E perceba que existem duas funções distintas, uma para cada barra.
Passo 3
Aplicamos a carga unitária no ponto em que queremos saber o deslocamento, na direção que queremos saber o deslocamento, e determinamos o diagrama de momentos fletores causados por essa carga unitária.
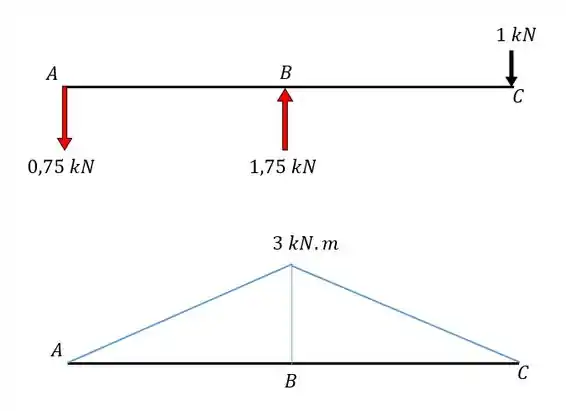
Passo 4
Determinação das combinações para cada uma das barras.
- Trecho AB
- Trecho BC
Primeiro temos as barras com os seus momentos.
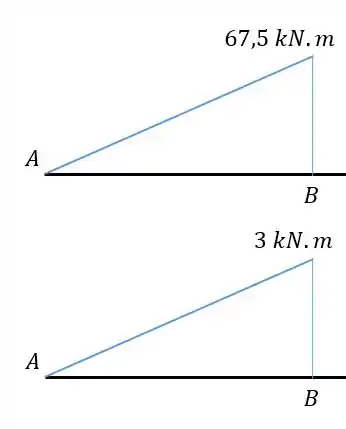
Como estão na mesma direção sabemos que é positivo.
Usando a tabela temos que:

E a fórmula será a combinação desses dois gráficos.
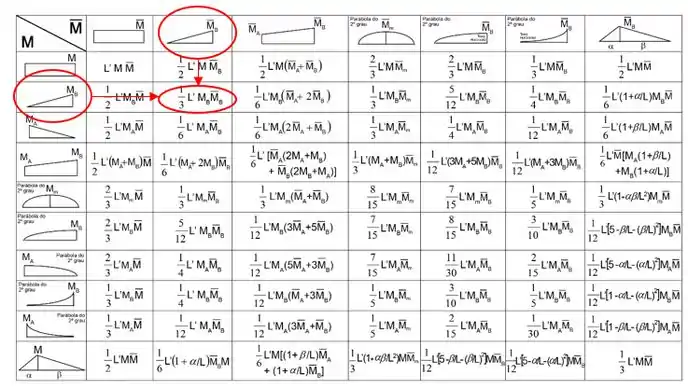
E por fim verificamos se o comprimento da barra se manterá igual
Que para a barra será igual a .
Substituindo na fórmula teremos que
Primeiro temos as barras com os seus momentos.
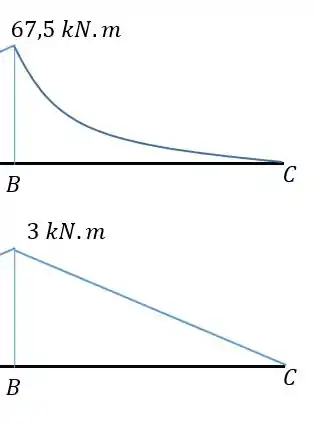
Usando a tabela temos: 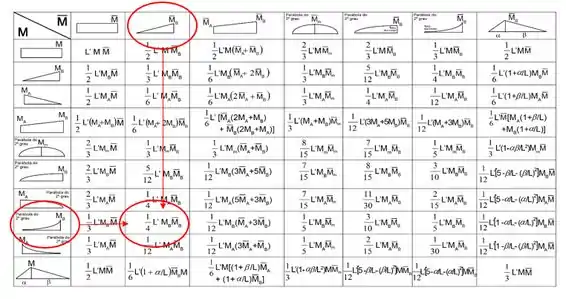
E por fim verificamos se o comprimento da barra se manterá igual
Que para a barra será igual a .
Substituindo na fórmula teremos que
Passo 5
Cálculo da deformação total
Como sabemos que:
Substituindo teremos que