Passo a Passo método dos deslocamentos
Produzido por Pablo RicardoTeoria
Introdução
Até aqui aprendemos a solucionar problemas usando o método das forças, mas agora iremos aprender a solucionar os nossos problemas hiperestáticos através do método dos deslocamentos, e vamos ver que a ideia continua a mesma, mas alguns princípios mudam. Vamos entender isso por partes:
O método das forças
No método das forças aprendemos a soltar vínculos, e com esses vínculos soltos definíamos deformações que definíamos por exemplo como:
Em que sabíamos que significava que era um deslocamento no ponto 1 (primeiro índice 1) e que ocorria nos sistema 2 (segundo índice 2) ou seja, os índices marcavam primeiro o ponto em que ocorria, e depois o local em que ocorria, certo?
Mas como definíamos o ponto que seria chamado de 1? Era exatamente o ponto em que estava o nosso hiperestático, ou seja, quando olhávamos a deformação:
Sabíamos que ela significava: olha temos uma deformação no ponto 1 devido a um hiperestático no ponto 2. Certo? E o que a gente fazia depois? Somávamos todas as deformações que ocorriam naquele ponto e igualávamos a zero porque sabíamos que o hiperestático liberava um movimento que não deveria existir, logo a soma de todos os casos deveria dar zero, e com isso surgia o nosso sisteminha:
E fazíamos a mesma coisa para o ponto 2 em que resolvíamos um sistema de equações para achar as forças e que faziam o nosso sistema zerar os deslocamentos liberados, certo?
Isso é um resumão bem rápido pra gente entender como vai funcionar no método dos deslocamentos.
O método dos deslocamentos
De maneira análoga vamos seguir o mesmo padrão, imagine o seguinte pórtico aqui em baixo:
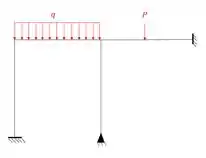
No método das forças nos contávamos o número de incógnitas e de equações, e assim descobríamos o número de hiperestáticos, certo? Aqui iremos fazer algo diferente. Lembra que aprendemos a contar deslocabilidades externas e internas? Então vamos fazer isso aqui, e esse vai ser o nosso primeiro passo:
Passo 1: determinação das deslocabilidades externas e internas
Sabemos que para determinar o número de deslocabilidades internas, precisamos contar os nós que seguem a seguinte regra:
- Não são nós de apoio
- Não são nós rotulados
Sendo assim as nossas deslocabilidades internas serão
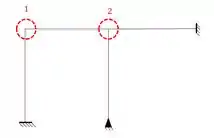
Então já sabemos que temos duas deslocabilidades internas.
As externas a gente nomeia os nós:
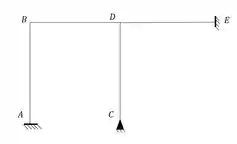
E após nomear vemos as possíveis deslocabilidades:
- Os nós A, C e E são indeslocaveis, logo, não terão deslocabilidades externas
- O nó D está ligado aos nós C e E que também são indeslocaveis, logo o nó D também será
- O nó B está ligado aos nós A e D que são indeslocaveis, logo o nó B também é, e com isso descobrimos que não temos deslocabilidades externas.
- Passo 2: travamos essas deslocabilidades e numeramos elas
- Passo 3: o que eu faço com e
- Passo 4: determinação do sistema 0
Agora que a magica acontece, lembra que no método das forças a gente soltava os nós e substituíamos por hiperestáticos? E assim tínhamos uma estrutura isostática para resolver? Aqui iremos pelo caminho contrário, iremos travar os nós, e nesse caso como eles só podem rodar (pois só temos deslocabilidades internas) iremos pôr uma chapa para representar o travamento a rotação.
Mas e se tivesse deslocabilidades externas? Ai colocaríamos o nosso amigo apoio do primeiro gênero para travar o movimento, mas no nosso exemplo não temos esse nosso amigo. Então botando a chapa e numerando ela, teremos que:

E olha só, essas nossas chapinhas estão travando a rotação certo? Ou seja, a minha estrutura deveria rotacionar, mas eu impedi isso, então não irão aparecer deformações que deveriam acontecer, então eu vou ter que forçar essas deformações a aparecerem, essas deformações eu vou chamar de e que são análogos aos meus e do método das forças, além do mais, se você lembrar bem, assim como eu forço a aparição de e por colocar as chapas , eu também forçava a aparição de e por quebrar os vínculos, ou seja, os nosso métodos estão se comportando de maneira análoga.
Quando eu não sabia o valor de e o que eu fazia? Supunha um sistema em que e fossem unitários, e um sistema 0 com a carga externa , calculava as deformações ,, e e a deformação devido a carga externa ( ia para o meu sistema certo?
Aqui o princípio é o mesmo, só que ao invés de serem forças unitárias, serão rotações unitárias. Mas como vamos fazer isso?
A primeira coisa que devemos saber é que iremos usar o nosso conceito de momentos fletores devido a rotação unitária, ou seja, iremos usar a rigidez de cada nó separadamente, para isso temos que entender que essa rigidez aqui vai ser chamada da seguinte maneira:

Ou seja, se tivermos a seguinte rigidez:
Significará, a rigidez no ponto 1 (ou no nosso exemplo, na chapa 1) quando rotacionamos a chapa 2 (que rotacionamos a chapa 2 no sistema 2).
Então agora só precisamos determinar os nossos sistemas e entender como determinar a rigidez:
- Primeiro determinamos os sistemas
- Sistema 0
- Passo 5: determinação do sistema 1
- Sistema 1
- Passo 6: determinação do sistema 2
- Sistema 2
É o sistema em que a carga externa vai agir, e no sistema zero iremos determinar e usando o conceito de momentos de engastamento perfeito, que nada mais é que usar a tabela abaixo para detemirnar os momentos que agem em cada uma das chapas.
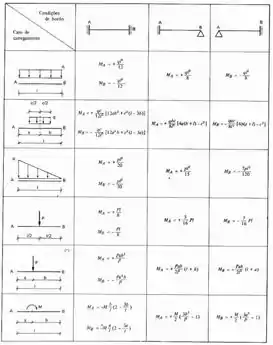
Perceba que as nossas chapas impedem o único movimento que o nó poderia fazer, ou seja, é como se o nosso pórtico tivesse nós que são engastados, dessa maneira, se separássemos o nosso pórtico, teríamos os seguintes trechos de vigas:
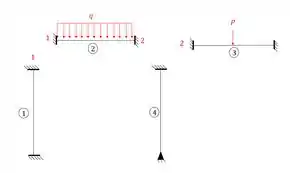
Perceba que o nó 1 poderia receber contribuições tanto da barra 1 quanto da barra 2. Mas nesse caso como só tem carga na barra 2, só essa vai contribuir com ele. Já o nó 2 vai receber contribuição tanto da barra 2 quanto da barra 3, sendo assim, se usarmos a nossa tabela de engastamentos perfeitos teremos que:
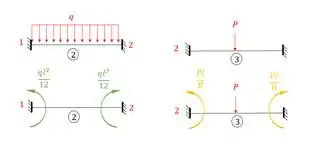
Agora pensa comigo, qual o momento que age na chapa 1? Esse vai ser o nosso , que vamos escrever como:
E o que age na chapa 2? Veja que temos duas contribuições, ambas devem ser contabilizadas, lembrando que sentido horário é negativo, sendo assim teremos que:
E assim determinamos as rigidezes referentes ao sistema zero.
O sistema 1 nada mais é que analisarmos o que acontece com as chapas do pórtico se rotacionarmos apenas a chapa 1. No sistema 1 determinamos todas as rigidezes que o segundo índice é 1, ou seja, ,..... e assim por diante. Lembre-se que não conhecemos , por isso iremos supor ele unitário, e sempre que temos uma rotação unitária, que tabela devemos usar? Essa aqui de baixo:
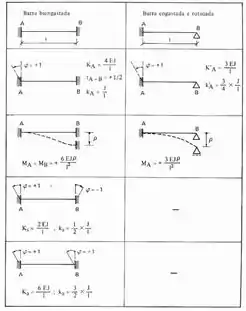
Como no exemplo anterior já mostramos o pórtico separado, agora já podemos ir direto pois fica mais fácil de visualizar o conceito, então imagine a nossa chapa rotacionada de 1°, teríamos isso aqui:
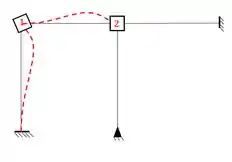
Um macete legal de se perceber é que eu sempre giro a chapa no sentido anti-horário, porque assim eu sei que os momentos que irão aparecer serão positivos, pois sempre se lembre que o sentido anti-horário é o nosso positivo.
Perceba que como a chapa 1 representa um engaste, usaremos da nossa tabela o seguinte conceito:
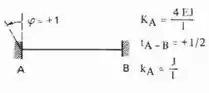
Sendo assim teremos que os momentos que aparecem são:
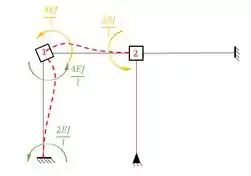
Agora só lembrar o momento que aparece no ponto 1 devido a rotação da chapa 1 no sistema 1 será:
Como são os dois no sentido anti-horário, ambos são positivo.
Lembra que no sistema 1 sempre determinamos as rigidezes que terminam em 1, ou eu posso pensar pela regrinha.
Qual o momento que age no ponto 2 devido a uma rotação da chapa 1 no sistema 1:
Como o primeiro índice sempre é o ponto em que ocorre, teremos que:
O sistema 2 nada mais é que analisarmos o que acontece com as chapas do pórtico se rotacionarmos apenas a chapa 2. No sistema 2 determinamos todas as rigidezes que o segundo índice é 2, ou seja, ,..... e assim por diante. Lembre-se que não conhecemos , por isso iremos supor ele unitário, e sempre que temos uma rotação unitária, que tabela devemos usar? Essa aqui de baixo:
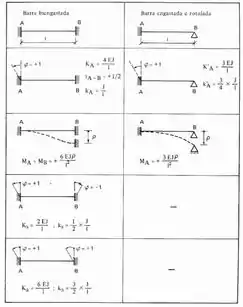
Como no exemplo anterior já mostramos o pórtico separado, agora já podemos ir direto pois fica mais fácil de visualizar o conceito, então imagine a nossa chapa rotacionada de 1°, teríamos isso aqui:
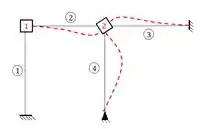
Perceba que novamente girei a chapa no sentido anti-horário, porque assim eu sei que os momentos que irão aparecer serão positivos, pois sempre se lembre que o sentido anti-horário é o nosso positivo.
Perceba que a chapa 2 irá representar um Bi-engastamento para as barras 2 e 3, e assim usaremos a seguinte parte da tabela:
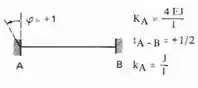
mas para barra 4 ela irá representar um engaste e um apoio, sendo assim usaremos esse trecho da tabela aqui:
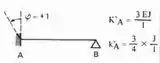
Sendo assim teremos que os momentos que aparecem são:
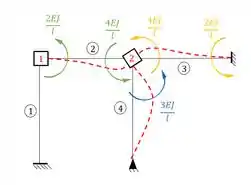
Agora só lembrar o momento que aparece no ponto 2 devido a rotação da chapa 2 no sistema 2 será:
Como são os três no sentido anti-horário, todos são positivos.
Lembra que no sistema 2 sempre determinamos as rigidezes que terminam em 2, ou eu posso pensar pela regrinha.
Qual o momento que age no ponto 1 devido a uma rotação da chapa 2 no sistema 2:
Como o primeiro índice sempre é o ponto em que ocorre, teremos que:
Agora basta lembrar do que fazíamos no método das forças, tudo referente ao ponto 1 somado tem que zerar, porém lembre-se que os ’s definidos nos sistemas 1 e 2 eram unitários, e nosso objetivo é determinar os verdadeiros, ou seja, basta multiplicar, sendo assim teremos que o nosso sistema para o ponto 1 será:
E para o ponto 2 será:
E o nosso sistema de equações a ser resolvido será:
Se substituirmos tudo que encontramos ao longo do nosso problema teremos que:
Perceba que se multiplicarmos ambos os sistemas por , e isolarmos os termos sem e , teremos que:
Ou seja, a solução do sistema fica mais simples, e essa é uma estratégia que eu costumo usar para resolver esse tipo de problema, eu sempre monto o sistema inteiro e no final multiplico tudo por (lembrando que usamos isso apenas se todos os comprimentos das barras forem iguais, se não forem, basta trocar o termo pelo termo 1 e usar a seguinte simplificação ) , para poder simplificar. Mas perceba que você pode usar qualquer multiplicação que simplifique, a ideia é conseguir tirar tanto de quanto de o termo EJ, se conseguirmos tirar desses caras os termos EJ, o sistema fica mais simples. Isso é o que chamamos de rigidez relativa e podemos usar sempre qualquer valor, mas a ideia é facilitar a nossa vida. Vale lembrar que não somos obrigados a rotacionar as nossas chapas de um valor unitário, eu só fiz isso pra facilitar a nossa vida, mas por exemplo, se rotacionarmos a chapa de , basta pegarmos as nossas rigidezes e multiplicarmos pelo valor de se isso for facilitar a nossa vida, mas se lembre que se rotacionamos de 1 unidade, sempre vamos ter o valor da nossa rigidez verdadeira, então sempre vai depender do que estamos querendo facilitar.
E perceba que, enquanto o método das forças nós dava como respostas forças, o método dos deslocamentos nós dá como respostas deslocamentos, mas e se eu quiser os diagramas? Ai basta olhar aqui embaixo:
Para isso basta nomearmos os nós do nosso pórtico como vemos aqui em baixo:
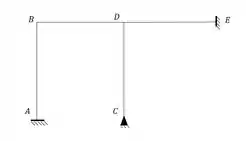
E para determinação dos esforços basta fazermos:
Em que i é o ponto em que queremos saber o esforço.
Ou seja, se quisermos saber, por exemplo, o momento no ponto A deveremos fazer:
O cortante? Usamos a mesma fórmula:
Para as reações de apoio, como temos os momentos de todos os nós, basta fazermos um equilíbrio de forças e momentos para cada umas das barras do pórtico para podermos determinar as reações de apoio pela equação acima, e ai faríamos:
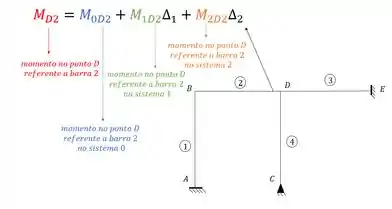
Obs: perceba que por exemplo, o ponto D possui 3 barras chegando nele, então como determinamos o momento nele? É so fazer o momento atuando no ponto D para cada uma das barras, ou seja, se colocarmos no nosso índice um numero que represente a barra, podemos esquecer:
O método dos deslocamentos
Passo 1: determinação das deslocabilidades externas e internas
Exercícios Resolvidos
Exercício Resolvido #1
Origem do Exercício
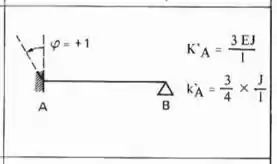
Determine o valor de no pórtico dado abaixo:
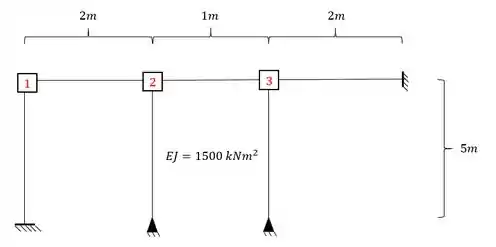
Passo 1
Perceba que temos que determinar o valor de , certo? Para isso temos que entender o que isso significa, para isso precisamos entender o que cada termo da nossa deformação significa.

Ou seja, podemos dizer que queremos saber qual a rigidez no ponto 3 quando deformamos a chapa 2, ou seja, o primeiro termo diz o local que queremos saber (3) e o segundo termo diz o nó que temos que deformar (2).
Sendo assim teremos que:
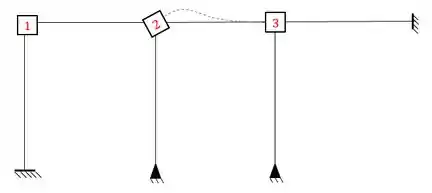
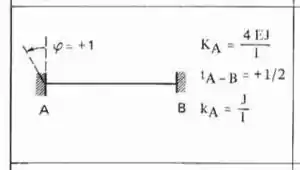
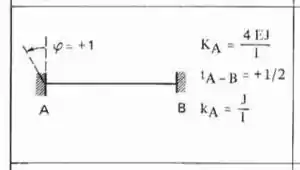
Perceba que temos a chapa em 2 e em 3, ou seja, uma viga Bi-engastada. Ou seja, a fórmula que temos que usar é:
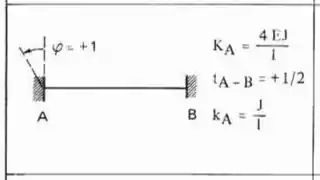
Sendo assim teremos que:
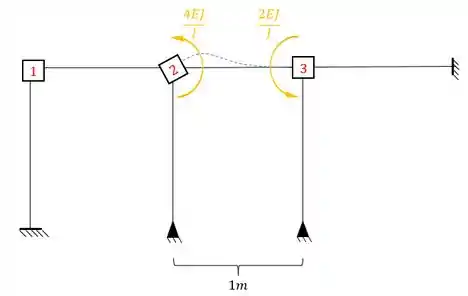
Ou seja, a rigidez que acontece no ponto 3 devido a rotação em 2 é dado por:
Resposta
Exercício Resolvido #2
Origem do Exercício
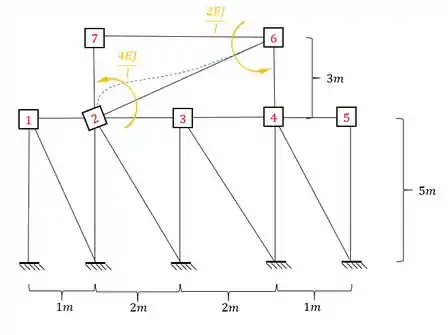
Determine o valor de no pórtico dado abaixo:
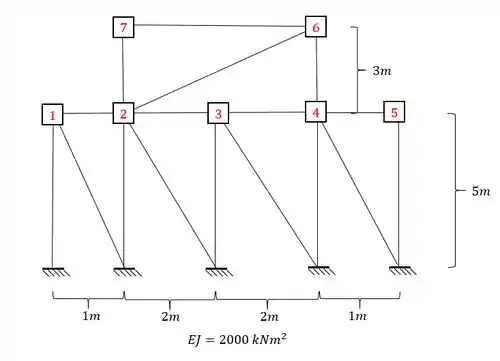
Passo 1
Perceba que temos que determinar o valor de , certo? Para isso temos que entender o que isso significa, para isso precisamos entender o que cada termo da nossa deformação significa.

Ou seja, podemos dizer que queremos saber qual a rigidez no ponto 6 quando deformamos a chapa 2, ou seja, o primeiro termo diz o local que queremos saber (6) e o segundo termo diz o nó que temos que deformar (2).
Sendo assim teremos que:
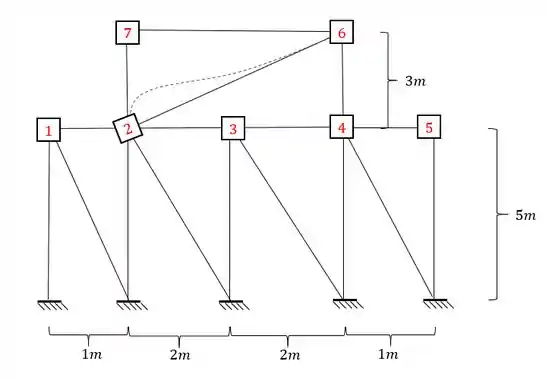
Perceba que temos a chapa em 2 e em 6, ou seja, uma viga Bi-engastada. Ou seja, a fórmula que temos que usar é:
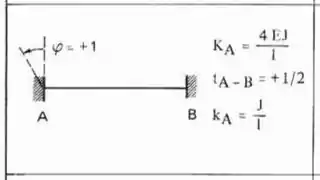
Sendo assim teremos que:
Ou seja, a rigidez que acontece no ponto 6 devido a rotação em 2 é dado por:
Porém perceba que não temos o comprimento da barra, para isso só precisamos fazer Pitágoras, sendo assim teremos que:
Substituindo teremos que:
Resposta
Exercício Resolvido #3
José Carlos Sussekind, Curso de análise estrutural 3, 7ª ed. Rio de Janeiro: Globo, 1987, pp. 172. ex. 10.2 (Adaptado)
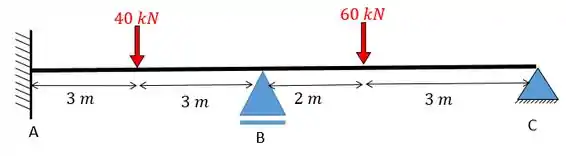
Determine e resolva equação da estrutura dada abaixo. Dado:
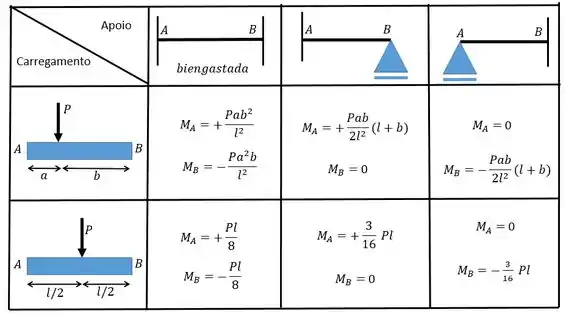
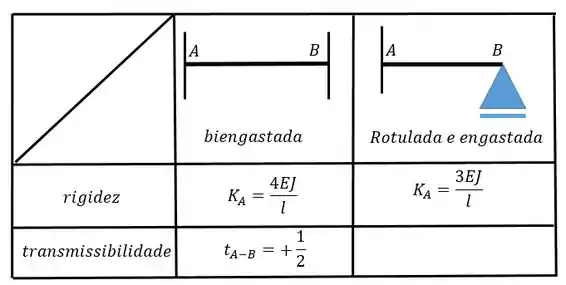
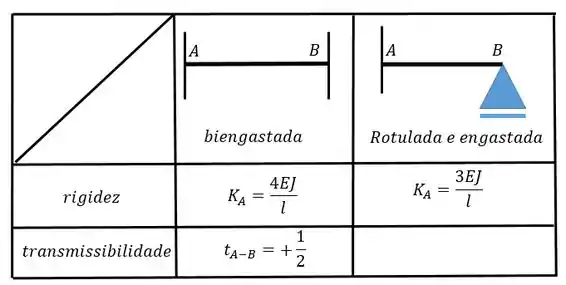
Utilize as seguintes tabelas:
Passo 1
Fala, pessoal!!! A questão pede para determinarmos as equações que regem esse problema e para isso a primeira coisa que devemos fazer é saber trocar corretamente os apoios. Neste caso só vamos precisar impedir a rotação em obtendo:
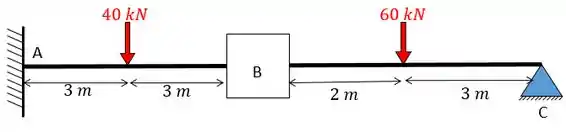
Agora sabemos que temos 1 chapas na nossa estrutura, como podemos ver ali em cima. Como temos apenas uma chapa vamos ter uma equação da forma:
Mas a questão não para aí né, a gente tem que achar os valores de e também! Vamos ver isso com mais detalhes nos próximos passos!
Passo 2
Para determinar os valores desses coeficientes nós precisamos combinar o carregamento com a condição dos apoios através da tabelinha:
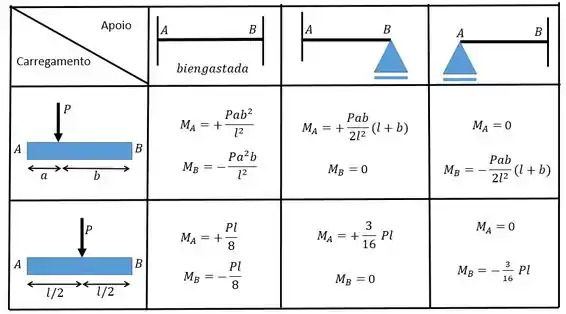
Vamos descobrir primeiro o valor de então!
Olhando a conta para cara barra teremos que:
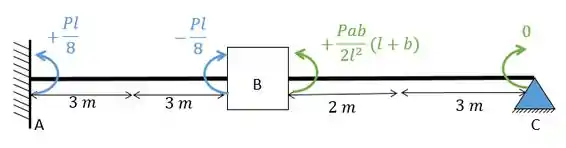
Substituindo os valores vamos ter:
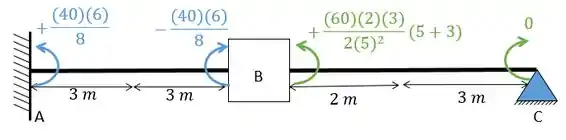
Ou seja, o valor de é:
Passo 3
Agora vamos calcular . Para isso vamos precisar da outra tabelinha:
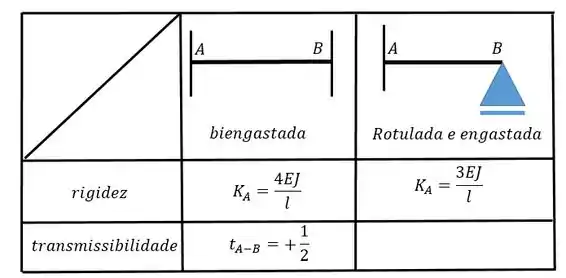
Vamos rotacionar a chapa e obtemos:
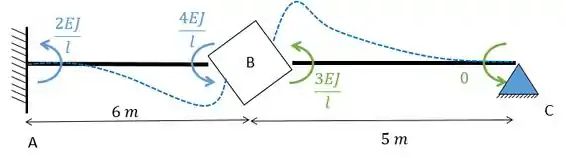
Dessa forma vamos ter:
Passo 4
Organizando o sistema temos que:
Substituindo:
E podemos calcular a deformação:
Resposta
Exercício Resolvido #4
José Carlos Sussekind, Curso de análise estrutural 3, 7ª ed. Rio de Janeiro: Globo, 1987, pp. 37. (Adaptado)
Determine e resolva equação da estrutura dada abaixo. Dado:
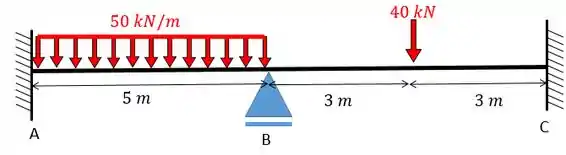
Utilize as seguintes tabelas:
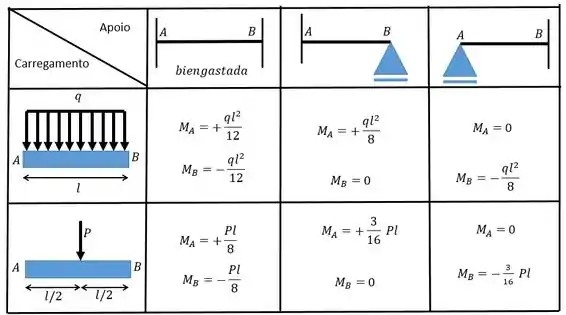
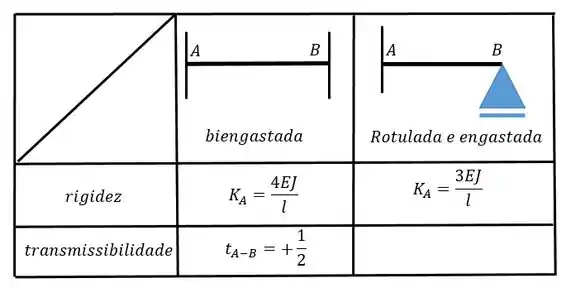
Passo 1
Fala, pessoal!!! A questão pede para determinarmos as equações que regem esse problema e para isso a primeira coisa que devemos fazer é saber trocar corretamente os apoios. Neste caso só vamos precisar impedir a rotação em obtendo:
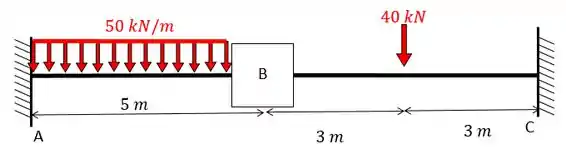
Agora sabemos que temos 1 chapas na nossa estrutura, como podemos ver ali em cima. Como temos apenas uma chapa vamos ter uma equação da forma:
Mas a questão não para aí né, a gente tem que achar os valores de e também! Vamos ver isso com mais detalhes nos próximos passos!
Passo 2
Para determinar os valores desses coeficientes nós precisamos combinar o carregamento com a condição dos apoios através da tabelinha:
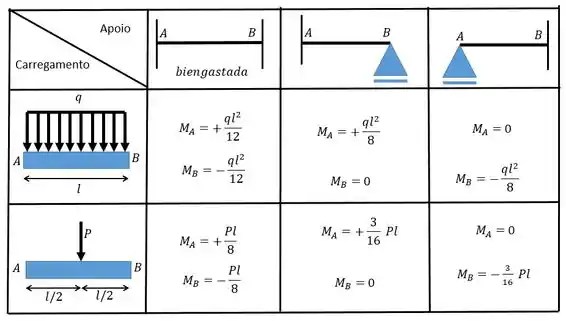
Vamos descobrir primeiro o valor de então!
Olhando a conta para cara barra teremos que:
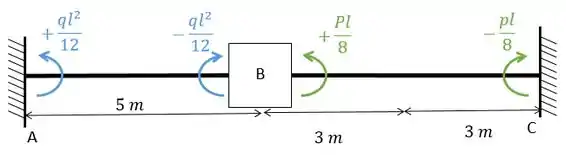
Substituindo os valores vamos ter:
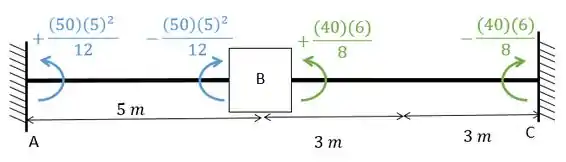
Ou seja, o valor de é:
Passo 3
Agora vamos calcular . Para isso vamos precisar da outra tabelinha:
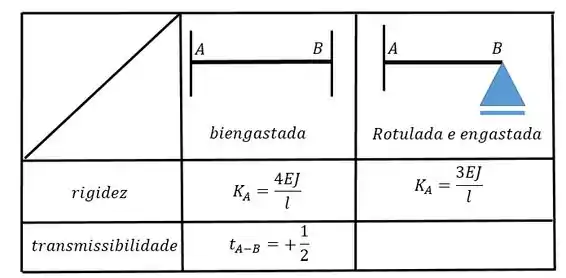
Vamos rotacionar a chapa e obtemos:
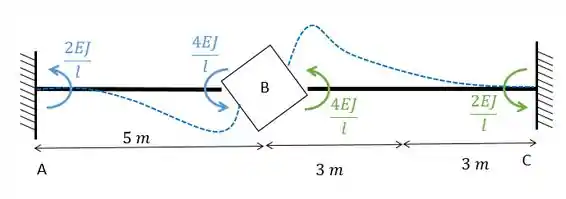
Dessa forma vamos ter:
Passo 4
Organizando o sistema temos que:
Substituindo:
E podemos calcular a deformação:
Resposta
Exercício Resolvido #5
Origem do Exercício
Determine o valor de no pórtico dado abaixo:
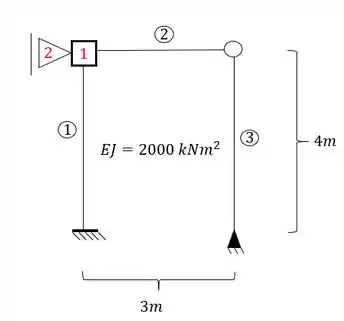
Passo 1
Perceba que temos que determinar o valor de , certo? Para isso temos que entender o que isso significa, para isso precisamos entender o que cada termo da nossa deformação significa.

Ou seja, podemos dizer que queremos saber qual a rigidez no ponto 2 quando deformamos a chapa 1, ou seja, o primeiro termo diz o local que queremos saber (2) e o segundo termo diz o nó que temos que deformar (1).
Sendo assim teremos que:
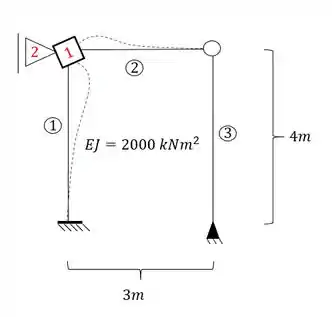
Perceba que na barra 1 temos um engaste e uma chapa, que representam um estrutura Bi-engastada. Já na barra 2 temos uma chapa de um lado e um rotula do outro, que representa um apoio, logo, uma estrutura engastada e apoiada, sendo assim as fórmulas a serem usadas são:
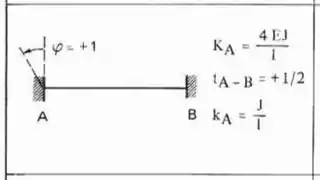
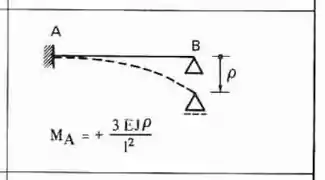
Sendo assim teremos que:
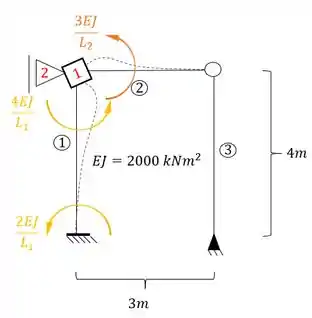
Como desejamos saber o que acontece no ponto 2 (que é um apoio) devido a rotação da chapa 1, precisamos definir o valor das rigidezes, e determinar a reação no apoio 2, e assim determinaremos exatamente o nosso valor de , sendo assim teremos que:
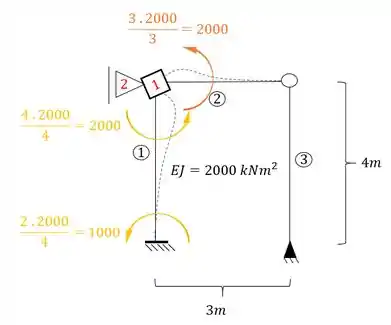
O único que produz reação horizontal é a barra 1, sendo assim teremos que:
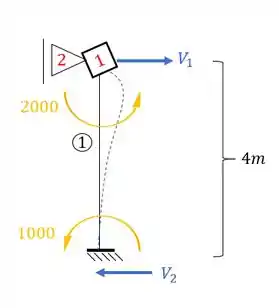
Como mantemos a direção e sinal calculados para V1, e V2 tem o mesmo valor e o sentido, temos que a reação de apoio, e consequentemente o valor de , será:
Resposta
Exercício Resolvido #6
Origem do Exercício
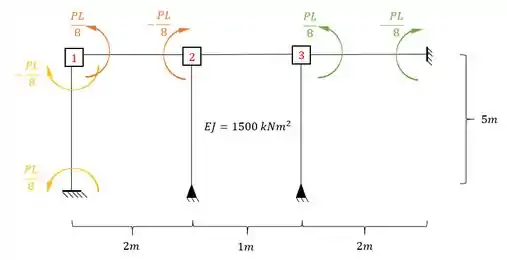
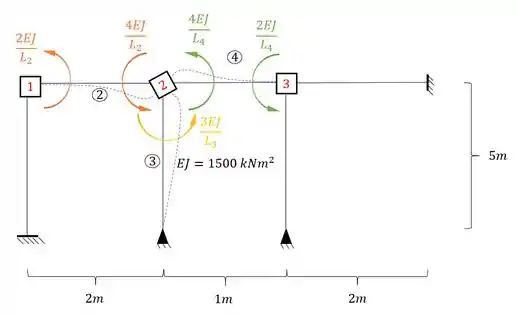
Determine o sistema de equações da estrutura dada abaixo:
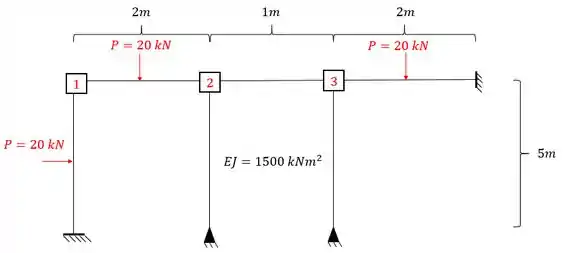
Passo 1
Sabemos que temos 3 chapas na nossa estrutura, como podemos ver ali em cima. Uma parada legal a ser feita é contabilizar tudo que devemos determinar em cada chapa, se fizermos isso obtemos o seguinte:

Sabendo já o que tem que determinar, vamos fazer um de cada vez.
Passo 2
Vamos determinar primeiro os valores de , e . Para determinar isso precisamos da seguinte tabela:
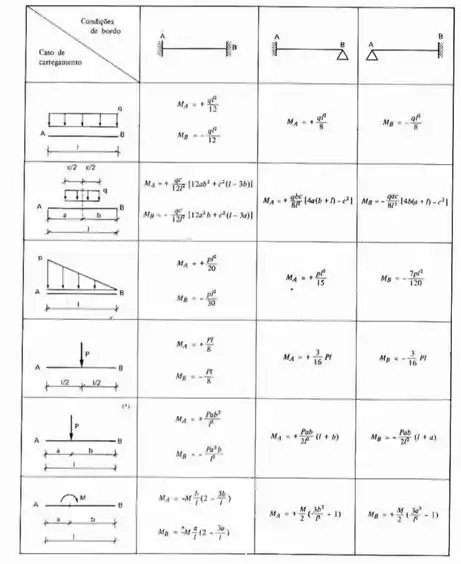
Olhando a conta para cara barra teremos que:
Trocando os valores teremos que:
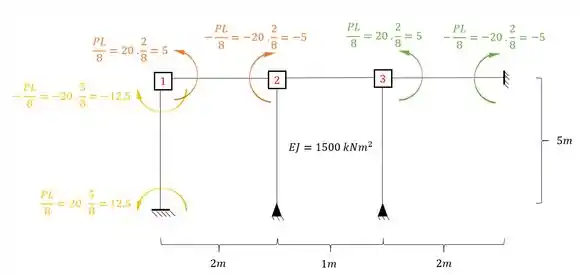
Assim teremos que:
Passo 3
Agora vamos rotacionar a chapa 1, para podermos determinar os valores de , e .
Perceba que as duas barras que chegam na chapa 1 são Bi-engastadas, logo a fórmula a ser usada é:
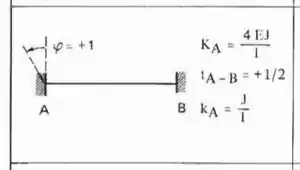
Substituindo certinho temos que:
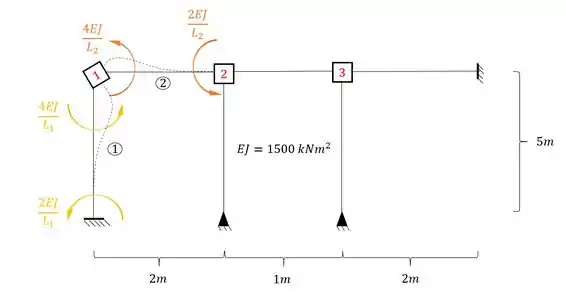
Juntando o que têm-se em cada nó, teremos que:
Passo 4
Agora vamos rotacionar a chapa 2, para podermos determinar os valores de , e .
Perceba que as duas barras horizontais que chegam na chapa 2 são Bi-engastadas, e a barra vertical que chega na chapa 2 é engastada e apoiada, logo as fórmulas a serem usadas são:
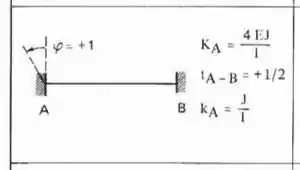
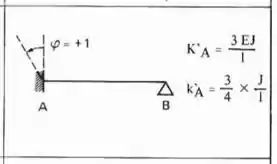
Substituindo certinho temos que:
Juntando o que têm-se em cada nó, teremos que:
Passo 5
Agora vamos rotacionar a chapa 3, para podermos determinar os valores de , e .
Perceba que a barra horizontal que chega na chapa 3 é Bi-engastadas, e a barra vertical que chega na chapa 3 é engastada e apoiada, logo as fórmulas a serem usadas são:
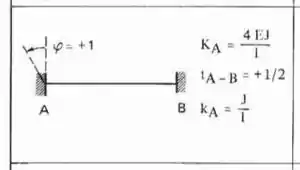
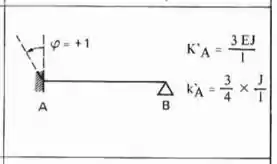
Substituindo certinho temos que:
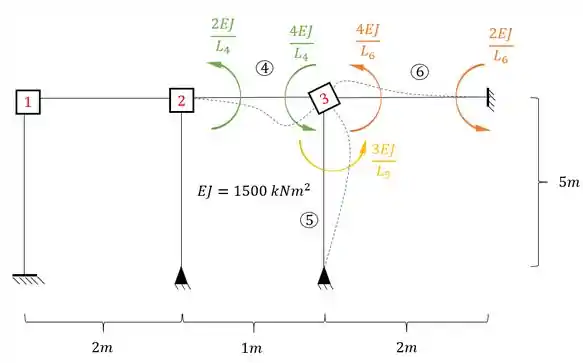
Juntando o que têm-se em cada nó, teremos que:
Passo 6
Organizando o sistema temos que:
Substituindo temos que:
Assim o nosso sistema será:
Resposta
Exercício Resolvido #7
Elaboração própria
Determine e resolva equação da estrutura dada abaixo. Dado:
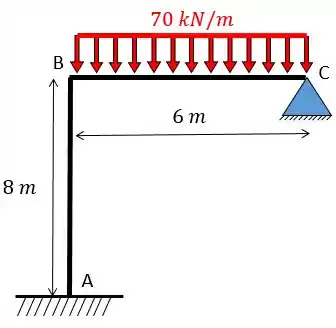
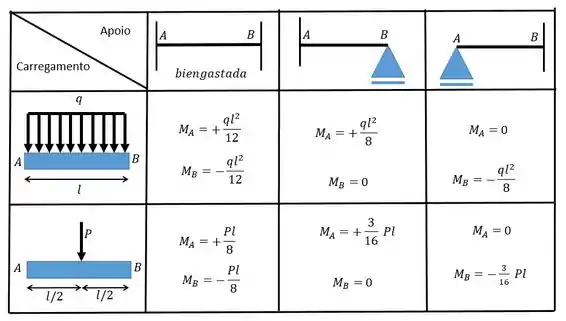
Utilize as seguintes tabelas:
Passo 1
Fala, pessoal!!! A questão pede para determinarmos as equações que regem esse problema e para isso a primeira coisa que devemos fazer é saber trocar corretamente os apoios. Neste caso só vamos precisar impedir a rotação em obtendo:
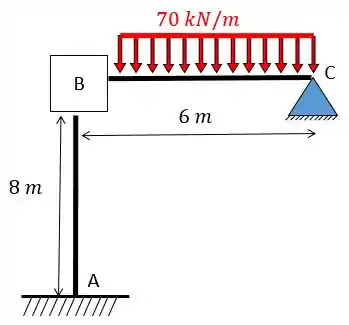
Agora sabemos que temos 1 chapas na nossa estrutura, como podemos ver ali em cima. Como temos apenas uma chapa vamos ter uma equação da forma:
Mas a questão não para aí né, a gente tem que achar os valores de e também! Vamos ver isso com mais detalhes nos próximos passos!
Passo 2
Para determinar os valores desses coeficientes nós precisamos combinar o carregamento com a condição dos apoios através da tabelinha:
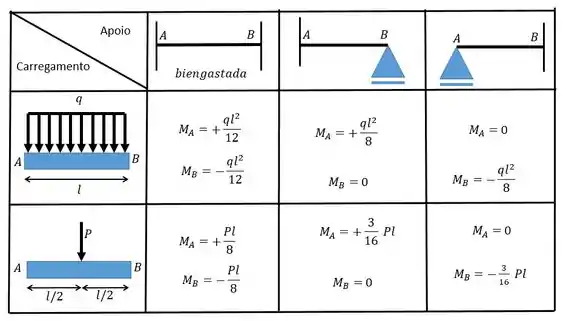
Vamos descobrir primeiro o valor de então!
Olhando a conta para cara barra teremos que:
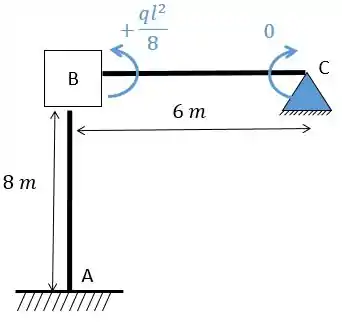
Perceba que não há carga na barra !
Substituindo os valores vamos ter:
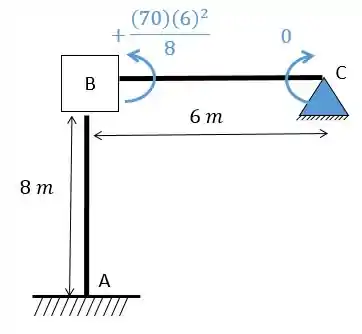
Ou seja, o valor de é:
Passo 3
Agora vamos calcular . Para isso vamos precisar da outra tabelinha:
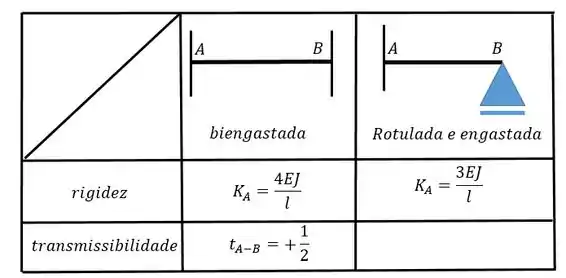
Vamos rotacionar a chapa e obtemos:
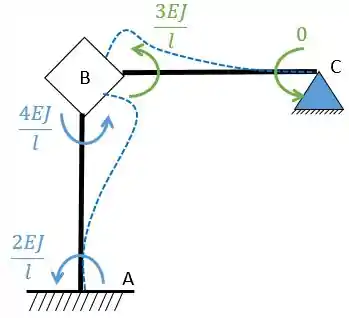
Dessa forma vamos ter:
Passo 4
Organizando o sistema temos que:
Substituindo:
E podemos calcular a deformação:
Resposta
Exercício Resolvido #8
Origem do Exercício
Determine as seguintes rigidezes: (
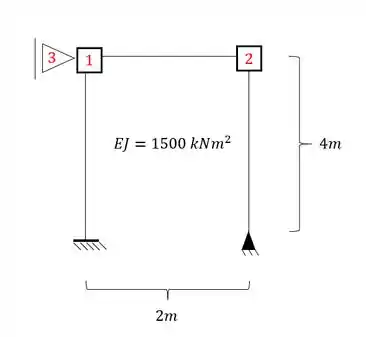
Passo 1
Sabemos que temos 2 chapas na nossa estrutura e um apoio do primeiro gênero, como podemos ver ali em cima. Uma parada legal a ser feita é contabilizar tudo que devemos determinar em cada chapa e apoio , se fizermos isso obtemos o seguinte:

Como não temos carregamento, não precisamos determinar , nem e nem .
Passo 2
Agora vamos rotacionar a chapa 1, para podermos determinar os valores de , e .
Perceba que as duas barras que chegam na chapa 1 são Bi-engastadas, logo a fórmula a ser usada é:
Substituindo certinho temos que:
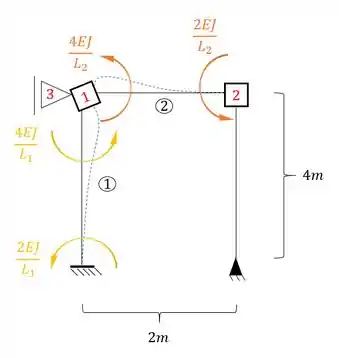
Juntando o que têm-se em cada nó, teremos que:
Para o valor de precisamos fazer a reação de apoio, sendo assim teremos que:
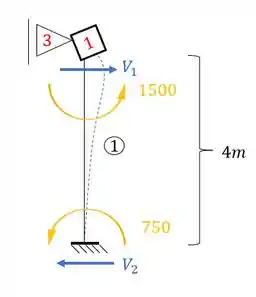
O que podemos admitir para facilitar o cálculo é que o sentido da reação do apoio do primeiro gênero é no mesmo sentido da reação que calculamos na barra, ou seja, se acharmos V1 pra frente, o final é positivo porque a reação no apoio é positiva. Logo:
Obs:. Isso acontece porque a reação que calculamos age na estrutura, ou seja, temos que passar ela com o sinal invertido para saber como ela age no apoio ( ou seja, ela está para frente da maneira que calculamos, mas invertemos o seu sentido para ela agir no apoio, ou seja, para trás. Se ele age para trás no apoio, qual vai ser a reação do apoio? Pra frente, certo? Ou seja, o mesmo sentido do vetor que calculamos ali em cima, que é pra frente, viu como assim é mais complexo? Então só lembrar que a reação de apoio tem o mesmo sentido do vetor calculado, que fica tudo lindo.
Passo 3
Agora vamos rotacionar a chapa 2, para podermos determinar os valores de , e .
Perceba que a barra horizontal que chega na chapa 2 é Bi-engastadas, e a barra vertical que chega na chapa 2 é engastada e apoiada, logo as fórmulas a serem usadas são:
Substituindo certinho temos que:
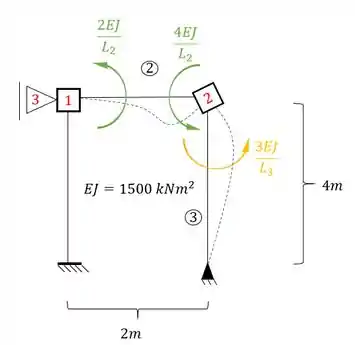
Juntando o que têm-se em cada nó, teremos que:
Perceba que a única barra a dar reação horizontal é a barra 3, sendo assim teremos que:
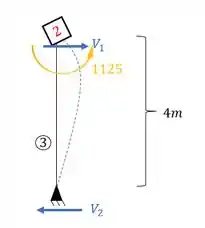
O que podemos admitir para facilitar o cálculo é que o sentido da reação do apoio do primeiro gênero é no mesmo sentido da reação que calculamos na barra, ou seja, se acharmos V1 pra frente, o final é positivo pra frente porque a reação no apoio é positiva pra frente. Logo:
Passo 4
Agora perceba que temos o apoio 3, certo? Nesse caso não rotacionamos, mas deslocamos o nosso apoio de 1 unidade, para podermos determinar os valores de , e .
Quando movimentarmos o apoio, ele afetará TODAS as barras verticais, por isso temos que tomar cuidado, e como se trata de deslocamento e não de rotação, a nossa fórmula será.
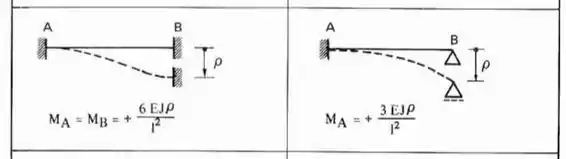
Perceba que a barra vertical da esquerda é Bi-engastada, logo usaremos uma das fórmulas, e para outra que é engasta e apoiada usaremos a outra, sendo assim teremos que:
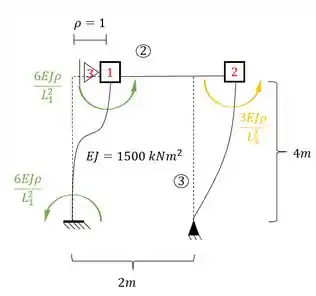
Juntando o que têm-se em cada nó, teremos que:
Perceba que as duas barras produzem reações horizontais que serão armazenadas no nosso apoio do primeiro gênero. Sendo assim teremos que:
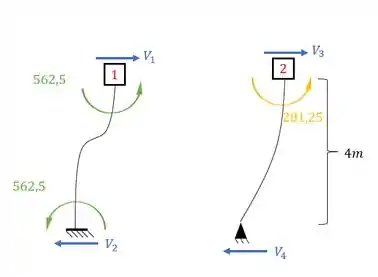
Como V1 e V3 são iguais aos valores das suas respectivas barras, e são as reações na mesma altura no apoio do primeiro gênero, basta somarmos a fazermos o macete de mantermos o sentido da reação calculada, que obtemos que o nosso será dado por:
E assim determinamos todas as rigidezes pedidas.