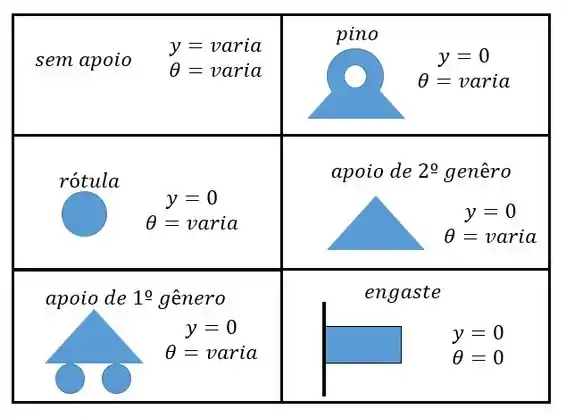
Inclinação e deslocamento por integração
Produzido por Pablo RicardoTeoria
Bom dia, boa tarde, boa noite, boa madrugada, galeraaa!!! Tudo de boinhas com vocês? Espero que sim!
No tópico passado a gente falou um pouco do conceito da linha elástica que é basicamente o diagrama de deflexão de um componente (viga, barra etc..). Se você não viu esse tópico introdutório eu acho que é interessante pelo menos bater o olho lá. É um tópico bem de boas e bem introdutório =D
Dito isso, neste conteúdo aqui vamos abordar como calcular a linha elástica pra valer! Antes a a gente só produziu uns esqueminhas, agora vamos para os números!
A equação da linha estática
Pessoal, vamos pegar o mesmo exemplo do tópico anterior. Então, imagina que uma viga reta, bi apoiada, é submetida a uma força pontual. Como representado abaixo:
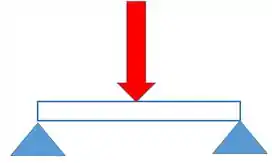
Por causa dessa força a viga vai se deformar da seguinte forma:
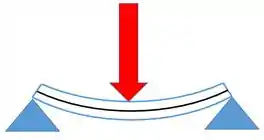
A viga é representada em azul enquanto a linha elástica está em preto. A linha elástica mostra como é a deformação (deflexão) da viga.
Até aqui foi a mesma coisa de antes. Mas eu tenho uma dúvida, quanto vale a flecha no ponto central?
Lembra o que é flecha?
Flecha é a deflexão, a variação em (vertical). É a barriguinha da barra pô! E é isso que vamos calcular, afinal a linha elástica é o diagrama de deflexão, lembram?
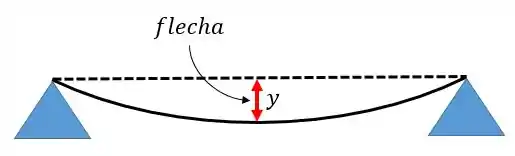
Para isso a gente tem que lembrar da equação do raio de curvatura
Onde:
- é o raio de curvatura.
- é o momento fletor no ponto.
- é a constante de elasticidade.
- é o momento de inércia.
Agora vou mostrar uma parada pra vocês e não se assustem (e digo mais, nem precisam ficar tentando entender muito a equação a seguir não, é mais para vocês saberem de onde vem mesmo. Mas não se preocupem se não entenderem).
Uma curva plana, com raio de curvatura , no eixo pode ser definida como:
Eu avisei...
Mas fiquem tranquilos, vai ficar bem mais fácil porque o termo representa a declividade (o ângulo ). Para refrescar a memória..
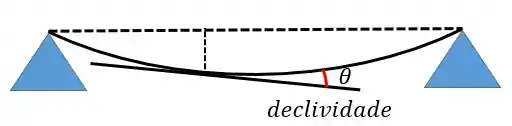
Mas olha só! Para os casos reais esse ângulo é muuuito pequeno. Ou seja, o termo pode ser desprezado e vamos obter:
Como o raio de curvatura era:
Então vamos ter:
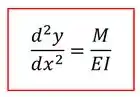
Onde a é a função dalinha elástica e a função que define o momento fletor, ambas em . Podemos dizer que são e , já que são funções.
Pessoal, aqui vai uma observação!! Como, na maioria dos casos, vamos ter diferentes funções de momento para diferentes seções da barra na maior parte das vezes vamos ter que separar o cálculo da linha elástica para cada seção, beleza?
Um exemplo prático
Vamos fazer um exercício para visualizar melhor isso aí!!
Ache a equação da linha elástica para uma viga com um lado engastado e outro livre, com de comprimento. Dado que o momento fletor varia da forma .
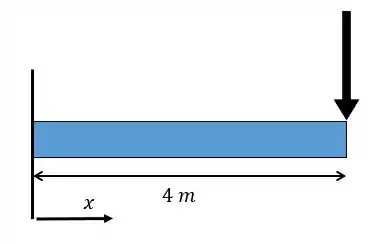
Solução:
Esse exercício já nos dá basicamente tudo e é só utilizarmos a equação da linha elástica.
Substituindo vamos ter:
Agora vamos integrar:
Lembrando que tínhamos uma integral de uma derivada então a ordem da derivada diminui de um grau. E que o termo é uma constante:
Mas quem é ? O termo não igual à declividade ? Então o termo tem a ver com a angulação! Como a viga está engastada em nós vamos aplicar essa condição de contorno. Caso tenha esquecido das condições de contorno..
Para
Assim vamos ter que vale:
Substituindo novamente na equação:
Agora vamos integrar novamente porque queremos o !!
E agora é igual à flecha! Como temos uma posição engastada em então vamos ter que a flecha em ! Substituindo
Assim vamos ter que a equação da linha elástica vale:
Carga e momentos fletores
Pessoal, na maior parte das vezes o problema não vai dar o momento fletor mas vai dar a carga aplicada à viga. A única diferença vai ser vamos ter que calcular o momento fletor antes de aplicar a equação da linha elástica!
Prontos para os exercícios?
Um exemplo prático
Carga e momentos fletores
Exercícios Resolvidos
Exercício Resolvido #1
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 431. Problema 12.3
Determine a equação da linha elástica para a viga utilizando a coordenada válida para . Especifique a inclinação em e a flexão máxima da viga. é constante.
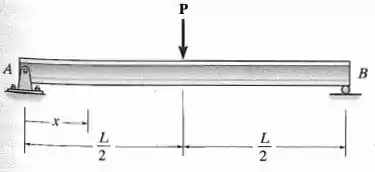
Passo 1
Galera essa questão é bem direta e pede para a gente achar a linha elástica. A gente só tem que achar primeiro o momento fletor antes e aplicar na equação da linha elástica:
Neste exercício é pedido apenas a equação linha estática à esquerda da força (perceba a direção de ).
Passo 2
Para achar o momento fletor primeiro precisamos achar as forças nos apoios, para isso vamos desenhar um esquema de forças.
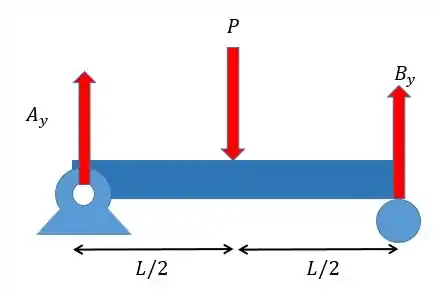
Pelas equações da estática vamos ter:
Para as forças em :
Pessoal, como se trata de um problema simétrico nem precisamos aplicar o somatório dos momentos já que as forças e serão iguais! Sendo assim,
Passo 3
Com as forças vamos poder achar o momento fletor, lembrando que precisamos apenas da metade esquerda. Logo, podemos desenhar o seguinte corte:
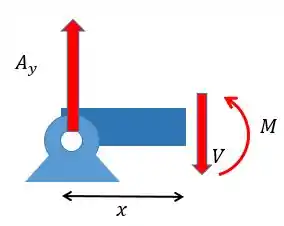
Fazendo o somatório das forças em de modo a achar a força cortante:
Agora podemos achar o momento fletor, fazendo o somatório dos momentos em torno do ponto e considerando o sentido horário positivo:
Uhulll achamos o momento!! Agora vamos achar a linha elástica!!
Passo 4
Para achar a linha elástica a gente só precisa daquela equação com uma derivada de segunda ordem:
Substituindo :
Agora vamos integrar em :
Mas pessoal, se liga na sacada mestre!!!
Como temos um problema simétrico, então no ponto central da viga vamos ter que , a inclinação, vale zero!!
Sendo assim podemos substituir na equação acima para achar :
Então temos:
E podemos integrar novamente para achar :
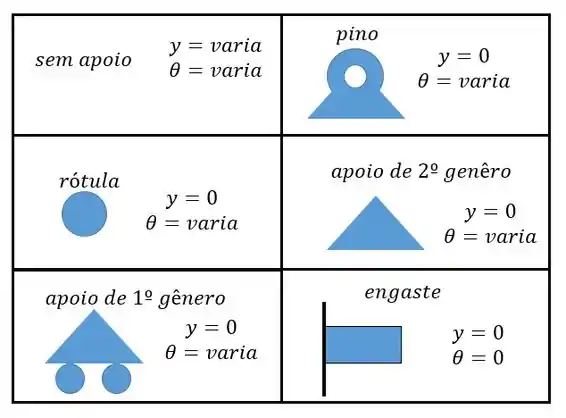
Agora vamos utilizar as condições de contorno para achar as contantes, olhando a nossa tabelinha a gente percebe que temos de utilizar as seguintes condições:
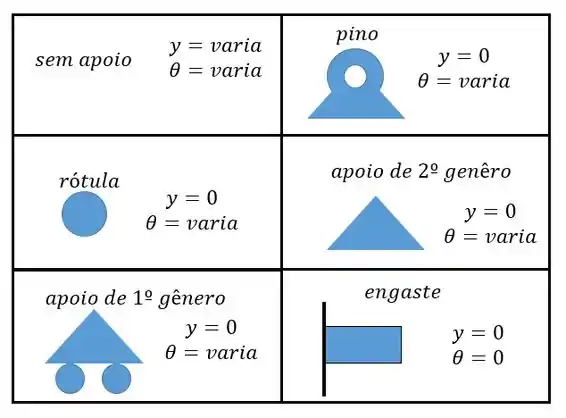
Como o pino se encontra em é só substituir e achar:
Logo,
Então a equação que temos é a seguinte:
Que pode ser expressa como:
Já temos a primeira parte do problema que é a linha elástica.
Passo 5
Agora vamos calcular a inclinação em , como a inclinação é dada pela equação:
É só substituir
A deflexão máxima ocorre no ponto central (pelo motivo de simetria) e vai ser dada por:
Substituindo
Resposta
Exercício Resolvido #2
Elaboração própria
Uma viga engastada está sujeita a uma força conforme o desenho abaixo. Considerando constante encontre a equação da linha elástica. Encontre também a máxima deflexão e inclinação.
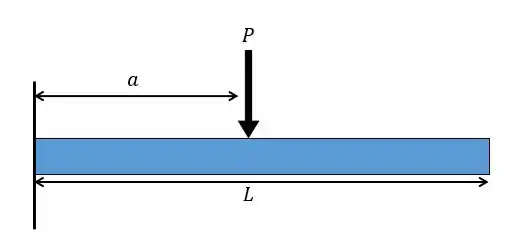
Passo 1
A gente tem que achar a linha elástica e para isso precisamos achar primeiro o momento fletor antes e aplicar na equação da linha elástica:
Lembrando que temos de utilizar as condições de contorno dadas por aquela nossa tabelinha:
Passo 2
Para achar o momento fletor primeiro precisamos achar as forças nos apoios, para isso vamos desenhar um esquema de forças.
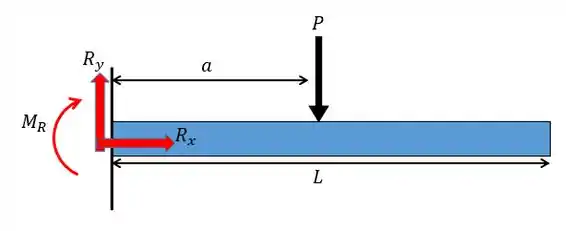
Pelas equações da estática vamos ter:
Como só existe uma força em :
Para as forças em :
Para os momentos considerando o sentido horário positivo e aplicados na extremidade engastada vamos ter:
Passo 3
Com as forças vamos poder achar o momento fletor, realizando um corte entre o engaste e a aplicação da força vamos ter:
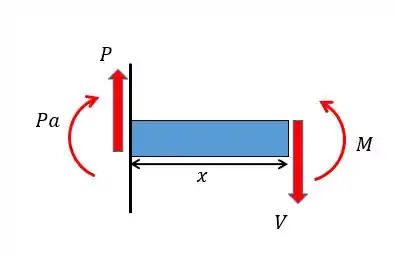
Fazendo o somatório das forças em de modo a achar a força cortante:
Agora podemos achar o momento fletor, fazendo o somatório dos momentos em torno do ponto e considerando o sentido horário positivo:
Uhulll achamos o momento!! Agora vamos achar a linha elástica!!
Passo 4
Para achar a linha elástica a gente só precisa daquela equação com uma derivada de segunda ordem:
Substituindo :
Agora vamos integrar em :
Agora podemos utilizar a condição de contorno referente ao ângulo (porque ). Com isso vamos ter que a inclinação em (no ponto de engaste) é nula. Se quiser volta lá na tabelinha pra conferir =D
Substituindo os valores vamos ter:
Logo,
Nossa equação fica da forma:
Com isso já da para achar a maior inclinação. Podemos perceber que essa função é estritamente crescente, sendo assim o maior valor da inclinação ocorrerá no maior ponto de ou seja :
Passo 5
Agora vamos derivar a equação novamente para achar a linha elástica:
Como no engaste () não temos deflexão vamos ter:
Sendo assim
E a equação da linha elástica é dada por:
Passo 6
Da mesma forma que a inclinação, a linha elástica vai ser estritamente crescente. Sendo assim, vamos ter o maior valor em obtendo:
Resposta
Exercício Resolvido #3
Elaboração própria
Uma viga engastada está sujeita a uma carga conforme o desenho abaixo. Considerando constante encontre a equação da linha elástica.
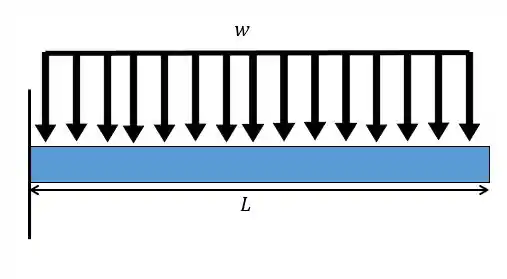
Passo 1
Pessoal esse problema é muito parecido com o anteior e a gente tem que achar a linha elástica também. Para isso, como sabemos, precisamos achar primeiro o momento fletor antes e aplicar na equação da linha elástica:
O que vai mudar aqui vai ser a forma de calcular o momento fletor, vamos fazer isso por meio de integral!
Lembrando que temos de utilizar as condições de contorno dadas por aquela nossa tabelinha:
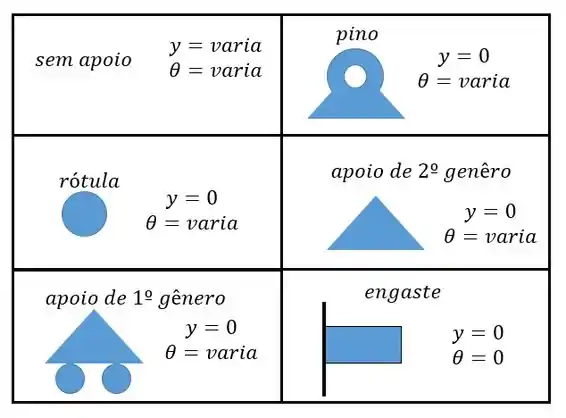
Passo 2
Galera, vocês devem lembrar que a força cortante é a derivada do momento fletor. Se não lembravam agora vocês sabem =P
Além disso, a carga distribuída é a derivada da força cortante. Então a gente tem o seguinte olha só:
Esse sinal de menos é muito importante ok? Não podemos esquecer! Ele aparece porque a cortante tem o sentido oposto do carregamento.
Então, a gente pode falar que:
Né? É só derivar o momento fletor duas vezes que vamos ter a carga.
Mas pessoal a equação da linha elástica não é dada por:
Então a gente pode derivar duas vezes e vamos ter:
Agora podemos substituir o termod a direita pelo carregamento e obter:
Desta forma podemos achar a linha elástica diretamente do carregamento
Passo 3
Aplicando esse conceito ao problema vamos ter:
Podemos reorganizar da forma:
Aí é só ir derivando rs. A primeira derivada temos:
Derivando novamente:
Derivando pela terceira vez:
Derivando pela quarta e última vez:
Agora é “só” achar as quatro constantes rs

Passo 4
Pessoal, para achar essas constantes a gente tem que reparar que cada uma delas, por estar associada a cada etapa de integração, vai estar associada aos termos da força cortante, momento fletor, inclinação e deflexão.
Vamos um pouco mais devagar. Lá na primeira integral a gente tinha:
O termo da esquerda é a primeira integral de logo é igual à força cortante e podemos escrever:
Logo se a gente conseguir achar a força cortante em algum ponto da nossa viga vamos poder achar !
Na extremidade livre não temos força cortante, portanto:
Tranquilo né?
Passo 5
Agora vamos para a segunda integral, já considerando o valor de :
Essa integral se refere ao momento fletor e pode ser escrita como:
Vamos aplicar o mesmo conceito e, ao perceber que também não existe momento fletor na extremidade livre, vamos obter:
Passo 6
Agora vamos para a terceira integral, já considerando os valores de e :
Essa integral se refere à inclinação e pode ser escrita como:
Vamos aplicar o mesmo conceito mas agora temos de utilizar o lado engastado, porque no engaste a inclinação é zero. Temos, portanto:
Passo 7
Agora vamos para a quarta integral, já considerando os valores de , e :
Essa integral se refere à linha elásticae pode ser escrita como:
Vamos aplicar o mesmo conceito mas agora temos de utilizar o lado engastado, porque no engaste a deflexão também é zero. Temos, portanto:
Logo a equação da linha elástica é igual a:
Que pode ser escrita como:
Resposta
Exercício Resolvido #4
Ferdinand P. Beer, E. Russell Johnston, Resistência dos Materiais, 3ª ed. São Paulo: MAKRON BOOKS, 1995, pp. 846. Exercício 8 – 20 (Adaptada)
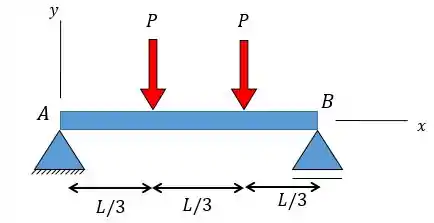
Sabendo-se que a viga é um perfil laminado de aço e que , e , determinar a declividade em .
Passo 1
Essa questão é bem direta e pede para a gente achar a linha elástica. A gente só tem que achar primeiro o momento fletor antes e aplicar na equação da linha elástica:
Neste exercício é pedido apenas a equação linha estática à esquerda da força (perceba a direção de ).
A diferença aqui é que no final vamos substituir os valores para achar um resultado numérico ao invés de um resultado estilo “sopa de letrinhas”.
Passo 2
Galera, como o foco da aula é a linha elástica eu já vou colocar aqui para vocês o resultado das reações e do momento fletor:
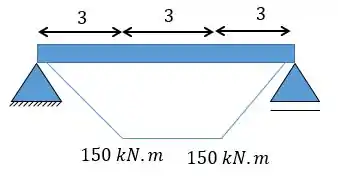
Então a equação do momento fletor pode ser dividida em três partes e será:
- Para
- Para
- Para
- Para
- Para
Passo 3
Para achar a linha elástica a gente só precisa daquela equação com uma derivada de segunda ordem:
Pessoal! Como a gente quer só a declividade em podemos pegar apenas a primeira parte:
Substituindo :
Agora vamos integrar em :
Show de bola! Essa vai ser a equação da nossa angulação, mas a gente ainda precisa encontrar o valor de , vamos fazer isso utilizando a seção do meio.
Passo 4
Para a seção do meio nós vamos ter:
Substituindo na equação:
Agora temos a equação da angulação para a seção do meio, e por que fizemos isso? Porque agora podemos achar o valor de , já que sabemos que a inclinação exatamente na metade é igual a zero (porque a viga é simétrica)!
Assim, vamos ter:
Passo 3
Mas a gente não quer a inclinação em ? Então vamos igualar a equação da primeira parte e da segunda parte no ponto onde elas devem ser necessariamente iguais, em !!
Primeira parte:
Segunda parte:
Igualando as duas em :
Agora é só substituir na equação da primeira parte:
Passo 4
Com isso vamos ter:
Como queremos em
E substituindo o valor de fornecido no problema e fornecido nas tabelas de perfis de abas largas, vamos ter:
Resposta
Exercício Resolvido #5
Ferdinand P. Beer, E. Russell Johnston, Resistência dos Materiais, 3ª ed. São Paulo: MAKRON BOOKS, 1995, pp. 844. Exercício 8 - 5
Para o carregamento mostrado, determinar: (a) a equação da curva elástica para a viga ; (b) a deflexão da extremidade livre; (c) a declividade da extremidade livre. Assuma constante.
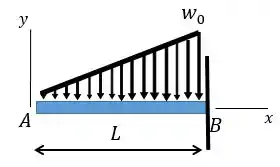
Passo 1
Fala, galerinha!!! Aqui o problema nos fornece uma viga engastada em e livre em e submetida a um carregamento triangular conforme mostrado. Como existe um carregamento distribuído a gente pode utilizar direto a equação que relaciona carregamento com deflexão:
Dessa forma o mais importante para a gente agora é encontrar a função que define o carregamento e definir o sentido do eixo .
Passo 2
Primeiro vamos definir o sentido do eixo , essa parte é muito importante ok? A nossa questão até já deixou meio indicado mas vou mostrar para vocês qual foi adotado:
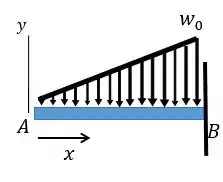
Ou seja, vamos varrer nossa viga da esquerda para a direita.
Para definir a função do carregamento a gente só precisa lembrar que essa é uma função linear que se inicia no ponto e termina em , com isso vamos obter:
Perceba que o valor de é, por exemplo:
Faz sentido né?
Passo 3
Agora vamos resolver a integral:
Substituindo
Integrando a primeira vez:
Se escrevermos da seguinte forma vamos ter o valor da força cortante:
Com isso podemos achar o valor da constante pois a força cortante no ponto é zero. Logo,
Passo 4
Continuando a resolução da equação e fazendo a segunda integral:
E vamos obter:
Novamente vamos poder escrever como algo que conhecemos que é o momento fletor:
E novamente o momento fletor em é igual a zero, logo:
Passo 5
Agora vamos integrar pela terceira vez:
Agora a gente tem que lembrar que o termo é igual à angulação . Assim, podemos escrever:
Não sabemos qual a angulação da extremidade livre, mas sabemos qual é a angulação da extremidade engastada (que é zero). Logo podemos substituir e :
Como o problema também pede a inclinação na extremidade livre podemos fazer e obter:
Passo 6
Agora vamos para a nossa quarta e última integral:
E finalmente achamos a equação da linha elástica:
Mas ainda falta achar o valor de e para isso utilizamos o valor da deflexão no engaste, que é zero. Logo:
E finalmente obtemos a equação da linha elástica:
Para achar a deflexão na extremidade livre é só substituir
Pronto! Problema resolvido =D
Resposta
a)
b)
c)
Exercício Resolvido #6
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 433. Problema 12.19
Determine a equação da linha elástica para a viga utilizando as coordenadas e e especifique a inclinação em . é constante.
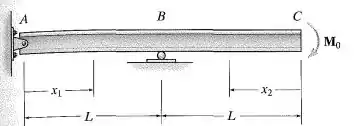
Passo 1
Pessoal, nada de novo no horizonte. O problema pede a equação da linha elástica e a inclinação em , . Para tal a gente vai precisar da nossa equaçãozinha:
E como na maior parte das vezes vamos calcular o momento fletor na viga =D
Passo 2
Para achar o momento fletor primeiro precisamos achar as forças nos apoios, para isso vamos desenhar um esquema de forças.
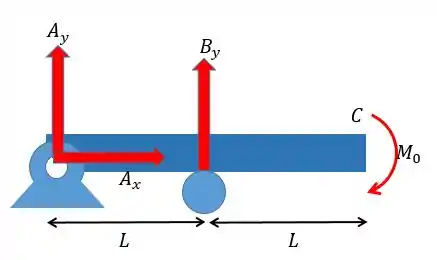
Pelas equações da estática vamos ter:
Como só temos uma força em vamos ter:
Para as forças em :
Para o momento sendo aplicado em e considerando positivo o sentido horário vamos ter:
Da equação em a gente pode achar que:
Passo 3
Com as forças vamos poder achar o momento fletor. Desenhando o corte da primeira seção vamos ter:
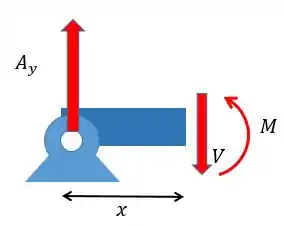
Fazendo o somatório das forças em de modo a achar a força cortante:
Agora podemos achar o momento fletor, fazendo o somatório dos momentos em torno do ponto e considerando o sentido horário positivo:
Uhulll achamos o momento!! Agora vamos achar a linha elástica!!
Passo 4
Para achar a linha elástica a gente só precisa daquela equação com uma derivada de segunda ordem:
Substituindo :
Agora vamos integrar em :
Integrando novamente vamos ter:
Agora temos de utilizar as condições de contorno para obter e .
Passo 5
Lembrando que as condições são as seguintes:
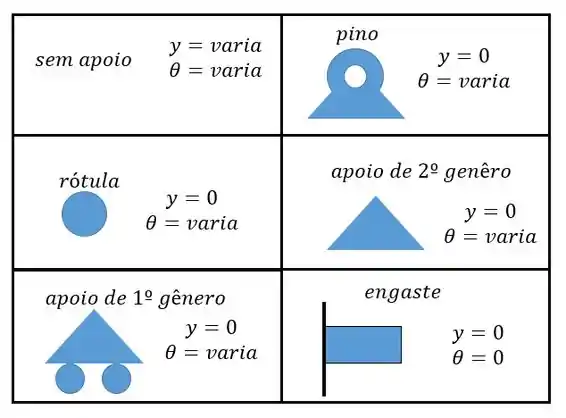
Ao aplicar essas condições no pino () vamos ter um :
Logo,
Portanto a equação fica da forma:
Agora vamos aplicar na rótula em onde , nesse ponto a deflexão também é zero, logo:
Então a equação da linha elástica é igual a:
Que pode ser escrita como:
Passo 6
Para achar a inclinação em basta utilizar a equação da inclinação lembrando que :
Em então vamos ter:
Passo 7
O problema também pediu para acharmos a equação da linha elástica ao lado direito da rótula. Isso faz sentido porque a equação que achamos é válida apenas para o trecho entre o pino e a rótula.
Para fazer isso vamos desenhar um corte dessa seção:
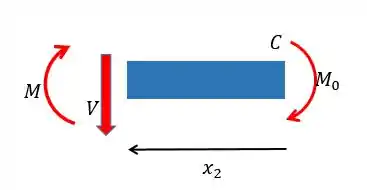
Olhando esse desenho prodemos perceber que existe apenas uma força, logo ela é nula. Assim
Com relação aos momentos, para que o corpo permaneça em equilíbrio ele deve ter os momentos iguais em módulo mas sentido opostos:
Tranquilo né? O momento fletor desse trecho é igual ao próprio momento puro aplicado só que no sentido oposto.
Passo 8
Agora é só utilizar a equação da linha elástica:
Derivando uma vez vamos ter:
Derivando novamente:
Agora só precisamos achar as contantes.
Passo 9
Deste lado da viga temos apenas uma condição de contorno. A condição de que não há deflexão no ponto onde sendo assim:
Mas ainda temos duas incógnitas e uma equação, então como vamos proceder?
Na verdade temos mais uma condição de contorno sim, só que está implícita num princípio da continuidade.
Ou seja, se calcularmos a inclinação em por meio da seção esquerda da viga, essa inclinação deve ser igual à calculada pelo lado direito!!
Sendo assim vamos ter, do lado esquerdo:
Lembrando que e substituindo os valores de vamos obter:
Agora se fizermos para a seção do lado direito:
Substituindo
Como os dois valores de são iguais:
Agora podemos substituir lá na equação:
Finalmente podemos substituir na equação da linha elástica:
É possível até verificar substituindo e verificando que =D
Resposta
Exercício Resolvido #7
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 432. Problema 12.12
Determine a deflexão em da barra. Considere constante.
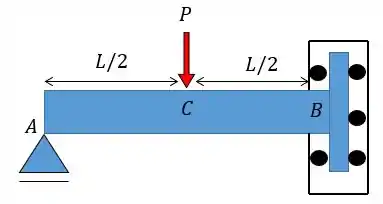
Passo 1
Fala, galerinha!!! Aqui o problema nos fornece uma viga apoiada num apoio de primeiro gênero na extremidade esquerda e com um apoio do tipo carrinho na extremidade direita. Devemos lembrar que esse tipo de apoio impede tanto a rotação quanto o deslocamento na horizontal porém permite o deslocamento na vertical. Então as nossas reações vão ficar assim:
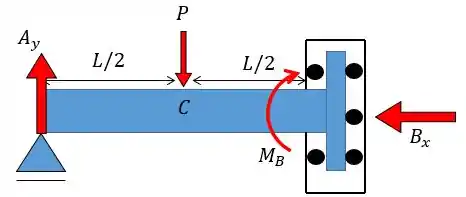
Com isso o principal é achar a função que defini o momento fletor na barra para podermos substituir na equação da linha elástica:
Passo 2
Primeiro vamos definir o sentido do eixo , essa parte é muito importante ok? Então podemos definir por exemplo da esquerda para a direita:
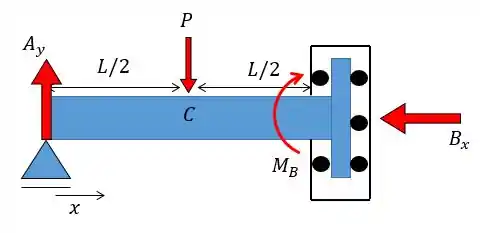
Como só existe uma força na horizonta então vamos ter que:
Logo, para as forças no eixo vertical vamos ter:
E para as momentos, aplicados em , vamos ter:
Pronto! Achamos nossas reações, agora montar o diagrama de momentos fletores ficou mais fácil:
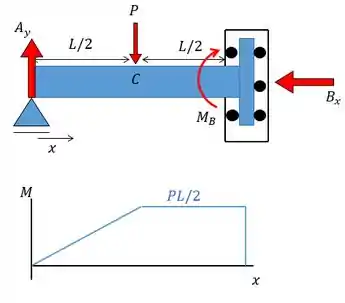
Desta forma vamos ter a função do momento fletor dada por:
Passo 3
Agora vamos partir para as integrais, lembrando que temos duas equações de momento fletor, então devemos fazer cada uma separadamente. Vamos começar com o lado esquerdo:
Substituindo
Integrando novamente:
Então para a primeira metade temos:
obs: Lembre-se que
Passo 4
Agora vamos fazer para o lado direito:
Substituindo:
Integrando novamente:
Agora também temos as duas equações do lado direito:
Falta achar só as constantes! Para isso vamos utilizar as condições de contorno.
Passo 5
A primeira condição de contorno e a mais simples de ser observada é que não há deflexão no ponto , dessa forma podemos substituir na seguinte equação:
E obter:
A segunda condição de contorno que é um pouco mais difícil de ser observada é que, o apoio do lado impede a rotação, logo podemos substituir no ponto da seguinte equação:
Substituindo:
Show de bola, mas agora acabaram as nossas condições de contorno, o que faremos?
Passo 6
No problema nós temos apenas uma barra, contínua, mas na nossa resolução nós temos o dobro de equações. Como a barra é contínua nós podemos dizer que a inclinação e deflexão do ponto será igual independetemente da equação que estamos olhando.
Dessa forma nós vamos ter que as equações das inclinações e das deflexões são iguais..
Mas é importante lembrar que isso só vale para , então vamos substituir:
Substituindo as constante que a gente já calculou:
Vamos obter:
Agora temos um sistema com duas equações e duas incógnitas, resolvendo nós vamos achar:
Passo 7
Então nossa equação da deflexão para a segunda metade é dada por:
Substituindo obtemos:
Resposta
Exercício Resolvido #8
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 433. Problema 12.27
Determine a linha elástica para a viga simplesmente apoiada utilizando a coordenada onde . Determine também a inclinação em e a deflexão máxima da viga. é constante.
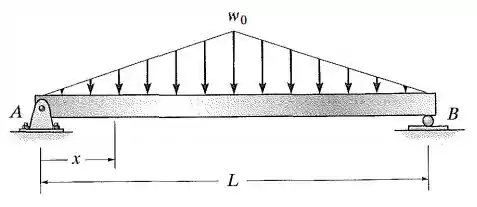
Passo 1
Nesta questão a gente tem que achar a linha elástica, a forma mais fácil para esse tipo de problema, que nos fornece o carregamento é realizar como:
Passo 2
Então o primeiro problema que encontramos é definir o carregamento como uma função em . Esse carregamento é triangular e, portanto, aumenta linearmente. Logo, pode ser descrito como:
Como o valor inicial do carregamento é igual a zero, então o termo .
Agora se aplicarmos essa função no ponto vamos obter o valor de , assim:
Sendo assim,
E o nosso carregamento pode ser dado por:
Passo 3
Agora vamos aplicar a equação da linha elástica:
Podemos reorganizar da forma:
Aí é só ir derivando rs. A primeira derivada temos:
Derivando novamente:
Derivando pela terceira vez:
Derivando pela quarta e última vez:
Agora é só achar as quatro constantes!
Passo 4
Pessoal, para achar essas constantes a gente tem que reparar que cada uma delas, por estar associada a cada etapa de integração, vai estar associada aos termos da força cortante, momento fletor, inclinação e deflexão.
Vamos um pouco mais devagar. Lá na primeira integral a gente tinha:
O termo da esquerda é a primeira integral de logo é igual à força cortante e podemos escrever:
Logo se a gente conseguir achar a força cortante em algum ponto da nossa viga vamos poder achar !
A cortante num ponto bem próximo de vai ser igual à própria reação em . Podemos calcular a reação em como sendo metade da força aplicada sobre a viga.
Como essa força é dada pela carga distribuída, vamos ter:
Pessoal, reparem que eu peguei só a força do triângulo da esquerda (carga vezes distância). Por que eu fiz isso? Porque queria metade da força uai!
Então para vamos ter:
Logo,
Passo 5
Agora vamos para a segunda integral, já considerando o valor de :
Essa integral se refere ao momento fletor e pode ser escrita como:
O momento fletor num ponto bem próximo do apoio será igual a zero, portanto:
Passo 6
Agora vamos para a terceira integral, já considerando os valores de e :
Essa integral se refere à inclinação e pode ser escrita como:
Agora temos de utilizar aquela propriedade de que o ângulo no ponto médio de uma viga com carregamento simétrico é nulo! Portanto em vamos ter . Assim,
Passo 7
Agora vamos para a quarta integral, já considerando os valores de , e :
Essa integral se refere à linha elástica!!
Vamos aplicar a condição de contorno onde a deflexão no apoio é nula, logo em temos que . Portanto,
Desta forma vamos ter que a linha elástica é dada por:
Que pode ser escrito como: