Determine o atrito entre a caixa de 50kg e o piso se a) e b) . Os coeficientes de atrito estático e cinético entre a caixa e o piso são e , respectivamente.
Passo 1
E aí, pessoal! Tudo certinho?

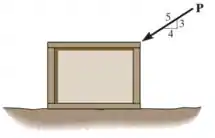
Nesse problema temos uma caixa de e age sobre ele uma força .
Foi dito que os coeficientes de atrito entre a caixa e o piso é (estático) e (cinético) .
A partir daí temos que determinar a força de atrito entre o piso e a caixa se e se .
Parece complicado?
Para resolver esse problema temos que usar a segunda lei de Newton:
E para um corpo parado, temos
Em cada um dos casos temos que verificar se a força de atrito é suficiente para segurar a caixa... pra descobrir essa força, temos que lembrar da fórmulinha
Lembrando que não é horizontal, então sua componente vertical vai influenciar em .
Bora começar!
Passo 2
A primeira coisa que vamos fazer é buscar uma expressão para a força de atrito máxima.
Nesse caso, a normal vai ser a soma da força peso com a componente vertical da força (pois o sistema está em equilíbrio verticalmente).
A força peso é:
Se e , temos:
A força é mostrada na figura do enunciado:
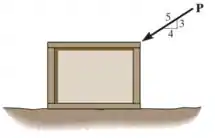
Para encontrar sua componente vertical fazemos:
Portanto, pela segunda lei de Newton, temos que a força normal é:
Logo, a força de atrito máxima é expressa como:
Tranquilo até aqui?
Passo 3
Agora, vamos verificar o que acontece se .
Nesse caso, a força de atrito máxima é :
Agora temos que comparar essa força com a componente horizontal da força .
Nesse caso, temos que , logo, a força aplicada não é suficiente para mover a caixa e nem para exigir a força máxima de atrito.
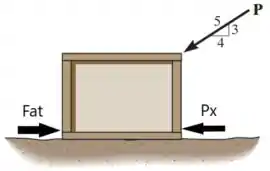
Pela segunda lei de Newton, temos que:
Ou seja:
Tranquilo?
Passo 4
Agora vamos analisar o que acontece quando .
Nesse caso, a força de atrito máxima é:
Comparando essa força com a força horizontal , temos:
Aqui a situação é justamente a contrária... , ou seja, o bloco passa a se mover pois a força de atrito já não é mais capaz de segurar o bloco.
Nesses casos, a força de atrito então será a força de atrito cinética .
É isso! Sacou como faz? Responde Aí!
Resposta
a)
b)