Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 119
119- Cada uma das estruturas mostradas nas figuras consiste em dois elementos em forma de ligados por duas hastes rígidas. Para cada estrutura, determine as reações nos apoios e indique se a estrutura é rígida.
Passo 1
Os elementos representados em e podem ser separados pelos cabos de forma que temos o sistema de forças em .
Onde o ângulo formado entre as cordas tem os seguintes valores de seno e cosseno.
Fazendo a somatória dos momentos em (considerando o sentido horário como positivo) na estrutura da direita nós temos:
Fazendo agora o momento em pela estrutura a esquerda nós temos:
Substituindo a relação de com nós teremos:
Isso nos dá:
Isso nos dá uma força igual a:
Passo 2
Dessa forma pela somatória de todas as forças nós temos:
E somatória das forças verticais iguais a:
Sistema rígido, pois conseguimos encontrar todas as forças sem nenhuma incongruência ou um que desestabilizaria a estrutura.
Passo 3
Agora para a letra .
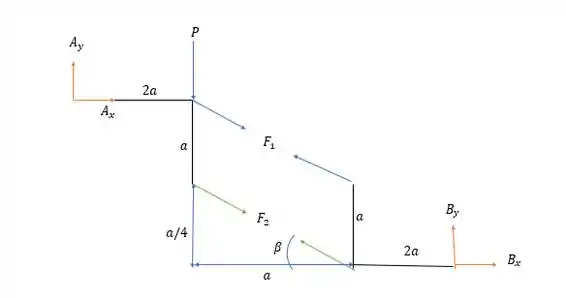
Fazendo a somatória dos momentos em ser zero na estrutura a direita dos cabos nós temos:
Agora fazendo a somatória dos momentos em na estrutura a esquerda dos cabos:
Só que como , logo o que nos dá em:
O que nos dá em uma estrutura não rígida, uma vez que somente não existindo para estrutura ficar no lugar.
Passo 4
O diagrama de forças para a letra .
Mesmo procedimento, vamos fazer a somatória dos momentos em .
Agora a somatória dos momentos em na estrutura a esquerda dos cabos nos dá:
Aplicando a substituição nós temos:
Logo dará:
Passo 5
Aplicando a somatória das forças nós temos:
E a somatória das forças verticais nas duas estruturas nos dará:
Como conseguimos encontrar todas as reações em relação a sem problema algum e sem encontrar nada que dê , logo a estrutura é rígida.