Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 50

18.49. Determine a energia cinética do paralelepípedo sólido do Problema 18.7

Passo 1

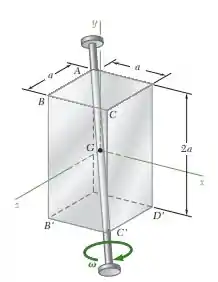
Vamos começar esse problema lembrando do 18.7. Naquele problema a gente tinha um paralelepípedo retangular sólido com massa m girando a uma velocidade ω em torno da sua diagonal girando no sentido anti-horário.

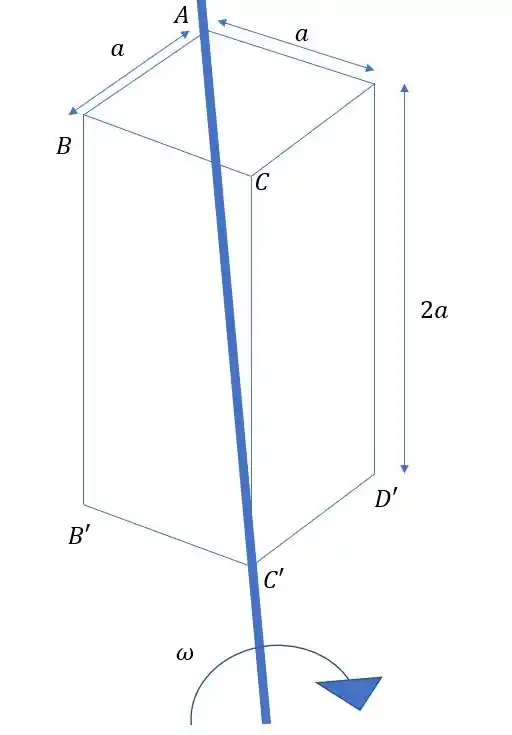
A gente pode calcular a diagonal principal assim

D = a 2 + 2 a 2 + a 2 = 6   a

E a área total do paralelepípedo é o seguinte

A = 2 a 2 + 4 2 a ⋅ a = 10 a 2

Passo 2

Agora vamos dar uma olhada em ω . A gente pode decompor o vetor ω → .

ω → = ω   - a D   i ^ + ω   2 a D   j ^ + ω   - a D   k ^

Então

ω → = - ω 6   i ^ + 2 ω 6   j ^ - ω 6 k ^

Passo 3

Agora vamos calcular os momentos de inércia. Como o paralelepípedo é oco nesse problema, o melhor que podemos fazer é separar por planos. No plano x z nós temos dois quadrados, o de cima e o de baixo. Cada quadrado tem um décimo do peso do paralelepípedo completo.

m x z = 1 10 m

A gente pode dizer isso porque o paralelepípedo é homogêneo, e a área de um quadrado é um décimo da área do paralelepípedo.

Nesse plano vamos calcular:

I x = 1 12 m x z a 2 + m x z a 2 = 13 12 m x z a 2 = 13 120 m a 2

Para o eixo y

I y = 1 6 m x z a 2 = 1 60 m a 2

E agora para o eixo z podemos usar a simetria do problema

I x = I z = 13 120 m a 2

Agora vamos para outro plano, o plano y z . Vamos seguir o mesmo raciocínio. Nesse plano vamos ter dois retângulos, cada retângulo possui 2 10 , ou 1 5 , da massa do paralelepípedo.

m y z = 1 5 m

Então

I x = 1 12 m y z a 2 + 1 12 m y z 2 a 2 = 5 12 m y z a 2 = 1 12 m a 2

E para o eixo y

I y = 1 12 m y z a 2 + m y z a 2 2 = 1 3 m y z a 2 = 1 15 m a 2

E por último

I z = 1 12 m y z 2 a 2 + m y z a 2 2 = 7 12 m y z a 2 = 7 60 m a 2

E agora o último plano que vamos analisar é o plano que vamos analisar é o plano x y , que é bem parecido com o plano y z , vamos ter 2 retângulos.

Então

I x = 1 12 m x y 2 a 2 + m x y a 2 2 = 7 12 m x y a 2 = 7 60 m a 2

E para o eixo y

I y = 1 12 m y z a 2 + m y z a 2 2 = 1 3 m y z a 2 = 1 15 m a 2

E por último

I z = 1 12 m x y a 2 + 1 12 m x y 2 a 2 = 5 12 m x y a 2 = 1 12 m a 2

Agora a gente só precisa somar tudo.

I x = 13 120 m a 2 + 1 12 m a 2 + 7 60 m a 2 = 37 60 m a 2

I y = 1 60 m a 2 + 1 15 m a 2 + 1 15 m a 2 = 3 10 m a 2

I z = 13 120 m a 2 + 7 60 m a 2 + 1 12 m a 2 = 37 60 m a 2

Passo 4

Agora só precisamos calcular a cinética.

T = 1 2 m v - 2 + 1 2 I x ω x 2 + 1 2 I y ω y 2 + 1 2 I z ω z 2

O eixo de rotação passa pelo centro de gravidade, então

v - = 0

Agora vamos substituir os valores

T = 0 + 1 2 37 60 m a 2 ω 6 2 + 1 2 3 10 m a 2 2 ω 6 2 + 1 2 37 60 m a 2 ω 6 2

Resolvendo isso aqui fica

T = 73 360 m a 2 ω 2

Resposta

T = 73 360 m a 2 ω 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A lixadeira mostrada na figura está inicialmente em repouso. Se o tambor de acionamento B tem uma aceleração angular constante de 120r a d/ s 2 no sentido anti-horário, determine a intensidade da acel
Uma placa circular de raio 250m m mostrada na figura está inicialmente em repouso e tem a aceleração angular definida pela relação α = α 0 cos ⁡ ( π t / T ) . Sabendo que T = 1,5s e α 0 = 10r a d/ s 2
O anel C tem uma raio interno de 55 mm e um raio externo de 60 mm e é posicionado entre duas rodas A e B, cada uma com raio externo de 24 mm. Sabendo que a roda A gira com uma velocidade angular const
A velocidade nominal do tambor B da lixadeira mostrada na figura é de 2.400 rpm. Quando a lixadeira é desligada, observa-se que o tambor, então livre, alcança o repouso em 10 s. Admitindo-se um movime
Uma corda é enrolada em torno de um cilindro de raio r e massa m, conforme mostrado. Sabendo que o cilindro foi solto do repouso, determine a velocidade do centro do cilindro após ele ter se movido pa