Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 57

18.57. Determine a taxa de variação A da quantidade de movimento angular HA da placa do Problema 18.3, sabendo que sua velocidade angular permanece constante

Passo 1

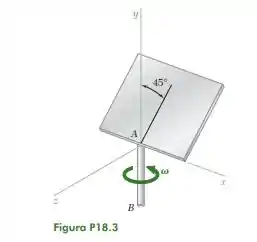
Vamos começar relembrando o problema 18.3. No problema temos uma placa homogênea que forma um ângulo de 45° com uma barra vertical A B - . O eixo A B - gira com uma velocidade ω → = ω   j ^ .

Agora podemos começar a resolver o problema. O primeiro passo que vamos dar é usar os eixos y ' e z ' , em que z ' é o eixo normal a placa e y ' é o eixo que está no plano da placa e é ortogonal ao eixo x .

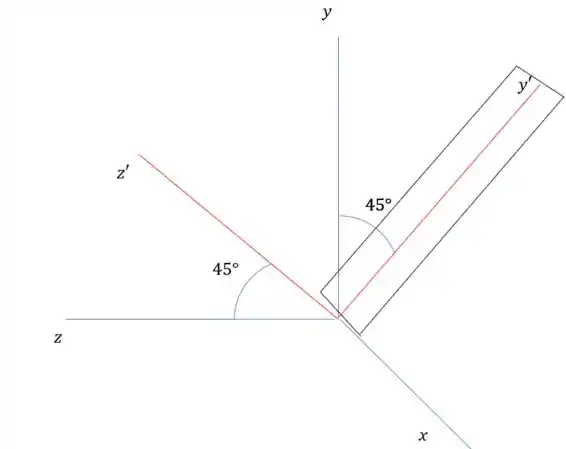
Nesse desenho as linhas pretas representam a placa.

Podemos colocar ω → nas novas coordenadas.

ω x = 0 ω y ' = ω cos ⁡ 45 ° ω z ' = ω sin ⁡ 45 °

Passo 2

Vamos calcular os momentos de inercia.

I x = 1 3 m a 2

Onde a a é o tamanho de um lado da placa.

I y ' = 1 12 m a 2

E por último

I z ' = I x + I y ' = 1 3 m a 2 + 1 12 m a 2 = 5 12 m a 2

Passo 3

Agora a gente tem tudo para calcular o momento angular:

H → A = I x ω x   i ^ + I y ' ω y '   j ^ ' + I z ' ω z '   k ^ '

Substituindo os valores

H → A = 1 3 m a 2 ( 0 )   i ^ + 1 12 m a 2 ω cos ⁡ 45 °   j ^ ' + 5 12 m a 2 ω sin ⁡ 45 °   k ^ '

Então

H → A = 1 12 m a 2 ω cos ⁡ 45 °   j ^ ' + 5 12 m a 2 ω sin ⁡ 45 °   k ^ '

H A → = 1 12 m a 2 ω cos ⁡ 45 °   j ^ ' + 5 sin ⁡ 45 °   k ^ '

A gente pode voltar para os eixos cartesianos. Se você olhar bem para a figura que desenhamos lá no começo você consegue ver que

j ^ ' = cos ⁡ 45 °   j ^ - sin ⁡ 45 °   k ^

k ^ ' = sin ⁡ 45 °   j ^ + cos ⁡ 45 °   k ^

Vamos fazer a imagem no plano y z para ficar mais fácil de enxergar isso.

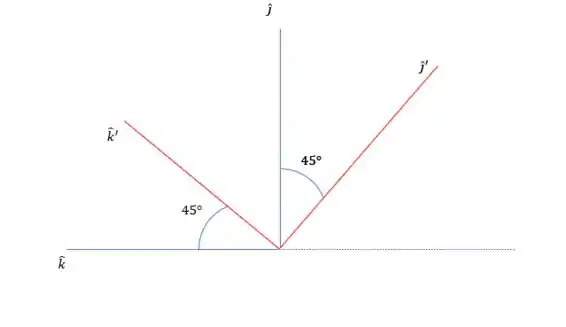Então vamos fazer

H A → = 1 12 m a 2 ω ⋅ cos ⁡ 45 °   cos ⁡ 45 °   j ^ - sin ⁡ 45 °   k ^ + 5 sin ⁡ 45 ° sin ⁡ 45 °   j ^ + cos ⁡ 45 °   k ^

Lembre-se que cos 2 ⁡ 45 ° = sin 2 ⁡ 45 ° = cos ⁡ 45 ° sin ⁡ 45 ° = 1 2 , isso vai ajudar aqui

H A → = 1 12 m a 2 ω ⋅ 1 2   j ^ - 1 2   k ^ + 5 ⋅ 1 2   j ^ + 5 ⋅ 1 2 k ^

Isso fica

H A → = 1 12 m a 2 ω ⋅ 3   j ^ + 2   k ^

Passo 4

Agora vamos podemos calcular H → ˙ A , e isso não vai ser tão complicado nesse problema, porque ω é constante, então

H → ˙ A x y z = 0

E também podemos assumir

Ω → = ω → = ω   j ^

Então

H → ˙ A = H → ˙ A x y z + Ω → × H A →

É a mesma coisa que

H → ˙ A = ω → × H A →

Vamos substituir os valores

H → ˙ A = ω   j ^ × 1 12 m a 2 ω ⋅ 3   j ^ + 2   k ^

Isso aqui fica

H A → ˙ = 1 6 m a 2 ω 2   i ^

E terminamos mais um problema.

Resposta

H A → ˙ = 1 6 m a 2 ω 2   i ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas hastes estreitas idênticas AB e BC são soldadas para formar um conjunto em forma de L. O conjunto é pressionado contra uma mola em D e liberado da posição mostrada. Sabendo que o ângulo máximo de
O movimento da haste AB de 10 kg delgada é guiado por colares de massa desprezível que deslizam livremente nas hastes verticais e horizontais mostradas. Sabendo que a barra é liberada do repouso quand
Resolva o problema 17.25, assumindo que o cilindro é substituído por um tubo de parede fina de raio r e massa m.17.25 - Uma corda é enrolada em torno de um cilindro de raio r e massa m, conforme mostr
As extremidades de uma haste AB de 9 lb são restritas a se mover ao longo de fendas cortadas em uma placa vertical, como mostrado. Uma mola de constante k = 3 l b / i n . é fixado à extremidade A de t
O movimento da haste delgada de 10 kg AB é guiado por colares de massa desprezível que deslizam livremente nas hastes verticais e horizontais mostradas. Sabendo que a barra é solta do repouso quando θ