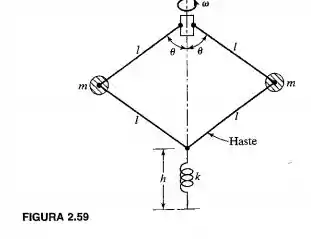
2.29. O diagrama esquemático de um regulador centrífugo é mostrado na figura 2.59. O comprimento de cada haste é l, a massa de cada esfera é m, e o comprimento livre da mola é h. Se a velocidade do eixo for , determine a posição de equilíbrio e a frequência para pequenas oscilações em relação a essa posição.
Passo 1
Beleza, hora de mais uma questão. A primeira coisa que podemos reparar é que quando a altura vertical é . O sistema vai ficar mais ou menos assim:
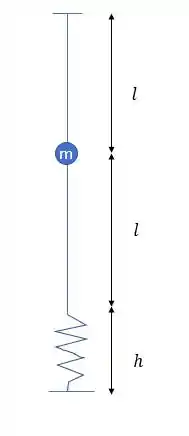
Mas quando a altura vertical é igual a
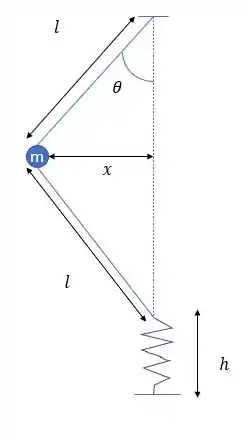
E é
Passo 2
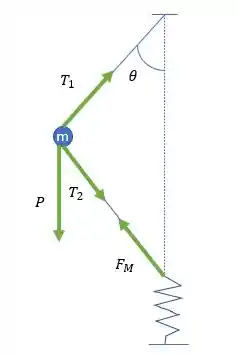
Vamos fazer o diagrama de forças para a massa.
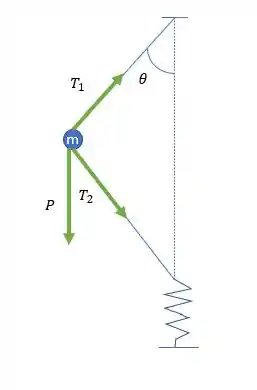
Agora a gente pode escrever as equações de equilíbrio para o sistema. Na vertical fica o seguinte:
Ou então
Agora vamos fazer para o eixo horizontal:
Em que é a força centrípeta.
Vamos isolar dessa última equação:
Agora substituímos isso na equação de equilíbrio vertical
Vamos isolar
Finalmente ficamos com
Podemos assumir
E aí ficamos com
Agora podemos descobrir também o valor de
Isso fica
Passo 3
Vamos parar de fingir que aquela mola não existe, vamos considera-la nas equações.
A força da mola é:
Para o caso do exercício:
Mas olha só, a gente pode assumir que
Basta usar a terceira lei de Newton.
Sabendo disso vamos fazer:
Substituindo o valor de
Agora vamos isolar
Logo
Então
Temos uma equação para . Essa equação pode definir a posição de equilíbrio da massa.
Passo 4
Já fizemos a parte mais difícil. Falta calcular a frequência para pequenas oscilações. Usualmente a gente calcula a frequência assim:
Mas nesse caso teremos duas hastes ligadas a mola, então podemos fazer