2.29. No regulador de Hartnell mostrado na Figura 2.60, a rigidez da mola é , e o peso de cada esfera é 25 N. O comprimento do braço da esfera é 20 cm, e o da manga do braço é 12 cm. A distância entre o eixo de rotação e o ponto da articulação da alavanca angular é 16 cm. A mola é comprimida 1 cm quando o braço da esfera permanece na posição vertical. Determine:
a) a velocidade do regulador na qual o braço da esfera permanece na posição vertical;
b) a frequência natural de vibrações para pequenos deslocamentos em relação à posição vertical dos braços das esferas.
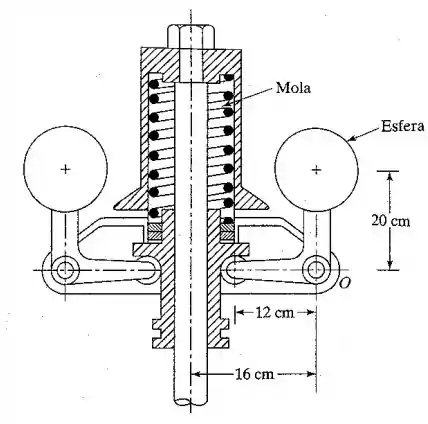
Passo 1
A gente pode começar esse exercício definindo que
A gente pode usar essas forças para fazer a equação de equilíbrio de momento em relação ao ponto O.
Colocando em metros
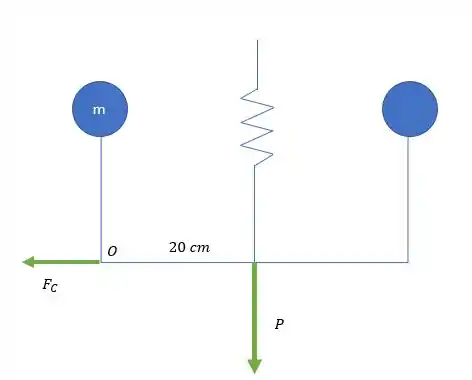
Passo 2
Beleza, agora vamos colocar valores para e .
O exercício nos da , e é a distância da mola em relação ao seu ponto de equilíbrio, ou seja, o quanto a mola foi comprimida, nesse caso foi , ou .
E a força centrifuga fica
Substituindo os valores
Então
Agora que temos os valores das forças, vamos voltar a equação de equilíbrio:
Agora temos tudo para achar
A gente pode converter esse valor para , basta multiplicar por
E assim respondemos o item (a).
Passo 3
Metade do problema já foi! Agora falta o item (b).
Vamos ter um sistema mais ou menos assim:
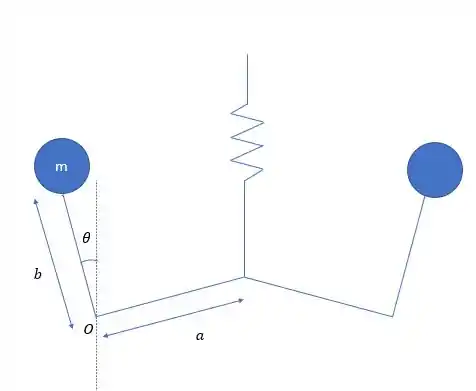
A gente pode usar a equação de movimento sobre o ponto O
Para pequenos valores de podemos fazer as aproximações
E aí ficamos com
Aqui a frequência pode ser calculada assim:
Substituindo os valores
E assim a gente termina outro problema.