Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 31
31- Determine a força exercida na tora por cada garra do pegador de lenha mostrado.
Passo 1
Analisando somente a articulação conseguimos identificar três forças ativas, as forças . Porém as forças e geram deslocamentos virtuais iguais a e e a articulação por consequência tende a baixar num módulo igual a . O que forma o seguinte desenho abaixo.
Onde a barra tende a girar numa velocidade angular que inventamos igual a e a barra numa velocidade angular igual a
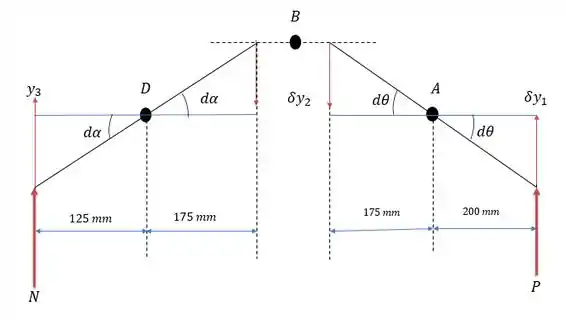
Passo 2
Onde o deslocamento e tendem a formar um ângulo , logo a velocidade linear desses dois deslocamentos serão iguais a:
A velocidade angular é calculada por ou
Dividindo as duas equações temos a seguinte relação:
Analisando agora os deslocamentos de e temos as seguintes velocidades lineares:
O que nos dá uma relação entre e igual a:
Logo, eliminado :
Passo 3
Agora podemos fazer a somatória dos trabalhos ser zero.
Onde tende a andar na direção de e na direção de .
Cortando :
O sinal indica que o vetor foi desenhado ao contrário do real. Isso nos diz que a força real é a força de reação.