Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 25

3.25. Determine o peso máximo do balde que o sistema de fios pode suportar, de modo que nenhum fio desenvolva uma tração maior que 0,5   k N .

Passo 1

Falaa! Então, ele quer o maio peso do balde para que a tração nos cabos não ultrapasse 0,5   k N .

Digamos que o peso do balde seja P . O que a gente vai fazer é achar todas as trações em função de P , descobrir qual é a maior delas, e forçar que ela seja menor que 0,5   k N , aí isso vai valer para todas as outras e achamos P .

Para resolver esse exercício usaremos as equações de equilíbrio nos eixos x e y. Primeiro faremos isso para o ponto E da figura.

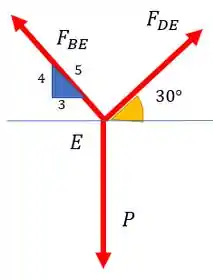
Depois disso faremos a mesma coisa para o ponto B na figura.

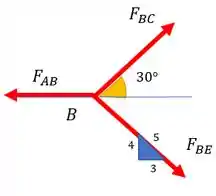
Bora!

Passo 2

Vamos começar calculando F R x no ponto E.

F R x = 0

Primeiro repare nesse triângulo

Por definição

cos ⁡ α = 3 5

sin ⁡ α = 4 5

Assim:

F R x = F E D ⋅ cos ⁡ 30 ° - F E B ⋅ cos ⁡ α = F E D ⋅ cos ⁡ 30 ° - F E B ⋅ cos ⁡ α = 0

F R x = F E D ⋅ cos ⁡ 30 ° - F E B ⋅ cos ⁡ α = F E D ⋅ cos ⁡ 30 ° - F E B ⋅ 3 5 = 0

Então

Agora vamos fazer o mesmo para F R y

F R y = 0

F R y = F E D ⋅ sin ⁡ 30 ° + F E B ⋅ sin ⁡ α - P = F E D ⋅ sin ⁡ 30 ° + F E B ⋅ s e n   α - P = 0

F R y = F E D ⋅ sin ⁡ 30 ° + F E B ⋅ sin ⁡ α - P = F E D ⋅ sin ⁡ 30 ° + F E B ⋅ 4 5 - P = 0

Passo 3

Agora temos duas incógnitas e duas equações, vamos resolva-las.

F E D ⋅ cos ⁡ 30 ° - F E B ⋅ 3 5 = F E D ⋅ sin ⁡ 30 ° + F E B ⋅ 4 5 - P

Vamos isolar F E D

F E D ⋅ cos ⁡ 30 ° - F E D ⋅ sin ⁡ 30 ° = F E B ⋅ 3 5 + F E B ⋅ 4 5 - P

F E D = F E B ⋅ 3 5 + 4 5 - P cos ⁡ 30 ° - sin ⁡ 30 ° = F E B ⋅ 7 5 - P 0,366

Agora podemos substituir em uma das equações

F E D ⋅ cos ⁡ 30 ° - F E B ⋅ 3 5 = 0

F E B ⋅ 7 5 - P 0,366 ⋅ cos ⁡ 30 ° - F E B ⋅ 3 5 = 0

F E B ⋅ 7 5 0,366 ⋅ cos ⁡ 30 ° - F E B ⋅ 3 5 = P 0,366 ⋅ cos ⁡ 30 °

F E B ⋅ 7 5 0,366 ⋅ cos ⁡ 30 ° - 3 5 = P ⋅ cos ⁡ 30 ° 0,366

F E B = P ⋅ cos ⁡ 30 ° 0,366 7 5 0,366 ⋅ cos ⁡ 30 ° - 3 5 = 0,8723 P

Passo 4

Agora com F E B podemos determina F E D

F E D ⋅ sin ⁡ 30 ° + 0,8723 P ⋅ 4 5 - P = 0

F E D ⋅ sin ⁡ 30 ° = P - 0,8723 P ⋅ 4 5

F E D = P ⋅ 1 - 0,8723 ⋅ 4 5 sin ⁡ 30 ° = 0,6043 P

Passo 5

Agora vamos usar a equação de equilíbrio no ponto B

F R y = 0

F R y = F B C ⋅ sin ⁡ 30 ° - F E B ⋅ s e n   α = 0

F R y = F B C ⋅ sin ⁡ 30 ° - F E B ⋅ 4 5 = 0

Então

F B C ⋅ sin ⁡ 30 ° = F E B ⋅ 4 5

F B C = F E B ⋅ 4 5 sin ⁡ 30 ° = 1,3957 P

Agora o eixo x

F R x = 0

F R x = F B C ⋅ cos ⁡ 30 ° + F E B ⋅ cos ⁡ α - F B A = 0

F R x = F B C ⋅ cos ⁡ 30 ° + F E B ⋅ 3 5 - F B A = 0

Vamos isolar F B A

F B A = F B C ⋅ cos ⁡ 30 ° + F E B ⋅ 3 5 = 1,7320 P

Passo 6

Note que F B A é maior do que todas as outras forças, então se F B A for menor que 0,5   k N todas as outras forças também serão consequentemente, logo

F B A = 0,5 k N = 500   N

1,7320 P = 500

P = 500 1,7320 = 288,68   N

Portanto, o maior peso que o balde pode ter é de 288,68 N

Resposta

P = 288,68   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para facilitar a mudança de posição de um gancho para levantar carga quando ele está descarregado, usa-se o suporte deslizante mostrado. Os ressaltos em A e B se prendem aos flanges de uma viga caixão
Em um procedimento para avaliar a resistência do músculo tríceps, uma pessoa força para baixo uma célula de carga com a palma da mão, como mostrado na figura. Se a leitura da célula de carga é de 160N
O conector de correntes é utilizado para segurar cargas de troncos, madeira, tubos e congêneres. Se a força trativa T 1 vale 2k N quando θ = 30 ° , determine a força P necessária na alavanca e a força
O dispositivo mostrado é projetado para aplicar pressão dos dois lados de uma bancada, durante a colagem do laminado próximo à borda. Se uma força de 120N é aplicada à barra, determine a força que cad
Para comprovar a validade das hipóteses aerodinâmicas feitas no projeto de um avião, seu modelo está sendo testado em um túnel de vento. O suporte está conectado a um dispositivo para equilibrar força