Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 16

Determine as reações normais em A e B e a força na ligação CD agindo sobre o membro no problema 8

Passo 1

Bem Vamos relembrar que questão é essa?

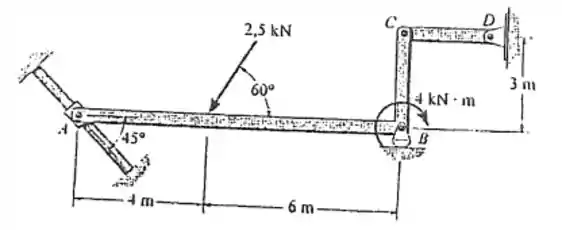
Vamos aproveitar e dar uma olhada no diagrama de forças

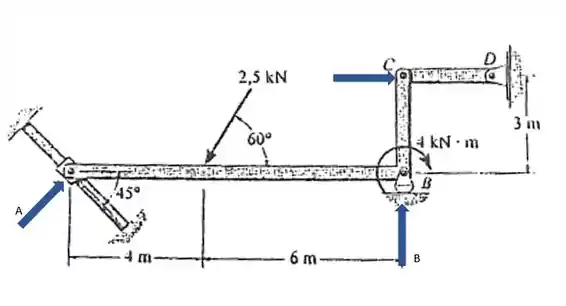
Tinha essa peça ABC apoiada numa haste lisa em A e um rolete em B. E uma ligação curta em CD.

Passo 2

Bem estamos em equilíbrio então As forças verticais, horizontais e Momentos binários se anulam

Vamos definir uma Orientação antes de começar. Gosto sempre de trabalhar em sentido horário. Essa orientação é arbitrária, se você estiver feito no sentido contrário, beleza! Só ao conferir as contas os sinais estarão trocados.

Então vamos lá. Tudo o que fizer meu sistema tentar rodar em Horario é ( + ), tudo o que tentar fazer tentar rodar em sentido contrario é ( - ) .

Outra coisa. Quando fazemos momento Binário temos que olhar para o PAR distancia e força. Elas têm que ser ortogonais. Show! Vamos cair dentro.

Passo 3

Vamos fazer o momento binário do sistema. Vou escolher o ponto B como ponto de partida

Vou unir a duas equações de C

Logo

E também

Prontinho 😊

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

É desejável que uma pessoa seja capaz de iniciar o fechamento da porta do bagageiro de uma van, desde a posição aberta mostrada, com uma força vertical P de 40N . Como um exercício de projeto, determi

Para testar a deflexão da viga uniforme de 100k g , o garoto de 50k g dá um puxão de 150N na corda, como mostrado. Calcule a força suportada pelo pino na dobradiça O .

Determine as reações externas em A e F para a treliça de um telhado carregada como mostrado. As cargas verticais representam o efeito de sustentação dos materiais do telhado, enquanto a força de 400N

O carro completo, com seu motorista, tem massa de 815k g e, sem os dois aerofólios, tem uma distribuição de peso igual ( 50 % - 50 % ) entre a dianteira e a traseira em uma dada velocidade na qual o c

O elemento O B C e a roldana em C , juntos, têm uma massa de 500k g , com um centro de massa combinado em G . Calcule o módulo da força suportada pela conexão de pino em O quando a carga de 3k N é apl