Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.4 - Ex. 49
49- U m pequeno elevador industrial, acionado a pedal, está mostrado na figura. Existem quatro molas idênticas, duas de cada lado do eixo central. A rigidez de cada par de molas vale . Ao projetar o elevador, especifique o valor de , que assegurará equilíbrio estável quando o elevador suporta uma carga (peso) na posição para a qual , sem qualquer força sobre o pedal. Pode-se considerar que as molas atuam sempre na direção horizontal e, inicialmente, estão pré-comprimidas.
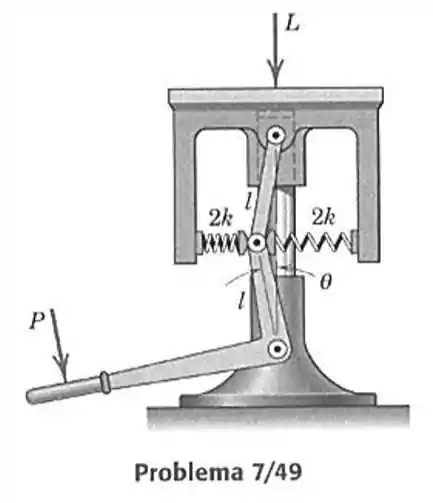
Passo 1
Como não temos a força agindo no sistema então não temos trabalho causado por essa força, além de considerarmos que as molas estão comprimidas inicialmente de um valor .
Agora fazendo o desenho do sistema de forças nós temos:
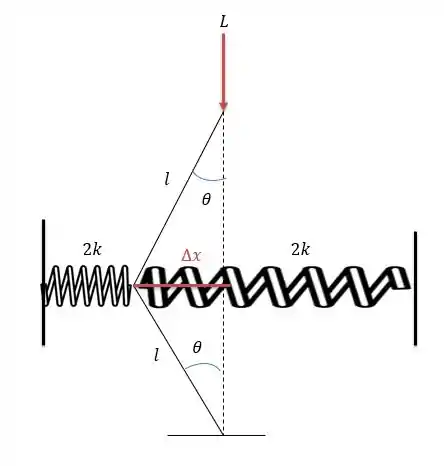
Como não é falado de nenhuma massa nas barras de comprimento então considera-se que as barras suportam a carga de e seu centro de carga será calculado da mesma forma que foi feita na questão , logo a energia potencial desse sistema será de:
E para a energia elástica potencial elástica temos:
Onde é calculado fazendo o seno de , e como uma mola estica em uma proporção a outra mola contrai-se com a mesma intensidade.
O que nos dá uma energia total igual a:
Passo 2
Derivando a energia em relação a nós teremos:
Como nós podemos escrever essa equação da seguinte forma:
O que nos mostra que se fizermos será uma posição de equilíbrio.
Agora derivando de novo essa equação nós teremos:
Passo 3
Para o sistema ser estável em nós fazemos:
Isolando nós encontraremos o valor da constante elástica que nos deixará com o sistema estável: