Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 50

Determine a coordenada y do centroide da área sombreada. O triângulo é equilátero.

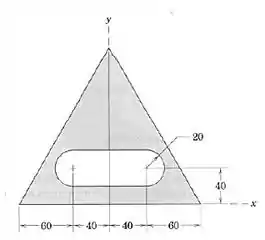
Passo 1

Sabendo que aa equação para encontrar o centro de massa é dado por:

  y - =   ∑ y - A ∑ A  

Dessa maneira, vamos primeiro encontrar os centros de cada parte.

Passo 2

Mas antes vamos separar cada componente, de tal modo que:

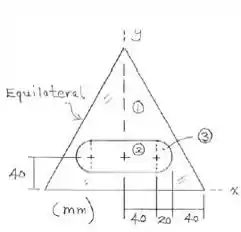
Pronto! Escolhido os componentes vamos montar uma tabela com cada parte

Passo 3

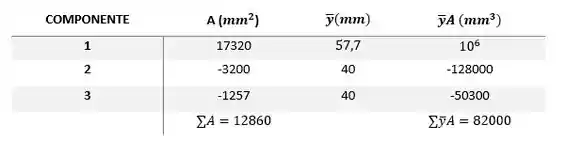
No primeiro componente, vemos que a área de um triângulo equilátero é dada por:

A t = l 2 3 4 = 200 2 3 4 = 173200 m m 2

Com isso, e sabendo que o centroide do triângulo é um terço da altura temos:

y - t = 1 3 h = 1 3 l 3 2 = 1 3 200 3 2 = 57,7 m m  

Já no segundo componente, que é um retângulo, temos que a área é

A r = 2 * 40 * 40 = 3200 m m 2

E o centroide fica no meio, logo, como relação a origem temos:

y r - = 40 m m

Já o terceiro componente é um semiciclo, ou seja, a área é dada por:

A s = 1 2 π r 2 = 1 2 π 20 2 = 628

Como são dois, temos:

2 A s = 1257 m m 2

Note que o centroide do semiciclo é o mesmo do retângulo, logo

y - s = 40 m m

Passo 4

Agora só basta substituir na equação que teremos nosso ponto:

y - =   ∑ y - A ∑ A = 822000 12860 = 63,9   m m

Resposta

  y - = 63,9   m m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os dois segmentos superiores do conjunto de barras esbeltas uniformes, soldadas em Y, tem uma massa por unidade de comprimento de 0,3k g / m , enquanto o segmento inferior tem uma massa de 0,5k g / m
Determine a distancia H - desde o fundo da placa da base até o centroide da seção estrutural mostrada.
Determine a coordenada x do centro de massa do suporte construído com uma placa uniforme de aço.
O conjunto rigidamente unido consiste em um disco circular de 2kg, um eixo redondo de 1,5kg e uma placa quadrada de 1kg. Determine a coordenada z do centro de massa do conjunto.
O hemisfério homogêneo do problema 5/42, cuja porção hemisférica central foi removida, está repetido aqui. Determine a coordenada x do centro de massa usando o método desta seção.