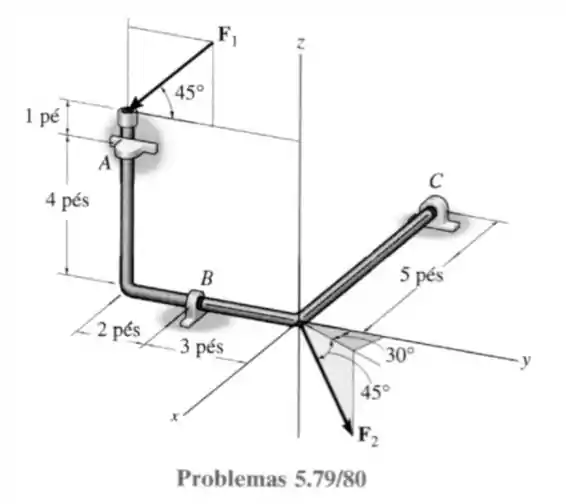
79- A barra dobrada é apoiada em e por mancais simples. Calcule os componentes de reação nos mancais quando a barra está sujeita as forças e . se localiza no plano . Os mancais estão alinhados e exercem apenas forças reativas sobre a barra.
Passo 1
Temos três apoios, em , e e são apoios que oferecem resistências a forças em somente dois eixos (eixos onde a barra não consegue se mover livremente), isso é os apoios oferecem resistências em:
E como a força está no plano então decompondo essa força temos a seguinte representação vetorial:
E a projeção de será:
E o diagrama de forças será igual a:
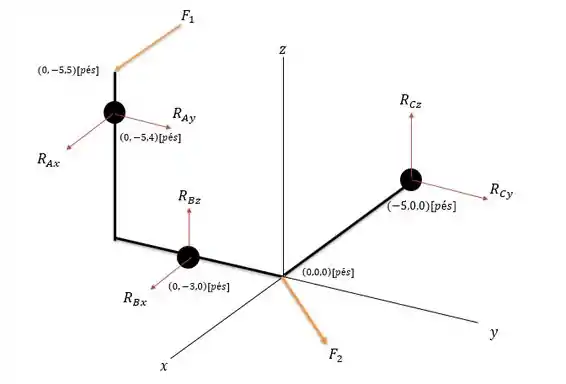
Passo 2
Vamos fazer a somatória das forças em e igualar-la a zero:
Agora vamos fazer a somatória das forças em :
E a somatória das forças em :
Passo 3
Agora para a somatória dos momentos, vamos escolher a somatória dos momentos na origem, onde se encontra a força .
Para a somatória dos momentos em temos que pegar as distâncias (positivas ou negativas a origem) em ou em com as forças em e .
Agora a somatória dos momentos em , distâncias em com forças em ou distâncias em com forças em .
Agora a somatória dos momento em , temos que pegar as forças em com as distâncias em ou as forças em com as distâncias em .
Passo 4
Temos seis equações para seis incógnitas podemos resolver todas elas, vamos organizar todas elas.
Do sistema conseguimos ver que aparece mais vezes, tendo até uma correlação sem número com . Então elas será a variável intermediária do sistema, começando por temos:
Aplicando esse resultado em temos:
A equação então ficará:
A equação então fica:
A equação podendo ser escrita por:
Agora substituindo os valores de e em função de na equação nos dará:
Agora só resolver todas as forças.