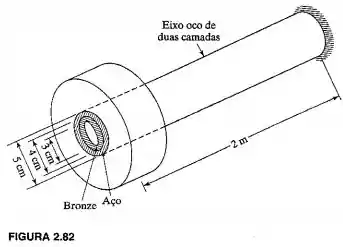
Um anel pesado de momento de inércia de massa está ligado à extremidade de um eixo oco de duas camadas de 2 m de comprimento (Figura 2.82). Se as duas camadas do eixo forem feitas de aço e bronze, determine o período natural de vibração torcional do anel pesado.
Passo 1
Vamos calcular o momento polar de inércia do eixo para a seção transversal do aço:
Substituindo os valores, temos que:
Vamos fazer o mesmo procedimento para calcular o momento de inércia do latão:
Passo 2
A rigidez torcional da parte de aço é dada por:
Substituindo os valores, temos que:
Para o latão, temos que:
A rigidez equivalente do sistema será:
Passo 3
Sabendo que a frequência natural de vibração do sistema pode ser dada por:
Temos que:
O período de tempo natural de vibração de torção do anel é dado por:
Substituindo os valores, temos que: