A barra uniforme de e massa de é articulada em e impedida de girar mais do que no plano vertical pelo rolete fixo em . Calcule o módulo da força total suportada pelo pino em .

Passo 1
Primeiro vamos definir os eixos e desenhar as forças que agem sobre a barra:
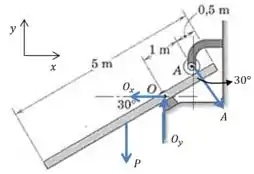
Não se preocupe demais com o sentido das forças em cada ponto (no desenho), se você errar o sentido real da força no desenho, o valor associado a ela vai simplesmente aparecer com um sinal negativo no final.
Vamos começar pelo mais simples: aplicar a condição de equilíbrio das forças em cada direção:
E então ficamos com as seguintes expressões para as componentes de :
E então só falta calcular o valor de .
Passo 2
Vamos aplicar mais uma equação de equilíbrio: a dos momentos em torno do ponto . Nesse caso as forças e têm momento nulo, e ficamos só com a componente do peso que é perpendicular à barra, e com a força , que já é perpendicular.
Só precisamos multiplicar cada uma dessas forças pela distância dos seus pontos de aplicação até o ponto :
E agora é só substituir no sistema que encontramos lá em cima:
E então o módulo da força é:
Resposta
O módulo da força é .