Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 86
O corpo mostrado em seção transversal é um anel circular completo formado pela rotação da área octogonal em torno do eixo z. Toda a superfície deve ser coberta com um revestimento especial. Determine esta área de superfície.
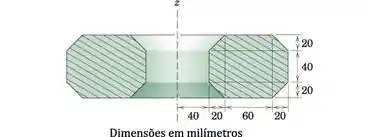
Passo 1
Lembre-se dos teoremas de Pappus que a superfície externa de um corpo pode ser encontrada pela fórmula:
E o Volume pode ser encontrado pela fórmula:
representa a distância do centro de massa do eixo de revolução
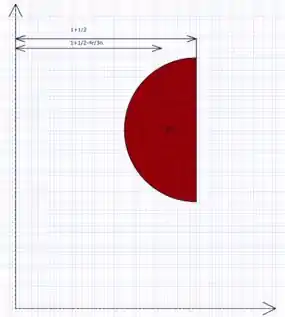
Este problema é realmente fácil de resolver. Primeiro, olhamos para o Problema Amostra 5/3, a partir do qual sabemos que o centro de massa de um semicírculo é:
Passo 2
No entanto, o resultado do Problema Resolvido 5/3 é em relação ao centro do círculo. Precisamos disso em relação ao eixo vertical. Então, fazendo esses ajustes conforme mostrado na figura:
Já a Área é a metade de um círculo completo com o mesmo raio, então:
Passo 3
Em seguida, precisamos encontrar , uma vez que a revolução é 360, escrevemos:
Finalmente, estamos procurando encontrar o Volume aqui, então usaremos a segunda fórmula do Teorema de Pappus:
Usando isso, escrevemos:
Passo 4
Para encontrar a área da superfície, precisamos apenas dividir as linhas em L1 e L2, conforme mostrado na figura. O centro de massa para L1 pode ser encontrado usando o Problema de Amostra 5/1:
No entanto, o resultado do Problema Resolvido 5/1 é em relação ao centro do círculo. Precisamos disso em relação ao eixo vertical. Então, fazendo esses ajustes conforme mostrado na figura:
Passo 5
O comprimento de L1 é o de um semicírculo, então:
Quanto à distância entre o centro de massa de L2 e o eixo vertical e o comprimento de L2 é bastante simples:
Passo 6
Finalmente, estamos procurando encontrar a Área da superfície aqui, então usaremos a primeira fórmula do Teorema de Pappus:
Usando isso, escrevemos: