Derive a expressão para a frequência natural do sistema mostrado na figura. Observe que a carga W é aplicada na extremidade da viga 1 e no ponto médio da viga 2.
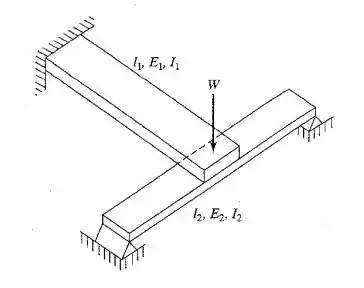
Passo 1
Vamos lá resolver mais essa. A constante elástica da viga 1, considerando que a carga é aplicada na extremidade da viga é dada por:
Para a viga 2, essa constante, considerando que a carga é aplicada no seu ponto médio, é dada por:
Passo 2
A constante elástica equivalente é calculada como:
Assim, a frequência natural é dada por: